优化算法笔记（八）人工蜂群算法

Posted 2023-04-06

参考技术A （以下描述，均不是学术用语，仅供大家快乐的阅读）
　　工蜂群算法（Artificial Bee Colony Algorithm，ABC）是一种模仿蜜蜂采蜜机理而产生的群智能优化算法。其原理相对复杂，但实现较为简单，在许多领域中都有研究和应用。
　　人工蜂群算法中，每一个蜜源的位置代表了待求问题的一个可行解。蜂群分为采蜜蜂、观察蜂和侦查蜂。采蜜蜂与蜜源对应，一个采蜜蜂对应一个蜜源。观察蜂则会根据采蜜蜂分享的蜜源相关信息选择跟随哪个采蜜蜂去相应的蜜源，同时该观察蜂将转变为侦查蜂。侦查蜂则自由的搜索新的蜜源。每一个蜜源都有开采的限制次数，当一个蜜源被采蜜多次而达到开采限制次数时，在该蜜源采蜜的采蜜蜂将转变为侦查蜂。每个侦查蜂将随机寻找一个新蜜源进行开采，并转变成为采蜜蜂。

下面是我的实现方式（我的答案）：
　　1． 三种蜜蜂之间可以相互转化。
　　采蜜蜂->观察蜂：有观察蜂在采蜜过程中发现了比当前采蜜蜂更好的蜜源，则采蜜蜂放弃当前蜜源转而变成观察蜂跟随优质蜜源，同时该观察蜂转变为采蜜蜂。
　　采蜜蜂->观察蜂：当该采蜜蜂所发现的蜜源被开采完后，它会转变为观察蜂去跟随其他采蜜蜂。
　　采蜜蜂->侦查蜂：当所有的采蜜蜂发现的蜜源都被开采完后，采蜜蜂将会变为侦查蜂，观察蜂也会变成侦查蜂，因为大家都无蜜可采。
　　侦查蜂->采蜜蜂、观察蜂：侦查蜂随机搜索蜜源，选择较好的数个蜜源位置的蜜蜂为采蜜蜂，其他蜜蜂为观察蜂。

　　2.蜜源的数量上限
　　蜜源的数量上限等于采蜜蜂的数量上限。初始化时所有蜜蜂都是侦查蜂，在这些侦查蜂所搜索到的蜜源中选出数个较优的蜜源，发现这些蜜源的侦查蜂变为采蜜蜂，其他蜜蜂变为观察蜂。直到所有的蜜源都被开采完之前，蜜源的数量不会增加，因为这个过程中没有产生侦查蜂。所有的蜜源都被开采完后，所有的蜜蜂再次全部转化为侦查蜂，新的一轮蜜源搜索开始。也可以在一个蜜源开采完时马上产生一个新的蜜源补充，保证在整个开采过程中蜜源数量恒定不变。

蜜源的开采实际上就是观察蜂跟随采蜜蜂飞向蜜源的过程。得到的下一代的位置公式如下：

表示第i只观察蜂在第t代时随机选择第r只采蜜蜂飞行一段距离，其中R为（-1，1）的随机数。

一只观察蜂在一次迭代过程中只能选择一只采蜜蜂跟随，它需要从众多的采蜜蜂中选择一只来进行跟随。观察蜂选择的策略很简单，随机跟随一只采蜜蜂，该采蜜蜂发现的蜜源越优，则选择它的概率越大。
　　是不是很像轮盘赌，对，这就是轮盘赌，同时我们也可以稍作修改，比如将勤劳的小蜜蜂改为懒惰的小蜜蜂，小蜜蜂会根据蜜源的优劣和距离以及开采程度等因素综合来选择跟随哪只采蜜蜂（虽然影响不大，但聊胜于无）。
　　忘记了轮盘赌的小伙伴可以看一下 优化算法笔记（六）遗传算法 。
　　下面是我的人工蜂群算法流程图

又到了实验环节，参数实验较多，全部给出将会占用太多篇幅，仅将结果进行汇总展示。

实验1：参数如下

　　上图分别为采蜜蜂上限为10%总数和50%总数的情况，可以看出当采蜜蜂上限为10%总群数时，种群收敛的速度较快，但是到最后有一个点死活不动，这是因为该点作为一个蜜源，但由于适应度值太差，使用轮盘赌被选择到的概率太小从而没有得到更佳的蜜源位置，而因未开采完，采蜜蜂又不能放弃该蜜源。
　　看了看采蜜蜂上限为50%总群数时的图，发现也有几个点不动的状态，可以看出，这时不动的点的数量明显多于上限为10%总数的图，原因很简单，采蜜蜂太多，“先富”的人太多，而“后富”的人较少，没有带动“后富者”的“先富者”也得不到发展。
　　看看结果

嗯，感觉结果并没有什么差别，可能由于问题较简单，迭代次数较少，无法体现出采蜜蜂数对于结果的影响，也可能由于蜜源的搜索次数为60较大，总群一共只能对最多20*50/60=16个蜜源进行搜索。我们将最大迭代次数调大至200代再看看结果

当最大迭代次数为200时，人工蜂群算法的结果如上图，我们可以明显的看出，随着采蜜蜂上限的上升，算法结果的精度在不断的下降，这也印证了之前的结果，由于蜜源搜索次数较大（即搜索深度较深）采蜜蜂数量越多（搜索广度越多），结果的精度越低。不过影响也不算太大，下面我们再来看看蜜源最大开采次数对结果的影响。
实验2：参数如下

上图分别是蜜源开采限度为1,20和4000的实验。
　　当蜜源开采上限为1时，即一个蜜源只能被开采一次，即此时的人工蜂群算法只有侦查蜂随机搜索的过程，没有观察蜂跟随采蜜蜂的过程，可以看出图中的蜜蜂一直在不断的随机出现在新位置不会向某个点收敛。
　　当蜜源开采上限为20时，我们可以看到此时种群中的蜜蜂都会向一个点飞行。在一段时间内，有数个点一动不动，这些点可能就是采蜜蜂发现的位置不怎么好的蜜源，但是在几次迭代之后，它们仍会被观察蜂开采，从而更新位置，蜜源开采上限越高，它们停顿的代数也会越长。在所有蜜蜂都收敛于一个点之后，我们可以看到仍会不断的出现其他的随机点，这些点是侦查蜂进行随机搜索产生的新的蜜源位置，这些是人工蜂群算法跳出局部最优能力的体现。
当蜜源开采上限为4000时，即不会出现侦查蜂的搜索过程，观察蜂只会开采初始化时出现的蜜源而不会采蜜蜂不会有新的蜜源产生，可以看出在蜂群收敛后没有出现新的蜜源位置。

看看最终结果，我们发现，当蜜源开采上线大于1时的结果提升，但是好像开采上限为5时结果明显好于开采次数上限为其他的结果，而且随着开采次数不断上升，结果在不断的变差。为什么会出现这样的结果呢？原因可能还是因为问题较为简单，在5次开采的限度内，观察蜂已经能找到更好的蜜源进行开采，当问题较为复杂时，我们无法知晓开采发现新蜜源的难度，蜜源开采上限应该取一个相对较大的值。当蜜源开采限度为4000时,即一个蜜源不可能被开采完(开采次数为20(种群数)*200(迭代次数)),搜索的深度有了但是其结果反而不如开采限度为几次几十次来的好,而且这样不会有侦查蜂随机搜索的过程,失去了跳出局部最优的能力。
　　我们应该如何选择蜜源的最大开采次数限制呢？其实，没有最佳的开采次数限制，当适应度函数较为简单时，开采次数较小时能得到比较好的结果，但是适应度函数较复杂时，经过试验，得出的结果远差于开采次数较大时。当然，前面就说过，适应度函数是一个黑盒模型，我们无法判断问题的难易。那么我们应该选择一个适中的值，个人的选择是种群数的0.5倍到总群数的2倍作为蜜源的最大开采次数，这样可以保证极端情况下，1-2个迭代周期内小蜜蜂们能将一个蜜源开采完。

人工蜂群算法算是一个困扰我比较长时间的算法，几年时间里，我根据文献实现的人工蜂群算法都有数十种，只能说人工蜂群算法的描述太过模糊，或者说太过抽象，研究者怎么实现都说的通。但是通过实现多次之后发现虽然实现细节大不相同，但效果相差不多，所以我们可以认为人工蜂群算法的稳定性比较强，只要实现其主要思想即可，细节对于结果的影响不太大。
　　对于人工蜂群算法影响最大的因素还是蜜源的开采次数限制，开采次数限制越大，对同一蜜源的开发力度越大，但是分配给其他蜜源的搜索力度会相对减少，也会降低蜂群算法的跳出局部最优能力。可以动态修改蜜源的开采次数限制来实现对算法的改进，不过效果不显著。
　　其次对于人工蜂群算法影响是三类蜜蜂的搜索行为，我们可以重新设计蜂群的搜索方式来对算法进行改进，比如采蜜蜂在开采蜜源时是随机飞向其他蜜源，而观察蜂向所选的蜜源靠近。这样改进有一定效果但是在高维问题上效果仍不明显。
　　以下指标纯属个人yy,仅供参考

目录
上一篇 优化算法笔记（七）差分进化算法
下一篇 优化算法笔记（九）杜鹃搜索算法

优化算法matlab实现（八）人工蜂群算法matlab实现

优化求解人工蜂群ABC算法

​一、人工蜂群算法的介绍

    人工蜂群算法(Artificial Bee Colony, ABC)是由Karaboga于2005年提出的一种新颖的基于群智能的全局优化算法，其直观背景来源于蜂群的采蜜行为，蜜蜂根据各自的分工进行不同的活动，并实现蜂群信息的共享和交流，从而找到问题的最优解。人工蜂群算法属于群智能算法的一种。

二、人工蜂群算法的原理

   1、原理

        标准的ABC算法通过模拟实际蜜蜂的采蜜机制将人工蜂群分为3类: 采蜜蜂、观察蜂和侦察蜂。整个蜂群的目标是寻找花蜜量最大的蜜源。在标准的ABC算法中，采蜜蜂利用先前的蜜源信息寻找新的蜜源并与观察蜂分享蜜源信息；观察蜂在蜂房中等待并依据采蜜蜂分享的信息寻找新的蜜源；侦查蜂的任务是寻找一个新的有价值的蜜源，它们在蜂房附近随机地寻找蜜源。

        假设问题的解空间是D维的，采蜜蜂与观察蜂的个数都是SN，采蜜蜂的个数或观察蜂的个数与蜜源的数量相等。则标准的ABC算法将优化问题的求解过程看成是在D维搜索空间中进行搜索。每个蜜源的位置代表问题的一个可能解，蜜源的花蜜量对应于相应的解的适应度。一个采蜜蜂与一个蜜源是相对应的。与第i个蜜源相对应的采蜜蜂依据如下公式寻找新的蜜源：

 

 

 其中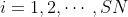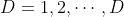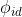，，，，是区间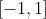上的随机数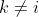，。标准的ABC算法将新生成的可能解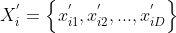与原来的解作比较，并采用贪婪选择策略保留较好的解。每一个观察蜂依据概率选择一个蜜源，概率公式为

其中，是可能解的适应值。对于被选择的蜜源，观察蜂根据上面概率公式搜寻新的可能解。当所有的采蜜蜂和观察蜂都搜索完整个搜索空间时，如果一个蜜源的适应值在给定的步骤内(定义为控制参数“limit”) 没有被提高, 则丢弃该蜜源，而与该蜜源相对应的采蜜蜂变成侦查蜂，侦查蜂通过已下公式搜索新的可能解。

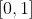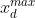其中，是区间上的随机数，和是第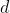维的下界和上界。

  2、流程

• 初始化；

• 重复以下过程：

  • 将采蜜蜂与蜜源一一对应，根据上面第一个公式更新蜜源信息，同时确定蜜源的花蜜量；

  • 观察蜂根据采蜜蜂所提供的信息采用一定的选择策略选择蜜源，根据第一个公式更新蜜源信息，同时确定蜜源的花蜜量；

  • 确定侦查蜂，并根据第三个公式寻找新的蜜源；

  • 记忆迄今为止最好的蜜源；

• 判断终止条件是否成立；

三、人工蜂群算法用于求解函数优化问题

    对于函数

其中。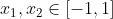

%% Copyright (c) 2015, Yarpiz (www.yarpiz.com)% All rights reserved. Please read the "license.txt" for license terms.%% Project Code: YPEA114% Project Title: Implementation of Artificial Bee Colony in MATLAB% Publisher: Yarpiz (www.yarpiz.com)% % Developer: S. Mostapha Kalami Heris (Member of Yarpiz Team)% % Contact Info: [e-mail], [e-mail]%​clc;clear;close all;​%% Problem Definition​CostFunction=@(x) Sphere(x);        % Cost Function​nVar=5;             % Number of Decision Variables​VarSize=[1 nVar];   % Decision Variables Matrix Size​VarMin=-10;         % Decision Variables Lower BoundVarMax= 10;         % Decision Variables Upper Bound​%% ABC Settings​MaxIt=200;              % Maximum Number of Iterations​nPop=100;               % Population Size (Colony Size)​nOnlooker=nPop;         % Number of Onlooker Bees​L=round(0.6*nVar*nPop); % Abandonment Limit Parameter (Trial Limit)​a=1;                    % Acceleration Coefficient Upper Bound​%% Initialization​% Empty Bee Structureempty_bee.Position=[];empty_bee.Cost=[];​% Initialize Population Arraypop=repmat(empty_bee,nPop,1);​% Initialize Best Solution Ever FoundBestSol.Cost=inf;​% Create Initial Populationfor i=1:nPop    pop(i).Position=unifrnd(VarMin,VarMax,VarSize);    pop(i).Cost=CostFunction(pop(i).Position);    if pop(i).Cost<=BestSol.Cost        BestSol=pop(i);    endend​% Abandonment CounterC=zeros(nPop,1);​% Array to Hold Best Cost ValuesBestCost=zeros(MaxIt,1);​%% ABC Main Loop​for it=1:MaxIt        % Recruited Bees    for i=1:nPop                % Choose k randomly, not equal to i        K=[1:i-1 i+1:nPop];        k=K(randi([1 numel(K)]));                % Define Acceleration Coeff.        phi=a*unifrnd(-1,+1,VarSize);                % New Bee Position        newbee.Position=pop(i).Position+phi.*(pop(i).Position-pop(k).Position);                % Evaluation        newbee.Cost=CostFunction(newbee.Position);                % Comparision        if newbee.Cost<=pop(i).Cost            pop(i)=newbee;        else            C(i)=C(i)+1;        end            end        % Calculate Fitness Values and Selection Probabilities    F=zeros(nPop,1);    MeanCost = mean([pop.Cost]);    for i=1:nPop        F(i) = exp(-pop(i).Cost/MeanCost); % Convert Cost to Fitness    end    P=F/sum(F);        % Onlooker Bees    for m=1:nOnlooker                % Select Source Site        i=RouletteWheelSelection(P);                % Choose k randomly, not equal to i        K=[1:i-1 i+1:nPop];        k=K(randi([1 numel(K)]));                % Define Acceleration Coeff.        phi=a*unifrnd(-1,+1,VarSize);                % New Bee Position        newbee.Position=pop(i).Position+phi.*(pop(i).Position-pop(k).Position);                % Evaluation        newbee.Cost=CostFunction(newbee.Position);                % Comparision        if newbee.Cost<=pop(i).Cost            pop(i)=newbee;        else            C(i)=C(i)+1;        end            end        % Scout Bees    for i=1:nPop        if C(i)>=L            pop(i).Position=unifrnd(VarMin,VarMax,VarSize);            pop(i).Cost=CostFunction(pop(i).Position);            C(i)=0;        end    end        % Update Best Solution Ever Found    for i=1:nPop        if pop(i).Cost<=BestSol.Cost            BestSol=pop(i);        end    end        % Store Best Cost Ever Found    BestCost(it)=BestSol.Cost;        % Display Iteration Information    disp(['Iteration ' num2str(it) ': Best Cost = ' num2str(BestCost(it))]);    end    %% Results​figure;%plot(BestCost,'LineWidth',2);semilogy(BestCost,'LineWidth',2);xlabel('Iteration');ylabel('Best Cost');grid on;​

function [SX0]=observe(Q,Lmin,Lmax)%生成的S1为  population行*C列%但是要保证生成的阈值第一个比后一个小，且不能为图像的最大、小灰度值global population C;P=zeros(8*C,1);w=[1,2,4,8,16,32,64,128];SX0=zeros(population,C);num=3;flag=1;i=1;ill=0; while i<=population         R=rand(8*C,1);                  P(:,1)=R(:,1)>=(Q(:,1,i).^2);             k=1;             while k<=C                     t=(k-1)*8+1;                                SX0(i,k)=w(1,:)*double(P(t:t+7,1));                          temp=1;                   while (SX0(i,k)<=Lmin || SX0(i,k)>=Lmax || ((k>1) && SX0(i,k)<=SX0(i,k-1))) && (temp<=num)                        Rt=rand(8,1);                               P(t:t+7,1)=Rt(:,1)>=(Q(t:t+7,1,i).^2);                                  SX0(i,k)=w(1,:)*double(P(t:t+7,1));                           temp=temp+1;                                            end                                   if (temp>num) && (SX0(i,k)<=Lmin || SX0(i,k)>=Lmax || ((k>1) && SX0(i,k)<=SX0(i,k-1)))                           flag=0;  %表示此组数据不合理                          ill=ill+1;                          R=rand(8*C,1);                                                      P(:,1)=R(:,1)>=(Q(:,1,i).^2);       %有时会出现停滞状态，由于此处的Q的artha==1                          k=1;                   else                        flag=1;                         ill=0;                        k=k+1;                   end                     if ill>=3                                   Q(:,:,i)=ones(8*C,2,1)/sqrt(2);                   end                                 end     %% while k<=C                 i=i+1; end​% % fid = fopen('data.txt', 'wt');% %   for j=1:C% %       for i=1:population% %   % % fprintf(fid, ' %4.0f  ',SX0(i,j));% %         if i==population% %         fprintf(fid, '\\n');% %         end% %   end% % % % fwrite(fid,SX0(:,j),'integer*population');% % % % fwrite(fid,'\\n','char');% % % % end% % fclose(fid);​

​function i=RouletteWheelSelection(P)​    r=rand;        C=cumsum(P);        i=find(r<=C,1,'first');​end

​function z=Sphere(x)​    z=sum(x.^2);​end

完整代码添加QQ1575304183