人工蜂群优化算法

Posted 2021-06-29 博主QQ2449341593

文章目录

• 一、理论基础
• 二、算法流程
• • 1、初始化阶段
  • 2、引领蜂阶段
  • 3、跟随蜂阶段
  • 4、侦察蜂阶段
  • 5、食物源
• 三、MATLAB程序实现
• • 1、清空环境变量
  • 2、问题设定
  • 3、参数设置
  • 4、初始化蜜蜂种群
  • 5、迭代优化
  • 6、结果显示
• 四、参考文献

 

一、理论基础

受到蜜蜂群体的有组织的觅食过程的启发，Karaboga提出了模拟蜜蜂群体觅食过程的人工蜂群(Artificial Bee Colony) 算法用于解决多维度多峰谷的优化问题。该算法创始之初被用来寻找Sphere、Rosenbrock和Rastrigin函数的最小值。
首先对蜜蜂基于摇摆舞进行觅食的过程特征进行介绍。在图1中，存在两个已发现的食物源A和B。初始时，潜在工蜂以非雇佣蜂的身份进行搜索。它并不知道蜂房附近的任何蜜源的信息。因此，它有以下两个可能的选择：
（1）成为一个侦察蜂，秉着自身潜在动力或外在因素自发的搜索蜂房附近的区域(见图1中的S)；
（2）在观看摆尾舞后，成为一个被招募者，并开始搜索蜜源(见图1中的R)。
在定位蜜源之后，该蜜蜂能够利用自身的能力来记住食物源的位置，并立刻对它进行探索。该蜜蜂现在成为了一个雇佣蜂。雇佣蜂采到蜂蜜后，从蜜源处返回蜂房并将蜂蜜卸载到蜜室中。在卸载完蜂蜜后，雇佣蜂有下列三个选择：
（1）放弃已经采集过的蜜源，成为一个受其他摇尾舞招募的跟随者(UF)。
（2）施展摇尾舞技，招募蜂房内的同伴，再次回到原先采集过的食物源(EF1)。
（3）不招募其它的蜜蜂，继续探索采集过的食物源(EF2)。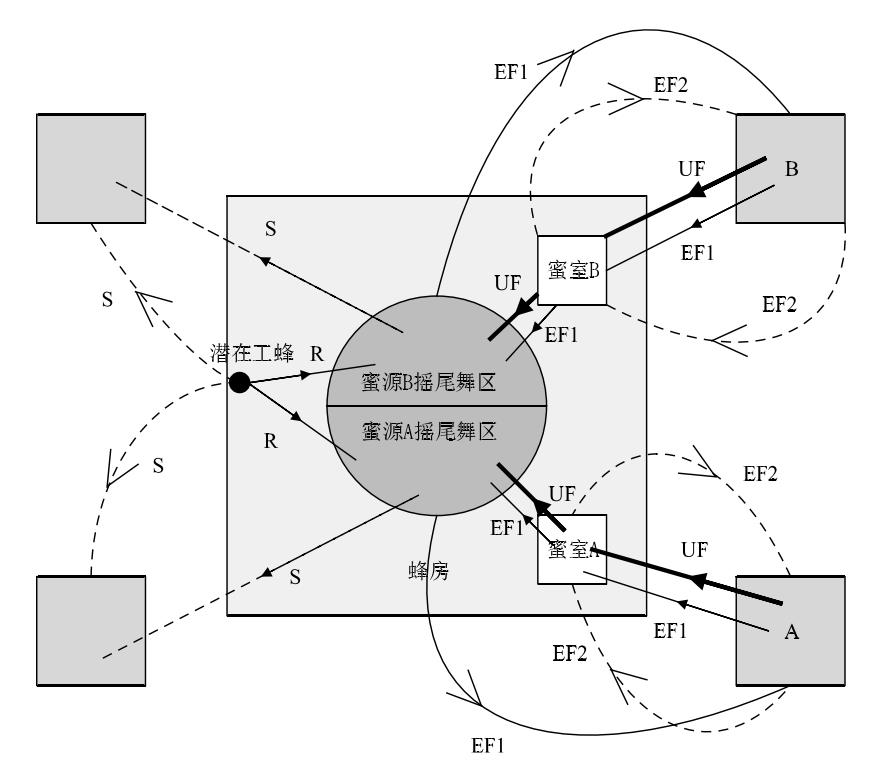

图1 蜜蜂觅食行为图

二、算法流程

人工蜂群算法由连续的四个阶段组成，分别是初始化阶段、引领(雇佣)蜂阶段、跟随蜂阶端和侦察蜂阶段。
人工蜂群算法中将人工蜂群分为引领蜂、跟随蜂和侦察蜂三类，每一次搜索过程中，引领蜂和跟随蜂是先后开采食物源，即寻找最优解，而侦察蜂是观察是否陷入局部最优，若陷入局部最优则随机地搜索其它可能的食物源。每个食物源代表问题一个可能解，食物源的花蜜量对应相应解的质量（适应度值f i t fitfit）。
ABC算法流程图如图2所示。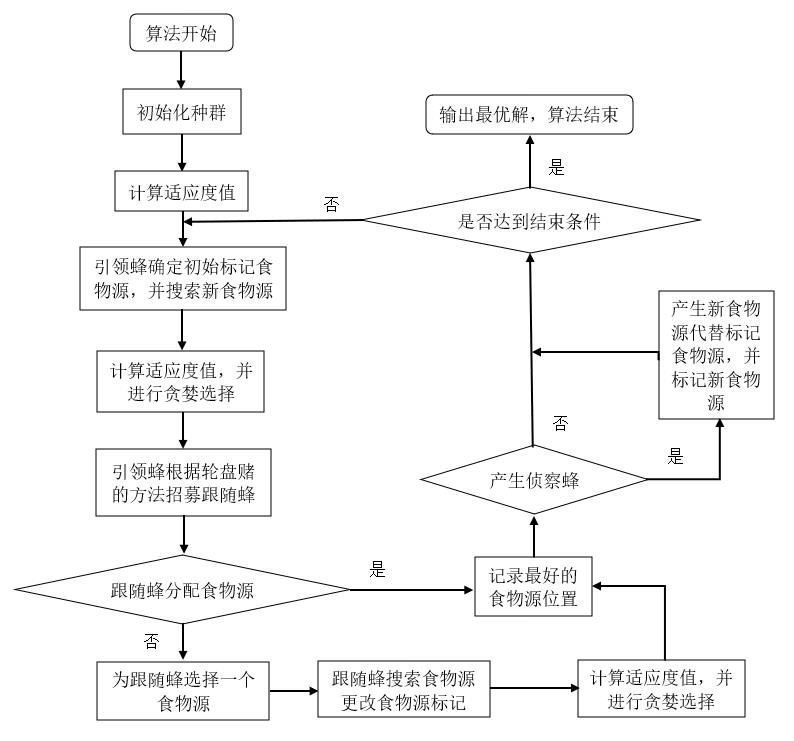

图2 ABC算法流程图

1、初始化阶段

2、引领蜂阶段

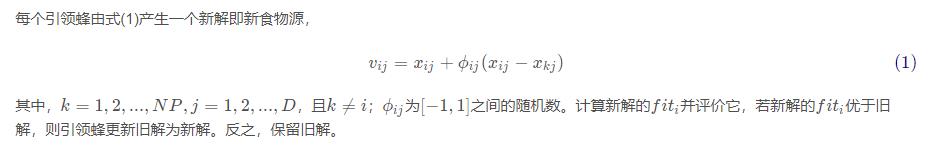3、跟随蜂阶段

4、侦察蜂阶段

5、食物源

 

三、MATLAB程序实现

1、清空环境变量

程序运行之前，清除工作空间Workspace中的变量及Command Window中的命令。具体程序如下：

%% 清空环境变量
clc;
clear;
close all;

2、问题设定

在进行优化之前，需要明确优化的目标函数。具体程序如下：

Rosenbrock函数的三维立体图如图3所示。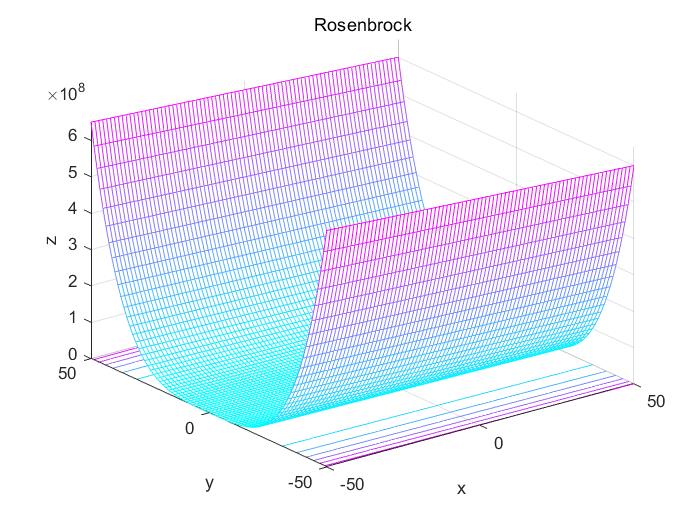

图3 Rosenbrock函数的三维立体图

Rosenbrock函数的代码如下：

function [y] = Rosenbrock(xx)
%% Rosenbrock函数
d = length(xx);
sum = 0;
for ii = 1:(d-1)
	xi = xx(ii);
	xnext = xx(ii+1);
	new = 100*(xnext-xi^2)^2 + (xi-1)^2;
	sum = sum + new;
end
y = sum;

3、参数设置

代码如下：

%% ABC参数
%% ABC参数
MaxIt = 200;                  % 最大迭代次数
nPop = 100;                   % 蜂群大小
nOnlooker = nPop;             % 侦察蜂个数
L = round(0.6*nVar*nPop);     % 探索极值限制参数
a = 1;                        % 加速度系数上限

4、初始化蜜蜂种群

在计算之前，需要对蜜蜂种群进行初始化。同时，为了加快程序的执行速度，对于程序中涉及的一些过程变量，需要预分配其存储容量。具体程序如下：

%% 初始化
% 置空蜜蜂矩阵
empty_bee.Position = [];
empty_bee.Cost = [];
% 初始化蜂群数组
pop = repmat(empty_bee, nPop, 1);
% 初始化最优解
BestSol.Cost = inf;
% 产生初始种群
for i = 1:nPop
    pop(i).Position = unifrnd(VarMin, VarMax, VarSize);
    pop(i).Cost = CostFunction(pop(i).Position);
    if pop(i).Cost <= BestSol.Cost
        BestSol = pop(i);
    end
end
% 丢解计数器
C = zeros(nPop, 1);
% 保存最优函数值的数组
BestCost = zeros(MaxIt, 1);

5、迭代优化

代码如下：

%% ABC迭代
for it = 1:MaxIt
    % 引领蜂
    for i = 1:nPop
        % 随机选择不等于i的k
        K = [1:i-1 i+1:nPop];
        k = K(randi([1 numel(K)]));
        % 定义加速度系数
        phi = a*unifrnd(-1, +1, VarSize);
        % 新的蜜蜂位置
        newbee.Position = pop(i).Position+phi.*(pop(i).Position-pop(k).Position);
        % 边界处理
        newbee.Position = max(newbee.Position, VarMin);
        newbee.Position = min(newbee.Position, VarMax);
        % 新的蜜蜂函数值
        newbee.Cost = CostFunction(newbee.Position);
        % 比较
        if newbee.Cost <= pop(i).Cost
            pop(i) = newbee;
        else
            C(i) = C(i)+1;
        end
    end
    % 计算适应度值和选择概率
    F = zeros(nPop, 1);
    MeanCost = mean([pop.Cost]);
    for i = 1:nPop
        % 将函数值转换为适应度
        if pop(i).Cost >= 0
            F(i) = 1/(1+pop(i).Cost);
        else
            F(i) = 1+abs(pop(i).Cost);
        end
    end
    P = F/sum(F);
    % 跟随蜂
    for m = 1:nOnlooker
        % 选择食物源
        i = RouletteWheelSelection(P);
        % 随机选择不等于i的k
        K = [1:i-1 i+1:nPop];
        k = K(randi([1 numel(K)]));
        % 定义加速度系数
        phi = a*unifrnd(-1, +1, VarSize);
        % 新的蜜蜂位置
        newbee.Position = pop(i).Position+phi.*(pop(i).Position-pop(k).Position);
        % 边界处理
        newbee.Position = max(newbee.Position, VarMin);
        newbee.Position = min(newbee.Position, VarMax);
        % 新的蜜蜂函数值
        newbee.Cost = CostFunction(newbee.Position);
        % 比较
        if newbee.Cost <= pop(i).Cost
            pop(i) = newbee;
        else
            C(i) = C(i) + 1;
        end
    end
    % 侦察蜂
    for i = 1:nPop
        if C(i) >= L    % 超出探索极值参数
            maxPos = max(pop(i).Position);
            minPos = min(pop(i).Position);
            for j = 1:numel(pop(i).Position)
                pop(i).Position(j) = minPos+rand*(maxPos-minPos);
            end
            pop(i).Cost = CostFunction(pop(i).Position);
            C(i) = 0;
        end
    end
    % 更新每轮最优解
    for i = 1:nPop
        if pop(i).Cost <= BestSol.Cost
            BestSol = pop(i);
        end
    end
    % 保存每轮最优解
    BestCost(it) = BestSol.Cost;
    % 显示迭代信息
    disp(['Iteration ' num2str(it) ': Best Cost = ' num2str(BestCost(it))]);
end

6、结果显示

为了更为直观地对结果进行观察和分析，以图形的形式将结果显示出来，具体程序如下：

%% 结果显示
figure;
% plot(BestCost, 'LineWidth', 2);
semilogy(BestCost, 'r', 'LineWidth', 2);
xlabel('Iteration');
ylabel('Best Cost');
grid on;

ABC算法进化过程如图4所示。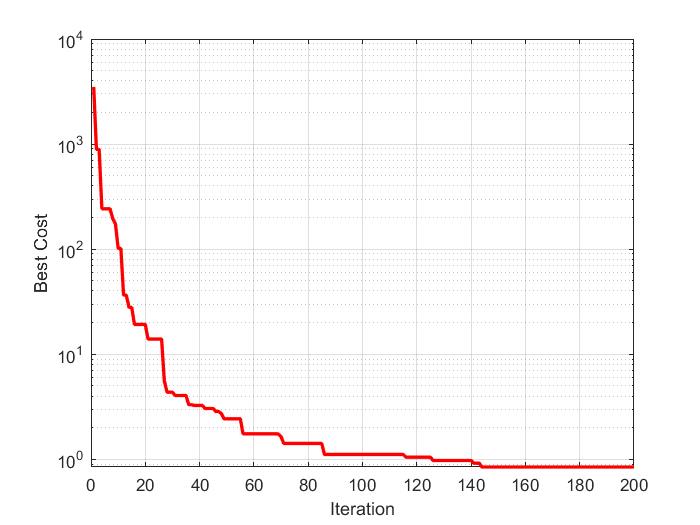

图4 ABC算法进化过程

代码下载https://www.cnblogs.com/matlabxiao/p/14883637.html

四、参考文献

[1] Karaboga D . An idea based on honey bee swarm for numerical optimization[J]. 2005.
[2] 于文杰. 基于人工蜂群算法的无线传感器网络部署问题研究[D].