智能优化算法：人工蜂群算法

Posted 2023-04-06

参考技术A @[toc]
摘要：人工蜂群算法(artificial bee colony，ABC)是由土耳其学者Karaboga 于 2005 年提出，它是模拟蜜蜂的采蜜行为来解决生活中一些多维和多模的优化问题，它最初应用于数值优化问题，自提出以来受到了众多学者极大的关注，并广泛应用到神经网络、数据挖掘、工程应用、图像识别等多个领域。

在 ABC 算法里，用蜜源的位置来表示解，用蜜源的花粉数量表示解的适应值。所有的蜜蜂划分为雇佣蜂、跟随蜂、探索蜂三组。雇佣蜂和跟随蜂各占蜂群总数的一半。雇佣蜂负责最初的寻找蜜源并采蜜分享信息，跟随蜂负责呆在蜂巢里根据雇佣蜂提供的信息去采蜜，探索蜂在原有蜜源被抛弃后负责随机寻找新的蜜源来替换原有的蜜源。与其他群智能算法一样，ABC 算法是迭代的。对蜂群和蜜源的初始化后，反复执行三个过程，即雇佣蜂、跟随蜂、探索蜂阶段，来寻找问题的最优解。每个阶段描述如下:

对 ABC 算法的参数进行初始化，这些参数有蜜源数 、蜜源确定被抛弃的次数 、迭代终止次数。在标准 ABC 算法里，蜜源的数目 与雇佣蜂数相等，也与跟随蜂数相等。产生某个蜜源的公式为:

其中: 代表第 个蜜源 的第 维度值， 取值于 ， 取值于 ; 和 分别代表第 维的最小值和最大值。初始化蜜源就是对每个蜜源的所有维度通过以上公式赋一个在取值范围内的随机值，从而随机生成 个最初蜜源。

在雇佣蜂阶段，雇佣蜂用以下公式来寻找新蜜源:

其中: 代表邻域蜜源， 取值于 ，且 不等于 ; 是取值在[-1,1]的随机数，通过式(2)得到新蜜源后，利用贪婪算法，比较新旧蜜源适应值，选择优者。

雇佣蜂阶段结束，跟随蜂阶段开始。在该阶段，雇佣蜂在舞蹈区分享蜜源信息。跟随蜂分析这些信息，采用轮盘赌策略来选择蜜源跟踪开采，以保证适应值更高的蜜源开采的概率更大。跟随蜂开采过程与雇佣蜂一样，利用式(2)找寻新蜜源，并留下更优适应者。
蜜源拥有参数 ，当蜜源更新被保留时， 为 0;反之， 加 1。从而 能统计出一个蜜源没有被更新的次数。

如果一个蜜源经过多次开采没被更新，也就是 值过高，超过了预定阈值 ，那么需抛弃这个蜜源，启动探索蜂阶段。这体现了 ABC 里自组织的负反馈和波动属性 。在该阶段里，探索蜂利用式(3)随机寻找新的蜜源来代替被抛弃蜜源。

人工蜂群算法流程

step1.初始化算法参数，生成蜜蜂初始位置

step2.雇佣蜂计算适应度值，比较并保存最优值

step3.跟随蜂选择雇佣蜂更新蜜源位置，计算适应度值，保存最佳值

step4.若有侦察蜂出现，则重新生成初始位置并执行更新选优，否则继续执行step5

step5.若迭代次数小于预设的迭代次数，则转到step2；否则输出最优解

[1]何尧,刘建华,杨荣华.人工蜂群算法研究综述[J].计算机应用研究,2018,35(05):1281-1286.

https://mianbaoduo.com/o/bread/aJWVkps=

https://mianbaoduo.com/o/bread/YZWalJxr

matlab基于人工蜂群算法的函数优化分析matlab优化算法十一

基于人工蜂群算法的函数优化分析

自然界中的群居昆虫，它们虽然个体结构简单，但是通过个体间的合作却能够表现出极其复杂的行为能力。受这些社会性昆虫群体行为的启发，研宄者通过模拟这些群体的行为提出了群集智能算法。这些群集智能算法的岀现，使得一些比较复杂且难于用经典优化算法进行处理的问题得到了有效的解决，同时这些算法已不断地运用于解决实际问题，在很多领域得到了广泛的应用，如调度问题，人工神经网络，组合优化问题等工程领域。人工蜂群算法（ABC）是一种模拟蜜蜂采蜜行为的群集智能优化算法，它为解决存在于科学领域的全局优化问题提供了一种新的方法。由于它具有控制参数少、易于实现、计算简单等优点，已经被越来越多的研究者所关注。

人工蜂群算法概述

人工蜂群算法（ABC）作为一种模拟蜜蜂蜂群智能搜索行为的生物智能优化算法，2008年引入国内，是一种新型的全局寻优算法，能够解决计算机科学、管理科学、控制工程等领域的几乎全部全局优化问题。又由于人工蜂群算法（ABC）控制参数少、易于实现、计算简洁，从而成为学术界研究的焦点。ABC算法已经成功地应用到各个领域，如图像处理、调度问题、旅行商问题、人工神经网络训练、动态路径选择、蛋白高级结构预测、无线传感器网络等；此外，ABC算法还与其它方法相互结合，比如将粒子群算法、分布式思想、局部搜索算子和保持种群多样性策略等与ABC算法相结合，以此提高算法的整体优化性能。
ABC算法把优化问题的解看作是具有经验和智慧的智能个体即蜜蜂，将优化问题的目标函数值度量成蜜蜂对环境的适应能力，将定量问题形象化、智能化，为解决大量复杂的实际问题提供了新的思路。ABC算法在各个领域中的成功应用，显示了ABC算法具有强大的生命力，无论从理论研究还是应用研究的角度分析，ABC算法及其应用研究都具有重要的学术意义和现实价值。

算法原理人

工蜂群算法（ABC）是由 Karaboga于2005年提出的一种新颖的群集智能优化算法。人工蜂群算法（ABC）主要模拟蜂群的智能采蜜行为，蜜蜂根据各自的分工进行不同的采蜜活动，并实现蜜源信息的共享和交流，从而找到问题的最优解在人工蜂群算法（ABC）算法中，人工蜂群包含3个组成部分：采蜜蜂、观察蜂和侦察蜂。在蜂群中，岀去寻找蜜源的蜜蜂是采蜜蜂，在舞蹈区内等待选择蜜源的蜜蜂是观察蜂，而在一定情况下进行随机搜索蜜源的蜜蜂是侦察蜂。在蜂群进化过程中，采蜜蜂和观察蜂负责执行开采过程，而侦察蜂执行探索过程。群体的一半由采蜜蜂构成，另一半由观察蜂构成。每一处蜜源仅仅有一个采蜜蜂，也就是采蜜蜂的个数与蜜源的个数相等。


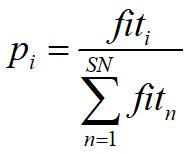
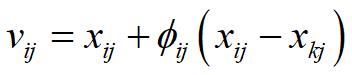
实际上，ABC算法中包含四个选择过程：（1）观察蜂根据一定的选择概率选择蜜源的全局选择过程；（2）采蜜蜂和观察蜂结合自身的局部信息进行邻域搜索产生候选位置的局部选择过程；（3）所有人工蜂对新旧蜜源进行比较，保留较好蜜源的贪婪选择过程；（4）侦察蜂搜索新蜜源的随机选择过程由以上的分析可知，ABC算法作为一种群集智能随机优化算法，能够实现模拟蜂群的高效采蜜行为，而且在全局搜索能力和局部搜索能力之间有一个较好的平衡，从而使得算法的性能得到了很大的提升。

ABC算法流程

基本ABC算法中搜索方程具有很大的随机性，为了加快算法的收敛速度使种群能够朝着较好个体的方向进化，对ABC算法搜索方程的改进是很有必要的。并且改进算法的实现步骤只是把原来的搜索方程替换为改进的搜索方程，其余都不改变。

人工蜂群算法函数优化与 MATLAB实现

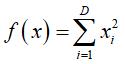
% 人工蜂群算法
% 参数说明：
% Foods [FoodNumber][D]; % 初始化的食物源
% ObjVal[FoodNumber];    % 目标函数
% Fitness[FoodNumber];   % 适应度值，目标函数值的倒数
% trial[FoodNumber];     % 拖尾参数
% prob[FoodNumber];      % 计算的概率值
% solution [D];          % 产生的新解，候选位置 produced by v_{ij}=x_{ij}+\\phi_{ij}*(x_{kj}-x_{ij}) j is a randomly chosen parameter and k is a randomlu chosen solution different from i*/
% ObjValSol;             % 新解下的目标函数值
% FitnessSol;            % 新解的适应度值
% neighbour, param2change; 对应于方程 v_{ij}=x_{ij}+\\phi_{ij}*(x_{kj}-x_{ij})*/
% GlobalMin;             % 目标函数值最小值
% GlobalParams[D];       % 每一次运行该算法得到的最优个体值，未知数的解
% GlobalMins[runtime];   % 循环计算该算法的次数，记录下的最小解，验证算法的鲁棒性和稳定性
clc,clear,close all
warning off
feature jit off
tic
% 算法参数
NP=20;           % 蜂群大小
FoodNumber=NP/2; % 蜂群食物源数量，也就是产生 解 的个数
limit=10;       % 经过“limit”次采蜜蜂和观察蜂的循环搜索之后，不能够被改进，那么该位置将被放弃
maxCycle=500;    % 最大迭代循环

%/* Problem specific variables*/
objfun='Sphere';     % 待优化函数
D=10;               % 未知数为100个
ub=ones(1,D)*10;    % 未知量取值下边界
lb=ones(1,D)*(-10); % 未知量取值上边界
runtime=1;           % 算法运行次数，一般设置1即可

GlobalMins=zeros(1,runtime);   % 适应度最小值初始化

for r=1:runtime
  
% 初始化变量值
Range = repmat((ub-lb),[FoodNumber 1]);       % 最大值
Lower = repmat(lb, [FoodNumber 1]);           % 最小值
Foods = rand(FoodNumber,D) .* Range + Lower;  % 初始化个体

ObjVal=feval(objfun,Foods);       % 目标函数值
Fitness=calculateFitness(ObjVal); % 适应度值，取其导数，为最小值

% 设定拖尾矩阵，初始化
trial=zeros(1,FoodNumber);

% 找到最好的食物源
BestInd=find(ObjVal==min(ObjVal));
BestInd=BestInd(end);
GlobalMin=ObjVal(BestInd);     % 函数值最小
GlobalParams=Foods(BestInd,:); % 相应的食物源个体

iter=1;
while ((iter <= maxCycle)),  % 迭代开始

% 采蜜蜂
    for i=1:(FoodNumber)
        % 参数随机可变
        Param2Change=fix(rand*D)+1;
        % 随机选择相连个体
        neighbour=fix(rand*(FoodNumber))+1;
        % 随机选择的个体不等于i
        while(neighbour==i)
            neighbour=fix(rand*(FoodNumber))+1;
        end;
        
       sol=Foods(i,:);  % 个体选择
       %  /*v_{ij}=x_{ij}+\\phi_{ij}*(x_{kj}-x_{ij}) */
       sol(Param2Change)=Foods(i,Param2Change)+(Foods(i,Param2Change)-Foods(neighbour,Param2Change))*(rand-0.5)*2;
        
       % 个体取值范围约束
        ind=find(sol<lb); % 最小值约束
        sol(ind)=lb(ind);
        ind=find(sol>ub); % 最大值约束
        sol(ind)=ub(ind);
        
        % 估计新的目标函数值和适应度值
        ObjValSol=feval(objfun,sol);
        FitnessSol=calculateFitness(ObjValSol);
        
       % 更新最优个体值
       if (FitnessSol>Fitness(i)) % 如果新产生的个体值适应度值越大，则表明函数值越小，则个体最优
            Foods(i,:)=sol;
            Fitness(i)=FitnessSol;
            ObjVal(i)=ObjValSol;
            trial(i)=0;
        else
            trial(i)=trial(i)+1; % /*if the solution i can not be improved, increase its trial counter*/
       end;
    end;
    
% 观察蜂
% 计算概率
% 观察蜂根据与蜜源相关的概率值选择蜜源，概率值计算公式
% prob(i)=a*fitness(i)/max(fitness)+b*/
prob=(0.9.*Fitness./max(Fitness))+0.1;  
i=1;
t=0;
while(t<FoodNumber)
    if(rand<prob(i))
        t=t+1;
        % 继续随机选择个体
        Param2Change=fix(rand*D)+1;
        % 随机选择相连个体
        neighbour=fix(rand*(FoodNumber))+1;
        % 随机选择的个体不等于i      
        while(neighbour==i)
            neighbour=fix(rand*(FoodNumber))+1;
        end;
       sol=Foods(i,:);  % 个体选择
       %  /*v_{ij}=x_{ij}+\\phi_{ij}*(x_{kj}-x_{ij}) */
       sol(Param2Change)=Foods(i,Param2Change)+(Foods(i,Param2Change)-Foods(neighbour,Param2Change))*(rand-0.5)*2;
        
       % 个体取值范围约束
       ind=find(sol<lb); % 最小值约束
       sol(ind)=lb(ind);
       ind=find(sol>ub); % 最大值约束
       sol(ind)=ub(ind);
        
       % 估计新的目标函数值和适应度值
       ObjValSol=feval(objfun,sol);
       FitnessSol=calculateFitness(ObjValSol);
        
       % 更新最优个体值
       if (FitnessSol>Fitness(i)) % 如果新产生的个体值适应度值越大，则表明函数值越小，则个体最优
            Foods(i,:)=sol;
            Fitness(i)=FitnessSol;
            ObjVal(i)=ObjValSol;
            trial(i)=0;
        else
            trial(i)=trial(i)+1; % /*if the solution i can not be improved, increase its trial counter*/
       end;
    end;
    
    i=i+1;
    if (i==(FoodNumber)+1) 
        i=1;
    end;   
end; 

    % 记录最好的目标函数值
    ind=find(ObjVal==min(ObjVal));
    ind=ind(end);
    if (ObjVal(ind)<GlobalMin)
        GlobalMin=ObjVal(ind);      % 最优目标函数值
        GlobalParams=Foods(ind,:);  % 最优个体
    end;
         
         
% 侦察蜂
% 如果某一次循环拖尾次数大于设定limit，则重新更新个体，重新计算
ind=find(trial==max(trial));
ind=ind(end);
if (trial(ind)>limit)
    Bas(ind)=0;
    sol=(ub-lb).*rand(1,D)+lb;
    ObjValSol=feval(objfun,sol);
    FitnessSol=calculateFitness(ObjValSol);
    Foods(ind,:)=sol;
    Fitness(ind)=FitnessSol;
    ObjVal(ind)=ObjValSol;
end;

fprintf('iter=%d ObjVal=%g\\n',iter,GlobalMin);
iter=iter+1;

end % End of ABC

GlobalMins(r)=GlobalMin;
end; % end of runs
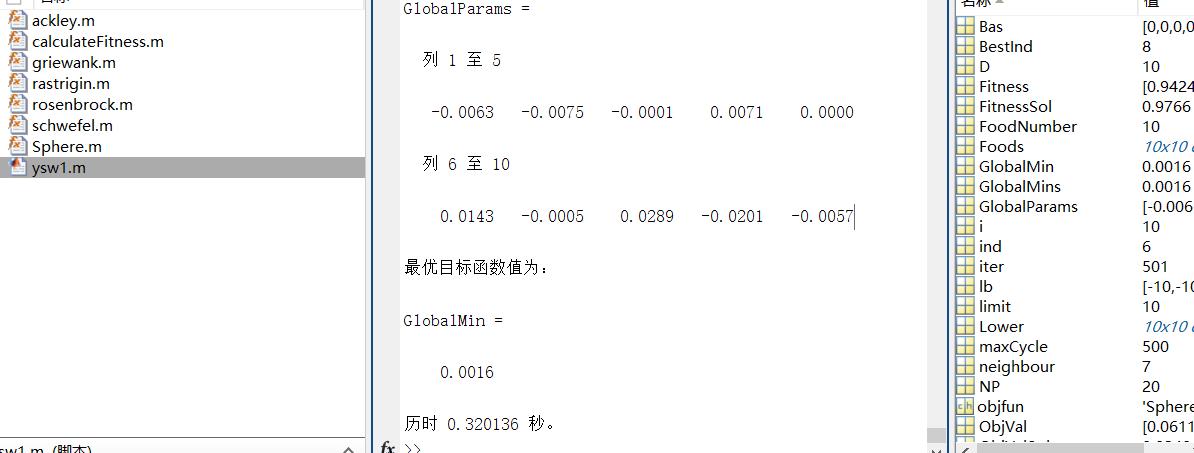
disp('最优解为：')
GlobalParams
disp('最优目标函数值为：')
GlobalMin

toc
% save all

人工蜂群算法ABC探讨

在进化算法中，广大学者们对其进化搜索方程的研究有很多，并且通过算法改进使算法的性能有了一定的提升。比如，在粒子群算法（PSO）中，学者们主要针对粒子群优化算法的早熟问题，在粒子的平均位置或全局最优位置上加入髙斯扰动以阻止粒子陷入局部最优，还有学者通过分析粒子群算法更新方程的缺陷，加入用于避免陷入局部最优的扰动项（加入惯性杈重等）对其进行改进，使得改进算法在优化性能上有了较大的提高；同样，在差分进化算法（DE）中，有学者对其差分变异方程进行改进，以进一步提升算法的整体性能，如有学者在差分进化算法（DE）中引入三角法变异，将个体看作超三角形的中心点并且沿着超三角形的三条边分别以不同的步长移动来产生新的变异个体，从而帮助算法跳出局部最优；有学者利用质心变异操作对差分进化算法的变异方程进行改进等等由于人工蜂群算法（ABC）算法的搜索方程与PSO算法的进化方程、DE算法的差分变异方程很相似，因此受研究者对PSO算法进化方程和DE算法变异方程改进的启发，一些学者也对ABC算法中的搜索方程进行改进以提升算法的性能，如有学者提出了基于改进搜索方程的ABC算法，利用全局最优解的信息指导候选解的搜索从而提高了ABC算法的开采能力；有学者在ABC算法的搜索方程中引入上一代个体的信息以及引入灵敏度对观察蜂的选择机制进行改进；也有学者分别在采蜜蜂、观察蜂和侦察蜂阶段的搜索方程中引进全局最优解的信息以加快收敛速度。
ABC算法的搜索方程具有较好的全局搜索能力，但其局部搜索能力体现较弱。而在基于种群的进化算法中，全局搜索和局部搜索之间达到有效的平衡才能使算法的性能得到很好的提升。

代码下载地址https://download.csdn.net/download/weixin_46567845/19814308