从基变换的角度理解旋转矩阵R
Posted 李迎松~
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了从基变换的角度理解旋转矩阵R相关的知识,希望对你有一定的参考价值。
在理解相机坐标系时,我们一定会接触相机的外参矩阵R,它将世界坐标系下的坐标转换到相机坐标系下:
P
c
=
R
∗
P
w
+
t
P_c=R*P_w+t
Pc=R∗Pw+t
这实际上是两个坐标系之间的变换,我们知道
R
R
R矩阵是一个正交矩阵,所以它的3个行(列)向量是3维向量空间的一组标准正交基,而一组标准正交基可以作为一个坐标系的三个基向量。那么我们的
R
R
R矩阵如何和两个坐标系的基向量联系起来呢?
我们先画出两个坐标系
X
w
Y
w
Z
w
X_wY_wZ_w
XwYwZw和
X
c
Y
c
Z
c
X_cY_cZ_c
XcYcZc:
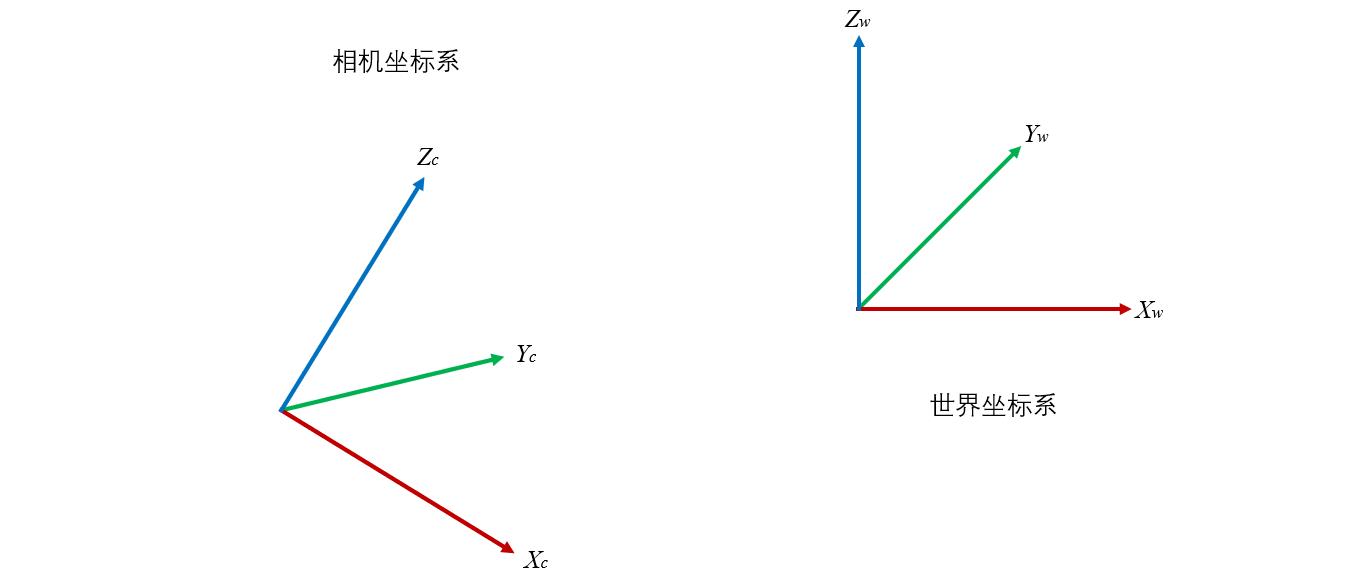
我们要讨论的是如何把某一点
P
P
P 在世界坐标系上的坐标转换成相机坐标系上的坐标。
暂且不考虑两个坐标系之间的平移,于是将相机坐标系的原点移动到世界坐标系的原点,像这样:
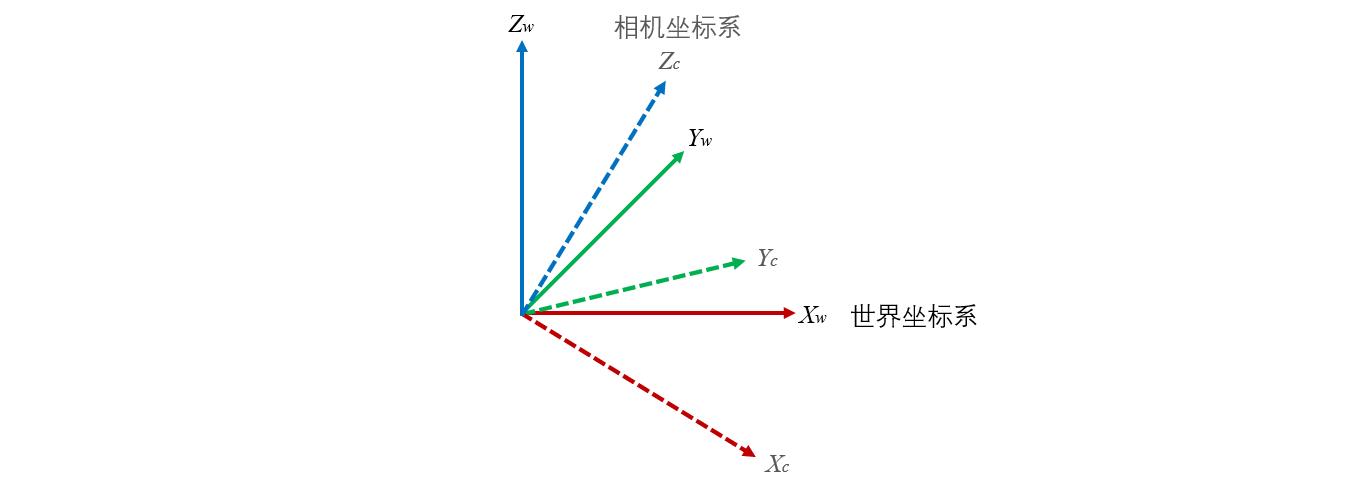
我们可以标出两个坐标系的基向量组
e
w
(
e
⃗
w
x
,
e
⃗
w
y
,
e
⃗
w
z
)
e_w(\\vece_wx,\\vece_wy,\\vece_wz)
ew(ewx,ewy,ewz)和
e
c
(
e
⃗
c
x
,
e
⃗
c
y
,
e
⃗
c
z
)
e_c(\\vece_cx,\\vece_cy,\\vece_cz)
ec(ecx,ecy,ecz)。它们都在世界坐标系下。
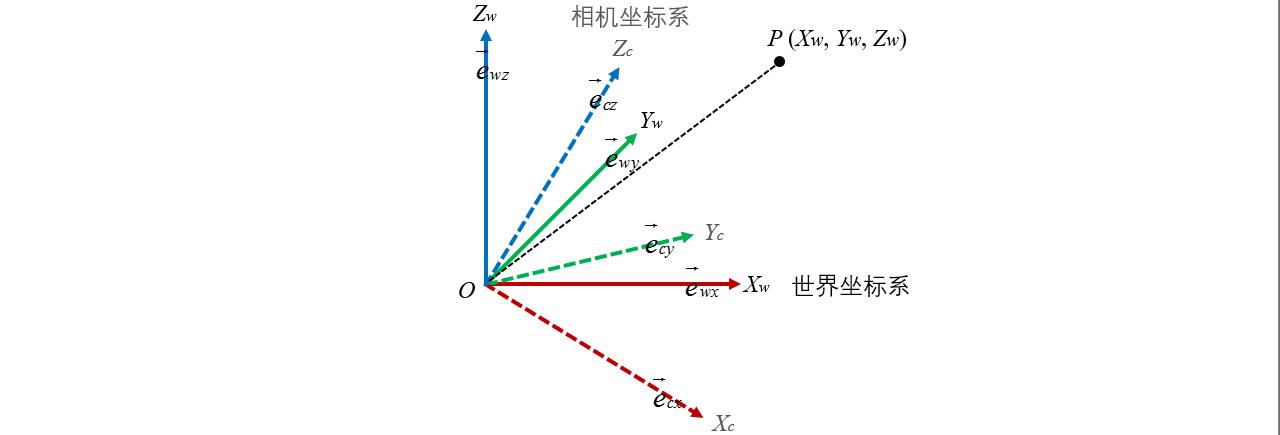
接下来,再讨论如何把世界坐标系上的一点
P
(
X
w
,
Y
w
,
Z
w
)
P(X_w,Y_w,Z_w)
P(Xw,Yw,Zw)转换到相机坐标系下
P
(
X
w
,
Y
w
,
Z
w
)
→
P
(
X
c
,
Y
w
,
Z
w
)
P(X_w,Y_w,Z_w)→P(X_c,Y_w,Z_w)
P(Xw,Yw,Zw)→P(Xc,Yw,Zw)
在世界坐标系下,基向量组
e
w
(
e
⃗
w
x
,
e
⃗
w
y
,
e
⃗
w
z
)
e_w(\\vece_wx,\\vece_wy,\\vece_wz)
ew(ewx,ewy,ewz)为单位阵,也就是
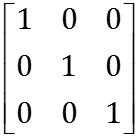
其中 e ⃗ w x = ( 1 , 0 , 0 ) T \\vece_wx=(1,0,0)^T ewx=(1,0,0)T, e ⃗ w y = ( 0 , 1 , 0 ) T \\vece_wy=(0,1,0)^T ewy=(0,1,0)T, e ⃗ w z = ( 0 , 0 , 1 ) T \\vece_wz=(0,0,1)^T ewz=(0,0,1)T。
我们知道 P P P在世界坐标系下的坐标实际上是以上三组基向量的线性组合,即 P w = X w ∗ e ⃗ w x + Y w ∗ e ⃗ w x + Z w ∗ e ⃗ w x P_w=X_w*\\vece_wx+Y_w*\\vece_wx+Z_w*\\vece_wx Pw=Xw∗ewx+Yw∗ewx+Zw∗ewx
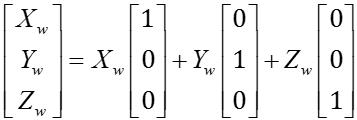
这便是坐标的基向量表示法了。
那么我们把
P
P
P点的坐标变换到基向量组
e
c
(
e
⃗
c
x
,
e
⃗
c
y
,
e
⃗
c
z
)
e_c(\\vece_cx,\\vece_cy,\\vece_cz)