二叉树DP解题套路
Posted 东条希尔薇
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了二叉树DP解题套路相关的知识,希望对你有一定的参考价值。
算法笔记源代码和博客备份都在这:https://gitee.com/dongtiao-xiewei/algorithm/tree/master
我们先通过一道简单的题来引出我们今天的套路
判断是否为平衡二叉树
平衡二叉树的定义,每个结点的高度差都>=1
大家可以先看看我以前常规的解法,对每个遍历到的结点求高度,再求某个结点的左右子树的高度,再判断左右子树分别是不是平衡二叉树
int maxDepth(struct TreeNode* root)//求高度的函数
if(!root)
return 0;
int left=maxDepth(root->left);
int right=maxDepth(root->right);
return left>right ? left+1 :right+1;
bool isBalanced(struct TreeNode* root)
if(!root)
return true;
int left=maxDepth(root->left);//分别递归左右结点的高度
int right=maxDepth(root->right);
return abs(left-right)<2//判断当前结点,和左右子树
&&isBalanced(root->left)
&&isBalanced(root->right);
当然这道题,我们还可以这样思考:
我们可以取任意一个结点x,来思考它本身和它左右子树的性质来解决问题
1.首先,是平衡二叉树有哪些可能性?
当然不满足二叉树的特性就不是平衡二叉树了,我们来列出,有哪些情况发生,会让这颗树不是平衡二叉树?
- 左右子树任意一个不是平衡二叉树
- x的左右子树高度差大于1
我们需要了解这些信息,就需要从左右子树之中获取,那么,怎么获取这些数据呢?我们又需要哪些数据来求解呢?
2.列出我们所需要的信息
我们当然需要左右树是否为平衡二叉树和左右子树分别的高度这些信息,来证明我们的可能性是否成立,我们可以把它列为一个结构体
class Info
public:
bool isBT;//是否为平衡二叉树
int height;//树的高度
3.递归求解,逐渐从左右树中获取信息,并且加工我们想要的信息
首先处理特殊情况,当x为空树时,我们可以把它理解成是平衡二叉树和高度为0的树,所以就返回(1,0)
我们首先从左右树获取我们想要的信息
Info leftInfo=_isBalanced(root->left);
Info rightInfo=_isBalanced(root->right);
获取了信息后,我们可以把当前以x为根的树得到的信息结合起来,按照我们列出的可能性,做统一处理
- 首先,如果左树,右树有一个不是平衡二叉树,那么以x为根的树就不是平衡二叉树
- 然后,再判断以x为根的树,如果x左右子树高度之差大于1,也不是平衡二叉树
- 得到这些信息后,做统一返回
ans.isBST=1;//首先默认是平衡二叉树,只要遇到了false的情况才改变值,不然都为1
ans.height=max(leftInfo.height,rightInfo.height)+1;//高度的求法,这里不做详细阐述
if(!leftInfo.isBST||!rightInfo.isBST)
ans.isBST=0;//第一种情况的判断
if(abs(leftInfo.height-rightInfo.height)>1)
ans.isBST=0;//第二种情况的判断
套路直通车
那么,通过这道题,我们可以总结出我们套路解题的步骤:
- 以树上任意点x为头,分析答案有哪些可能性,一一列举
- 列举出验证我们提出的可能性需要哪些信息,一一列举,将其归为一个info类
- 从左右树获取信息,以x为根结点,统一加工这些信息,一一判断可能性是否成立
总结:这种套路本质是对二叉树的后序遍历,先处理左右子树的信息后统一拿给x进行处理。时间复杂度为O(n),(遍历整棵树)
接下来我们再列举几道题,加深大家对这种套路的理解
判断搜索二叉树
搜索二叉树的定义:节点的左子树只包含小于当前节点的数。
节点的右子树只包含大于当前节点的数。
所有左子树和右子树自身必须也是二叉搜索树。
第一步,我们想想有哪些可能性?
- 结果与x无关,这种可能性下,左右树其中有一个不是完全二叉树
- 结果与x有关,这种可能性下,左右树已经是完全二叉树了,就判断x的值是否满足要求了
第二步,我们需要哪些信息?
通过可能性的列举,我们需要的信息有:
- 左右树是否为BST?(验证与x是否有关)
- 左右树的最大最小值?(验证x是否满足要求)
class Info
public:
bool isBST;
int max;
int right;
Info(bool is=1,int ma=INT_MIN,int mi=INT_MAX)
:isBST(is),max(ma),min(mi)
第三步,加工得到的信息
首先处理最大最小值,这个其实非常简单,先默认最大最小为x结点的值,再分别与我们拿到的左右树最大最小值进行比对就行了
然后处理是不是BST,这个分以下几种情况
- 左右树右一个不是BST,那么这个结点也不是BST
- x不满足要求
当然,这道题空结点我们不好处理,所以直接在条件判断中加入是否为空结点的判断就行了,代码虽然长,但逻辑很简单
class Info
public:
bool isBST;
int max;
int min;
Info(bool is=1,int ma=INT_MIN,int mi=INT_MAX)
:isBST(is),max(ma),min(mi)
;
class Solution
public:
bool isValidBST(TreeNode* root)
return _isValidBST(root).isBST;
Info _isValidBST(TreeNode* root)
Info ans;
Info leftInfo;
Info rightInfo;
if(root->left)
leftInfo=_isValidBST(root->left);
if(root->right)
rightInfo=_isValidBST(root->right);
int _max=root->val;
int _min=root->val;
if(root->left)
_max=max(leftInfo.max,_max);
if(root->right)
_max=max(rightInfo.max,_max);
if(root->left)
_min=min(leftInfo.min,_min);
if(root->right)
_min=min(rightInfo.min,_min);
//以上是最大最小的更新
//以下是BST的判断
if(root->left&&!leftInfo.isBST)
ans.isBST=0;
if(root->right&&!rightInfo.isBST)
ans.isBST=0;
if(root->left&&leftInfo.max>=root->val)
ans.isBST=0;
if(root->right&&rightInfo.min<=root->val)
ans.isBST=0;
ans.max=_max;
ans.min=_min;
return ans;
;
返回任意给定二叉树两结点的最大距离
我们在这里首先明确几点:
绝大部分情况,两个结点之间的高度,就是最大距离
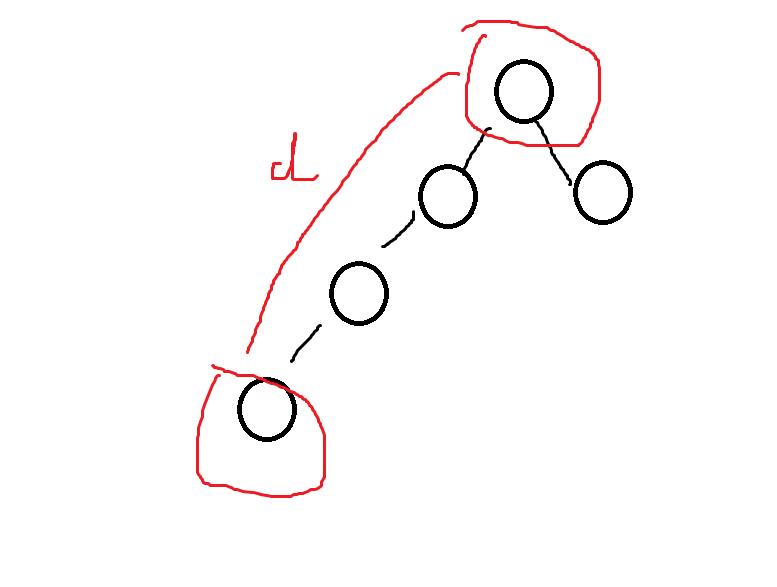
但是也有例外,最大距离可能出在左右子树中
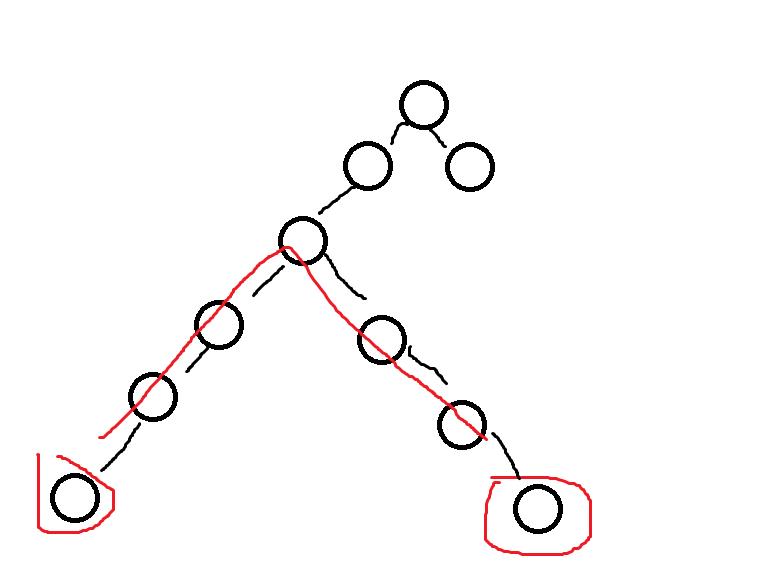
所以我们列举出了几种可能性:
- 结果与x无关,就为左右子树中较大的那一个距离
- 结果与x有关,答案就为左最大高度+右最大高度+1(结点本身)
由于我们不确定是哪一种可能性,所以我们最后答案将这几种结果取最大值
我们就需要以下信息:
树的高度,以及它们的最大距离
class Info
public:
int maxDistance;
int height;
Info(int m, int h)
maxDistance = m;
height = h;
同样加工数据,得出答案
int _maxDistance
info ans;
if (!head)
ans.depth = ans.distance = 0;//空结点结果为0
return ans;
ans.depth = maxDepth(head);//复用求最大深度的函数
info left = _greatestDistance(head->left);
info right = _greatestDistance(head->right);
int p1 = left.distance;
int p2 = right.distance;
int p3 = left.depth + right.depth + 1;
ans.distance = max(p1, p2, p3);//结果求最大值
return ans;
找出树中拥有最多结点的搜索二叉树
我们同样先列举可能性:
- 根结点满足搜索二叉树的性质,那么拥有最大结点树的二叉树就是x本身
- 根结点不满足搜索二叉树的性质, 那么最大结点的树在左右子树的任意一个
我们需要的信息有哪些?
- 我们需要整棵树的大小,来应对整棵树是搜索二叉树的情况
- 需要左右子树中最大搜索二叉树的结点个数,方便最后的返回
- 左右树的最大最小值,判断根结点是否满足性质
至于左右树是否为搜索二叉树的判断,我们仅需要判断左右树最大搜索二叉树结点数是否与结点总数相等就行了,就能节省一个bool变量
所以我们的信息类为
class Info
public:
int allSize;
int maxBSTSize;
int max;
int min;
//构造函数略去
怎么处理信息?
最大最小值的判断在上面已经讲过,这里不再阐述
只不过,我们在判断最大最小值的时候,需要拿到左右子树的信息,我们可以顺便把树的结点在这个环节一并加上
我们能轻松拿到左右结点最大BST的个数,当然结点需要满足以下条件:
左右同为BST,并且满足搜索二叉树的定义
代码如下:
class subBST
public:
int MaxSubBSTSize(BinTreeNode* head)
if (!head)
return 0;
info ans = _MaxSubBSTSize(head);
return ans.BSTSize;
private:
class info
public:
int BSTSize;
int max;
int min;
int allSize;
info(int b = 0,int ma = INT_MIN,int mi = INT_MAX,int all = 0)
:BSTSize(b),max(ma),min(mi),allSize(all)
;
info _MaxSubBSTSize(BinTreeNode* head)
info ans;
if (!head)
return ans;
info left = _MaxSubBSTSize(head->left);
info right = _MaxSubBSTSize(head->right);
int ma = INT_MIN;
int mi = INT_MAX;
ans.allSize = 1;
if (head->left)
ma = max(left.max, ma);
mi = min(left.min, mi);
ans.allSize += left.allSize;
if (head->right)
ma = max(right.max,ma);
mi = max(right.min, mi);
ans.allSize += right.allSize;
ans.max = ma;
ans.min = mi;
int p1 = -1;
if (head->left)
p1 = left.BSTSize;
int p2 = -1;
if (head->right)
p2 = right.BSTSize;
int p3 = -1;
if (left.allSize==left.BSTSize && right.allSize==right.BSTSize)
if (head->data<left.max && head->data>right.min)
p3 = left.allSize + right.allSize + 1;
ans.BSTSize = max(p1, p2, p3);
return ans;
;
判断完全二叉树
列举可能性:
- 左的结点没有超过中点
- 左右为满二叉树
- 左的结点超过了中点
画图求解:(图从左到右分别对应123情况)
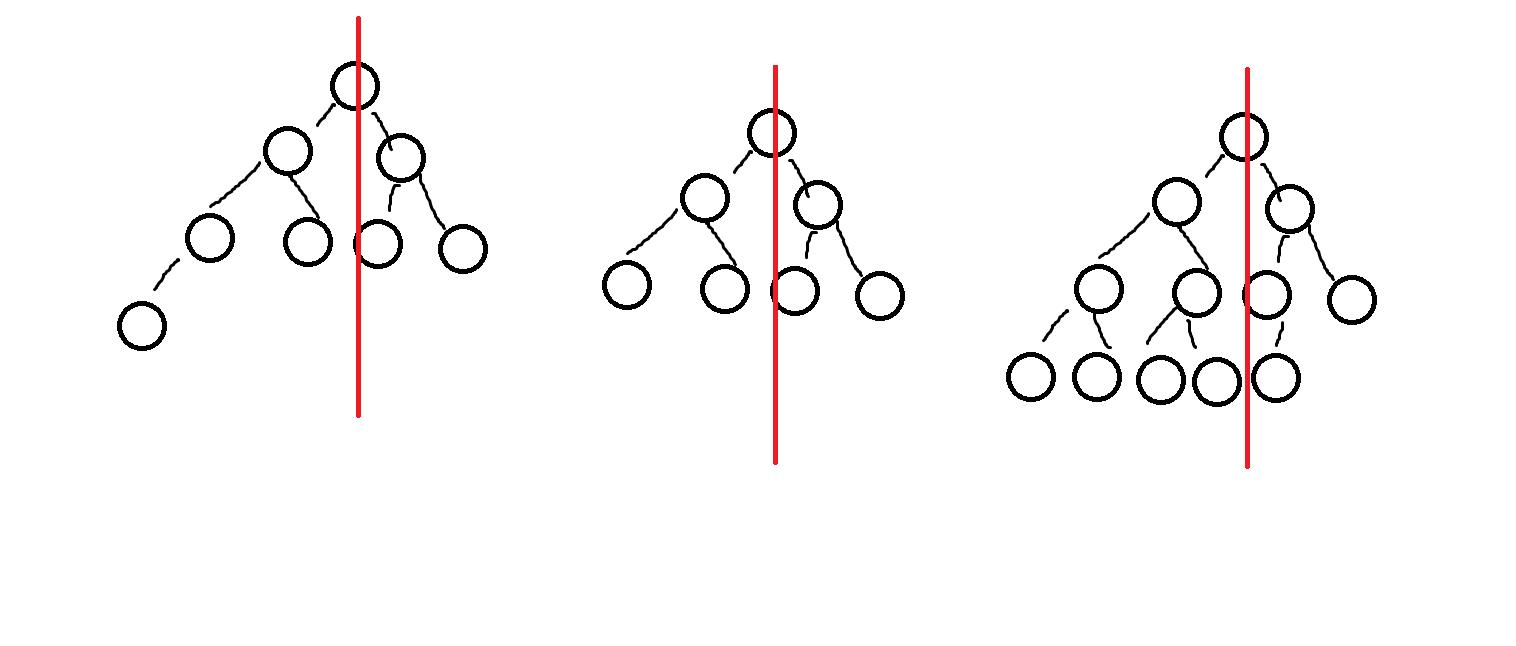
我们就能列举出我们需要的信息了:
左右都为满二叉树
左没有超过中点,也就是左为完全二叉树,右为满二叉树,但右树高度+1=左树高度
左超过中点,也就是左为完全二叉树,右为完全二叉树,但右树高度+1=左树高度
所以我们需要以下信息
- 树的高度
- 是否为CBT
- 是否为满二叉树
class Info
public:
bool isFull;
bool isCBT;
int height;
Info(bool f=1,bool c=1,int h=0)
:isFull(f),isCBT(c),height(h)
;
怎么处理信息?
高度上文有介绍方法,这里不再详细阐述
满二叉树的判断:左右都为满二叉树,且左高度=右高度
是否为完全二叉树,初始值我们设为0,通过我们上面列的可能性分别求解
class CBT
public:
bool isCBT(BinTreeNode* head)
return _isCBT(head).isCBT;
private:
class Info
public:
bool isFull;
bool isCBT;
int height;
Info(bool f=1,bool c=1,int h=0)
:isFull(f),isCBT(c),height(h)
;
Info _isCBT(BinTreeNode* head)
Info ans;
if (!head)
ans.isFull = 1;
ans.isCBT = 1;
ans.height = 0;
return ans;
Info leftInfo = _isCBT(head->left);
Info rightInfo = _isCBT(head->right);
ans.height = leftInfo.height + rightInfo.height + 1;
ans.isFull = leftInfo.isFull && rightInfo.isFull && leftInfo.height == rightInfo.height;
ans.isCBT = 0;
if (leftInfo.isFull && rightInfo.isFull)
ans.isCBT = 1;
if (leftInfo.isCBT && rightInfo.isFull && rightInfo.height + 1 == leftInfo.height)
ans.isCBT = 1;
if (leftInfo.isFull && rightInfo.isFull && rightInfo.height + 1 == leftInfo.height)
ans.isCBT = 1;
if (leftInfo.isFull && rightInfo.isCBT)
ans.isCBT = 1;
return ans;
;
返回二叉树两结点最低公共祖先
我们的可能性如下:
- 汇聚点与x有关:在左右子树中发现了a,b,或者x本身就为a,b,中的一个
- 汇聚点与x无关:已经找到了汇聚点,或者根本没有把a,b找齐
所以,我们的信息如下:
- 发没发现a?
- 发没发现b?
- 发没发现汇聚点?
怎么处理?
如果我们发现了汇聚点,就一路进行返回
如果我们左右子树发现了a,或者x本身为a,就返回true,b同理
最后,如果a和b都找到了,同时答案结点为空,就返回此时的head
代码:
class Ancestor
public:
BinTreeNode* lowestAncestor(BinTreeNode* head, BinTreeNode* a, BinTreeNode* b)
return _lowestAncestor(head, a, b).node;
private:
class Info
public:
bool findA;
bool findB;
BinTreeNode* node;
Info(bool a=0,bool b=0,BinTreeNode* n=nullptr)
:findA(a),findB(b),node(n)
;
Info _lowestAncestor(BinTreeNode* head, BinTreeNode* a, BinTreeNode* b)
Info ans;
if (!head)
ans.findA = 0;
ans.findB = 0;
ans.node = nullptr;
return ans;
Info leftInfo = _lowestAncestor(head->left, a, b);
Info rightInfo = _lowestAncestor(head->right, a, b);
bool findA = 0;
bool findB = 0;
BinTreeNode* node = nullptr;
if (head == a || leftInfo.findA == 1 || rightInfo.findA == 1)
ans.findA = 1;
if (head == b || leftInfo.findB == 1 || rightInfo.findB == 1)
ans.findB = 1;
if (leftInfo.node)
ans.node = leftInfo.node;
else if (rightInfo.node)
ans.node = rightInfo.node;
else
if (findA && findB)
ans.node = head;
return ans;
;
树形DP应用题:最大快乐值
题意:假设公司的上下级为一颗多叉树关系,你是公司的董事长,现在要请你公司成员参数宴席,每个员工都有一个快乐值,你可以邀请无限多的人,但是相邻两级不能同时邀请。
(例如:如果a是bcd的上级,你邀请了a,就不能再邀请bcd,但却仍然可以邀请bcd的下级,如果你邀请了bcd中的一个,就不能再邀请a)
返回你能获得的最大快乐值
结构定义
每个结点有一个val,储存员工的快乐值,再有一个存放下级的指针数组
class Node
public:
int val;
vector<Node*>next;
;
我们首先还是先分为几种可能性:
- 根结点
- 根结点不去
那我们的信息就可以有两个,一个是根结点不去获得的收益,另一个是根结点去获得的收益,最后的结果在两个信息之间取最大值
- 如果根结点去了,那么就加上下级不去的收益
- 如果根结点不去,下级可以选择去,可以选择不去,这时我们就加上某个下级结点去和不去的最大值
class Node
public:
int val;
vector<Node*>next;
;
以上是关于二叉树DP解题套路的主要内容,如果未能解决你的问题,请参考以下文章
算法进阶面试题05——树形dp解决步骤返回最大搜索二叉子树的大小二叉树最远两节点的距离晚会最大活跃度手撕缓存结构LRU