用RANSAC算法实现干扰严重的直线拟合~
Posted 扫地僧1234
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了用RANSAC算法实现干扰严重的直线拟合~相关的知识,希望对你有一定的参考价值。
1.说到直线拟合,一般是用最小二乘啦,在opencv里面就是用cv.fitLine来完成,首先简单介绍一下该函数:
cv.fitLine(points, distType, param, reps, aeps[, line]) -> line
points:点集坐标
distType:距离度量的方法,有cv.DIST_L2,cv.DIST_L1等等,L2就是距离r平方的一半,L1就是距离r,其它的可以参考opencv官方文档
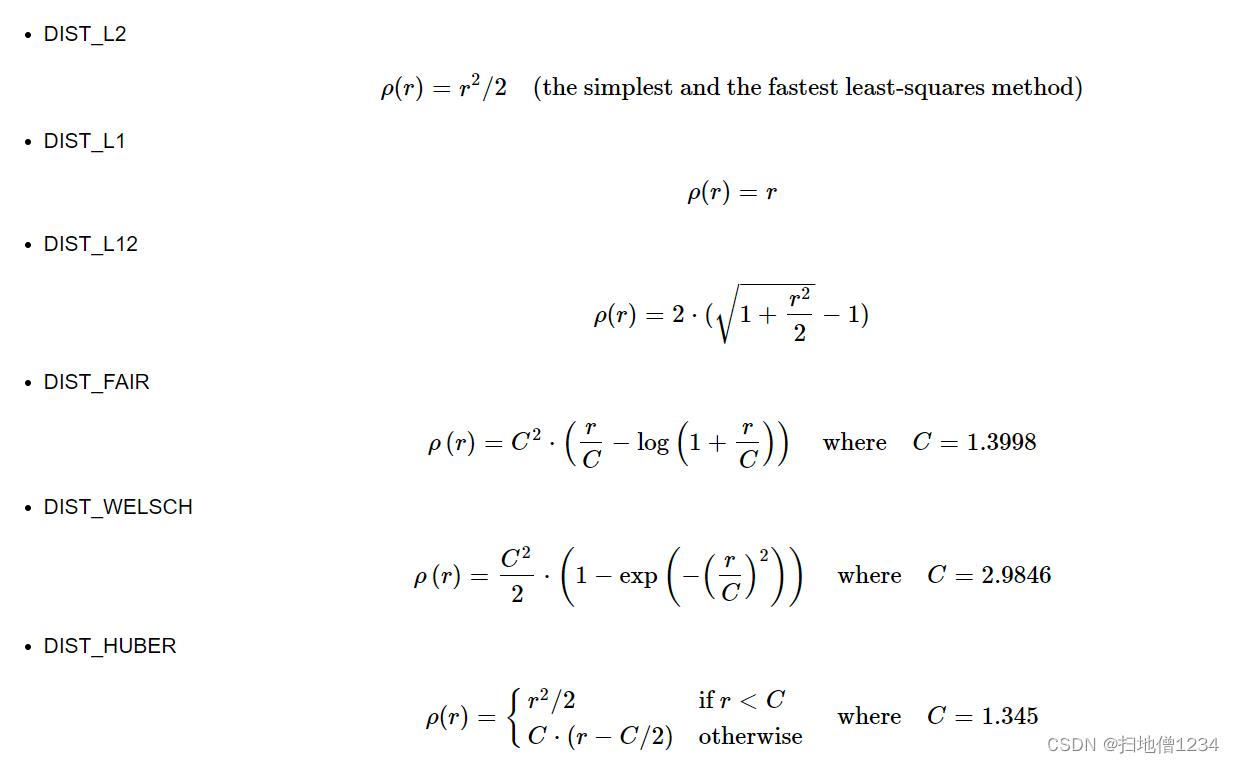
param:就是上图里面的那些c,L1、L2的话就用不到啦,填0即可
reps:原点精度要求(即返回值里面的x,y,也就是直线上的一个点),一般用0.01
aeps:角度精度要求(即返回值里面的vx,vy),一般也用0.01
返回值:vx, vy, x, y。x,y即直线上一个点的坐标,而vy/vx就是斜率,它其实对应的方程如下:
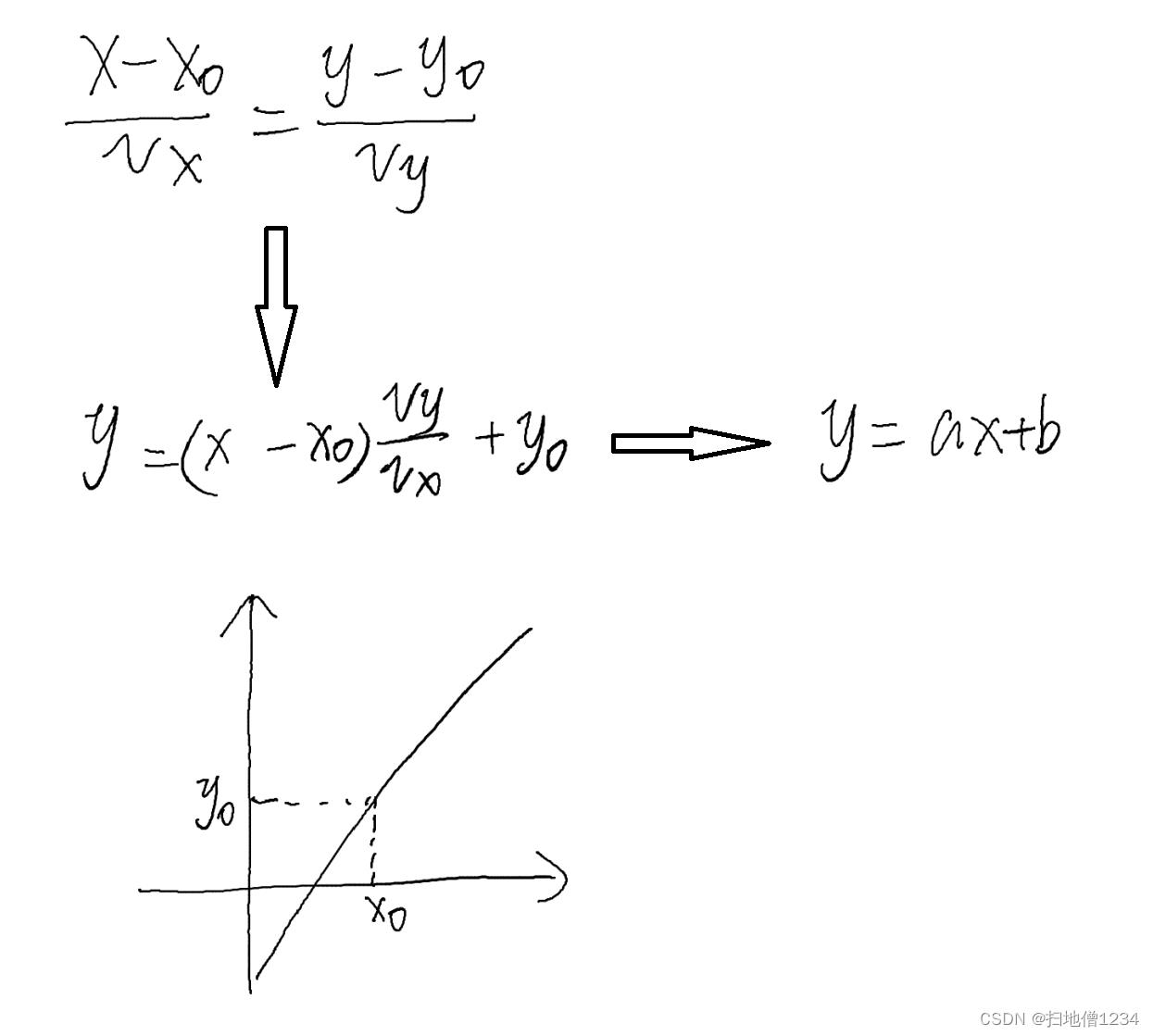
接下来简单试一下:
pts = np.array([[1, 0], [0, 1]])
vx, vy, x, y = cv.fitLine(pts, cv.DIST_L2, 0, 0.01, 0.01)
print('vx = , vy = , x = , y= '.format(vx, vy, x, y))输出结果:vx = [0.70710677], vy = [-0.70710677], x = [0.5], y= [0.5]
如果像下面这样,给坐标再套一层,其实也行,其实这个多套了一层的就是发现轮廓返回的数据格式(即cv.findContours)。
pts = np.array([[[1, 0]], [[0, 1]]])
vx, vy, x, y = cv.fitLine(pts, cv.DIST_L2, 0, 0.01, 0.01)
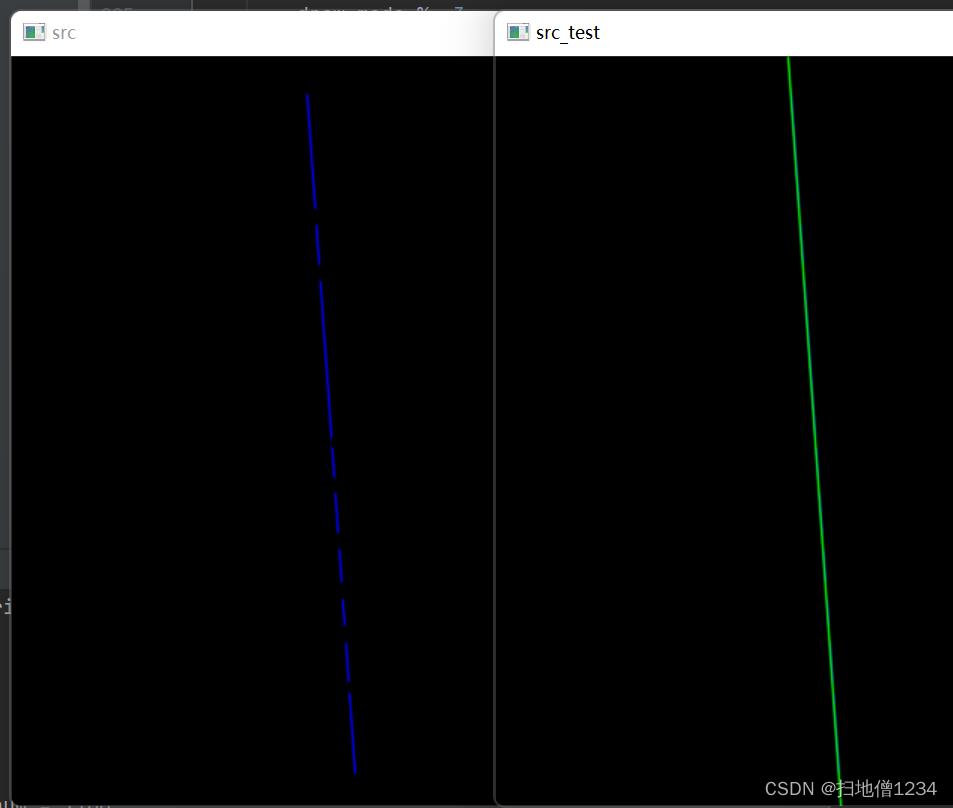
print('vx = , vy = , x = , y= '.format(vx, vy, x, y))2.如果要拟合直线的点集并没有什么干扰那是很简单的,直接用这个函数就行了,比如下图,左边就是我画的一条线,中间再擦除一点东西,其实没有什么干扰,右边就是拟合结果画出来的直线,肯定没什么问题了。
先放上测试代码,没啥好说的,看注释里面的说明:
import cv2 as cv
import numpy as np
import math
import time
src = None
xb = None
yb = None
vx = None
vy = None
draw_mode = 0
def fitline_callback(event, x, y, flags, param):
global xb, yb, src, draw_mode, vx, vy
if xb == x or yb == y:
return
# 模式0:画直线,模式1:橡皮擦,点一下擦个圆,模式2:直线拟合
if event == cv.EVENT_MBUTTONDOWN:
draw_mode += 1
draw_mode %= 3
return
if draw_mode == 0:
if event == cv.EVENT_LBUTTONDOWN:
xb = x
yb = y
elif event == cv.EVENT_LBUTTONUP:
cv.line(src, (xb, yb), (x, y), (255, 0, 0), 1, cv.LINE_AA)
cv.imshow('src', src)
elif draw_mode == 1:
if event == cv.EVENT_LBUTTONDOWN:
cv.circle(src, (x, y), 5, (0, 0, 0), -1, cv.LINE_AA)
cv.imshow('src', src)
elif draw_mode == 2:
if event == cv.EVENT_LBUTTONDOWN:
src_test = np.copy(src)
gray = cv.cvtColor(src_test, cv.COLOR_BGR2GRAY)
# 这边就是获得图上像素值不为0的点集坐标,为啥是::-1?因为行号是y坐标,列数是x坐标,得倒过来才行啦。
# x,y是分开的,所以得用dstack把它们拼起来,这个跟torch.cat差不多哦,不明白的话可以看我的上一篇博客~~
pts = np.dstack(np.where(gray > 0)[::-1]).reshape(-1, 2)
start_time = time.time()
vx, vy, x, y = cv.fitLine(pts, cv.DIST_L2, 0, 0.01, 0.01)
end_time = time.time()
print("耗时秒".format((end_time - start_time)))
lefty = int((-x * vy / vx) + y) # 这个就是x=0时,y是多少
righty = int(((src.shape[1] - x) * vy / vx) + y) # 这个是x等于图像宽度时,y是多少,参考我上面那个直线方程的图就明白了
cv.line(src_test, (src.shape[1] - 1, righty), (0, lefty), (0, 255, 0), 1, cv.LINE_AA)
cv.imshow('src_test', src_test)
def fitline_test():
global src
src = np.zeros((500, 800, 3), dtype=np.uint8)
cv.namedWindow('src', cv.WINDOW_AUTOSIZE)
cv.imshow('src', src)
cv.setMouseCallback('src', fitline_callback, None)
cv.waitKey(0)
cv.destroyAllWindows()
if __name__ == '__main__':
fitline_test()
接下来加了一些干扰进去,发现就不行了。
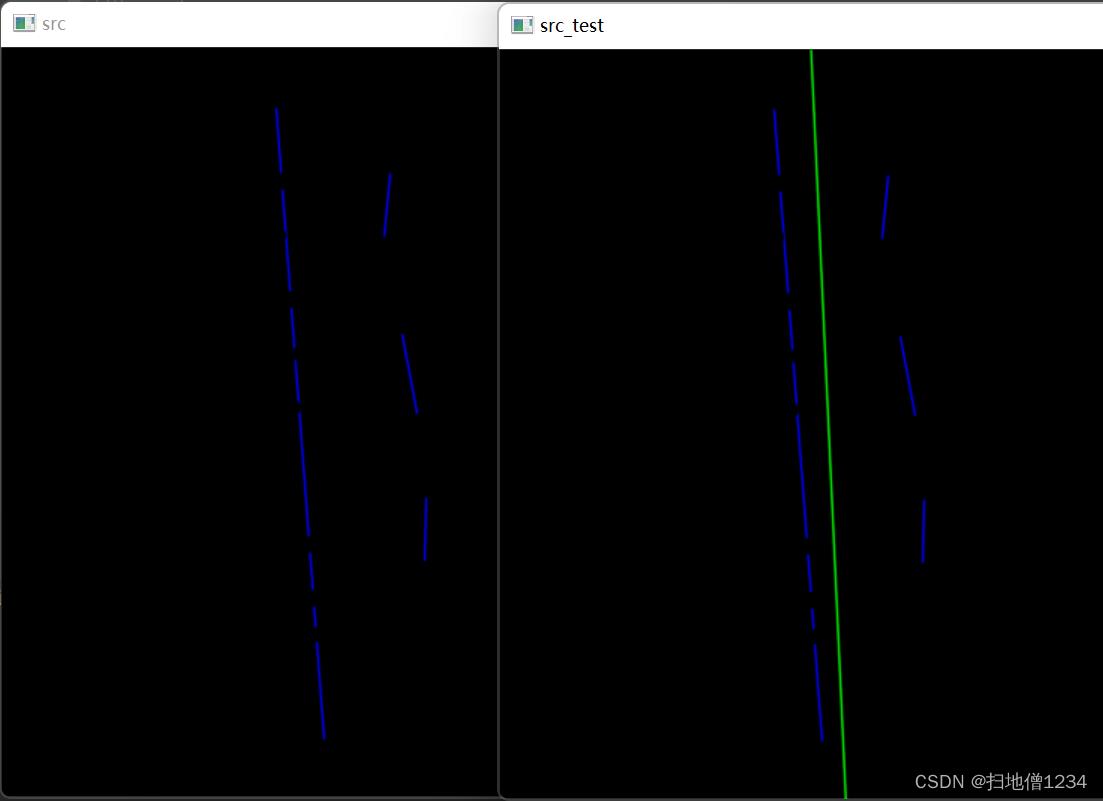
2.那么有什么办法能把那些干扰去掉呢,这里就用一个叫做“随机抽样一致性(RANSAC)”的算法,首先声明一下:这个方法好不好用不敢说,如果有什么更好的方法欢迎在评论区指点。
首先说两个名词:
局内项:即都是在主要的那条直线上的点
局外项:即干扰项,或者说是错误项
假设局内项占总数百分比为w,我一次随机抽选n个点进行拟合,那么n个点都是局内项的概率就是w^n(w的n次方,这里就用^表示次方了)
n个点里至少有一个是局外项的概率(其实就是有局外项的概率啦)即1-w^n
一共尝试k次,即第一次选n个点拟合一下,第二次再选n个点拟合一下,。。。直到第k次,那么这k次都有局外项的概率就是(1-w^n)^k
所以k次里面至少有一次没有局外项的概率就是1-(1-w^n)^k,即置信概率c,稍微有那么一点点绕哈,一步步想就想明白了,这个概论就是我们最终要的概率,我们要求不高,我们就指望这k次里面出现一次都是局内项就行了,这个概率越高,我们的成功率就越高了,所以在实际使用过程中,我们可以把c设高一点,比如设为0.98,即98%
等等,还并没有说完,k次里面出现了一次全是局内项的情况有啥用呢?我们每一次抽选n个点的时候,用它们拟合直线(就用cv.fitline就蛮好),拟合出来之后,剩余的点(就是没抽选的点)都需要计算一下跟这条直线的距离,如果距离大于阈值(设置的阈值,比如2个像素值),那就是局外项,否则就是局内项,统计局内项的个数,这个个数如果越大,那就说明这次选的n个点就越可能都是局内项。所以呢最终我们要的就是局内项最多的那一次的选择。是不是很有道理的样子!
再等下,还有一个问题没解决,就是这个k到底是多少呢,上面说了c=1-(1-w^n)^k,c、n明显是我们自己决定了,比如置信概率c定为0.98,n就选为2(两点就是一条直线了麻),w我们多半不会知道明确的w值,但我们可以估计啊。比如局外项差不多在10分之1,那w就可以估到0.8(求稳),估0.9其实也可以(算起来更快哦),现在只有k一个变量了,那k就可以解了。不过为了说明我们求解的意义,以及实际我们需要的k到底是比这个解大?还是比这个解小?(其实实际需要抽样的次数肯定是大于等于k了),我们还是演算一下。
直接上图,P就是至少有一次都是局内项的概率,现在P要大于c,解到红框处时,k到底是大于一个值呢,还是小于一个值呢,看图的右边,底数明显小于1,此指数函数如右图所示,函数值y要小于1-C,x明显是要大于一个值了。
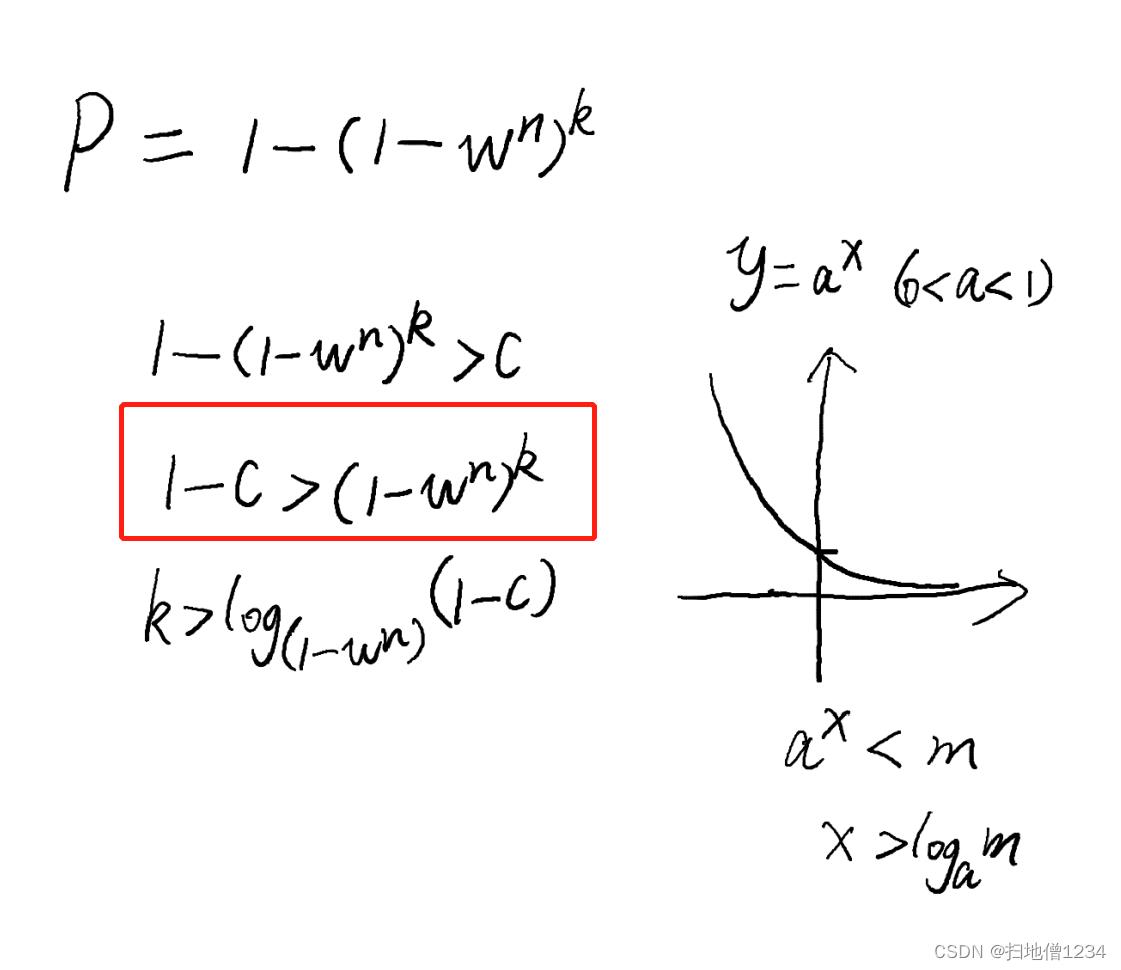
先放一下实验效果,中间就是直接用fitline拟合,右边是用RANSAC算法拟合,效果还不错。
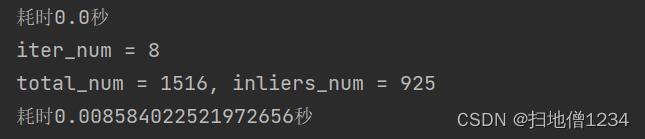
运行时间如下,第一次耗时就是直接用fitline了,第二次耗时是用RANSAC, 我设的c是0.98,w是0.6,抽样点数是2,计算出的k(iter_num)是8,并不需要试多少次,所以蛮快的。
声明一下,不同电脑运行速度不一样啊,白天我用的老古董台式机还要0.05秒的样子,看来那CPU是真不行了。
接下来直接上代码,具体实现跟上面说的完成一样,就是试k次,每次计算局内项,最终采用局内项最多的那一次。直接上全部代码,测试代码有更新(把采用ransac的方法加进去了),ransac拟合直线的函数就是fitline_ransac
import cv2 as cv
import numpy as np
import math
import time
def get_distance_line_and_p_batch(vx, vy, p0, p1_list):
"""
求点到直线距离
:param vx:
:param vy:
:param p0: 线上点
:param p1: 线外点
:return:
"""
# print("vx = , vy = , p0 = , p1 = ".format(vx, vy, p0, p1))
x0, y0 = p0
B0 = [vy * x0 - vx * y0] * len(p1_list)
B1 = [vx * p1[0] + vy * p1[1] for p1 in p1_list]
A = np.array([[vy, -vx], [vx, vy]], dtype=np.float32)
B = np.array([B0, B1], dtype=np.float32)
ret, X = cv.solve(A, B, flags=cv.DECOMP_LU)
x2 = X[0, :]
y2 = X[1, :]
x1 = np.array([p1[0] for p1 in p1_list], dtype=np.float32)
y1 = np.array([p1[1] for p1 in p1_list], dtype=np.float32)
return ((x2 - x1) ** 2 + (y2 - y1) ** 2) ** 0.5, x2, y2
def fitline_ransac(pts, distance, confidence, correct_rate, fit_use_num=2):
"""
拟合直线
:param pts:
:param distance:
:param confidence: 置信度
:param correct_rate: 估计局内项所占比率
:param fit_use_num: 一次拟合所用点数
:return:
"""
iter_num = int(math.log(1 - confidence, 1 - correct_rate ** fit_use_num))
pts = np.float32(pts)
print("iter_num = ".format(iter_num))
inliers = None
inliers_num = 0
for i in range(iter_num):
tmp_pts = pts[np.random.choice(pts.shape[0], fit_use_num)]
tmp_vx, tmp_vy, tmp_x, tmp_y = cv.fitLine(tmp_pts, cv.DIST_L2, 0, 0.01, 0.01)
tmp_vx = tmp_vx[0]
tmp_vy = tmp_vy[0]
tmp_x = tmp_x[0]
tmp_y = tmp_y[0]
tmp_distance, _, _ = get_distance_line_and_p_batch(tmp_vx, tmp_vy, (tmp_x, tmp_y), pts)
tmp_inliers = np.uint8(tmp_distance <= distance) # 小于等于阈值的就是局内项
tmp_inliers_num = np.sum(tmp_inliers)
if inliers_num < tmp_inliers_num: # 如果当前这次抽样的局内项更大,那就采用当前这一次
inliers_num = tmp_inliers_num
inliers = tmp_inliers
# 之前两个点的拟合只是为了排除局外项,再用所有局内项拟合一次,结果更精确
tmp_pts = pts[inliers > 0]
vx, vy, x, y = cv.fitLine(tmp_pts, cv.DIST_L2, 0, 0.01, 0.01)
print("total_num = , inliers_num = ".format(pts.shape[0], inliers_num))
return vx, vy, x, y
src = None
xb = None
yb = None
vx = None
vy = None
draw_mode = 0
def fitline_callback(event, x, y, flags, param):
global xb, yb, src, draw_mode, vx, vy
if xb == x or yb == y:
return
# 模式0:画直线,模式1:橡皮擦,点一下擦个圆,模式2:直线拟合
if event == cv.EVENT_MBUTTONDOWN:
draw_mode += 1
draw_mode %= 3
return
if draw_mode == 0:
if event == cv.EVENT_LBUTTONDOWN:
xb = x
yb = y
elif event == cv.EVENT_LBUTTONUP:
cv.line(src, (xb, yb), (x, y), (255, 0, 0), 1, cv.LINE_AA)
cv.imshow('src', src)
elif draw_mode == 1:
if event == cv.EVENT_LBUTTONDOWN:
cv.circle(src, (x, y), 5, (0, 0, 0), -1, cv.LINE_AA)
cv.imshow('src', src)
elif draw_mode == 2:
if event == cv.EVENT_LBUTTONDOWN:
src_test = np.copy(src)
gray = cv.cvtColor(src_test, cv.COLOR_BGR2GRAY)
# 这边就是获得图上像素值不为0的点集坐标,为啥是::-1?因为行号是y坐标,列数是x坐标,得倒过来才行啦。
# x,y是分开的,所以得用dstack把它们拼起来,这个跟torch.cat差不多哦,不明白的话可以看我的上一篇博客~~
pts = np.dstack(np.where(gray > 0)[::-1]).reshape(-1, 2)
start_time = time.time()
vx, vy, x, y = cv.fitLine(pts, cv.DIST_L2, 0, 0.01, 0.01)
end_time = time.time()
print("耗时秒".format((end_time - start_time)))
lefty = int((-x * vy / vx) + y) # 这个就是x=0时,y是多少
righty = int(((src.shape[1] - x) * vy / vx) + y) # 这个是x等于图像宽度时,y是多少,参考我上面那个直线方程的图就明白了
cv.line(src_test, (src.shape[1] - 1, righty), (0, lefty), (0, 255, 0), 1, cv.LINE_AA)
cv.imshow('src_test', src_test)
src_test = np.copy(src)
start_time = time.time()
vx, vy, x, y = fitline_ransac(pts, 2, 0.98, 0.6, 2)
end_time = time.time()
print("耗时秒".format((end_time - start_time)))
lefty = int((-x * vy / vx) + y)
righty = int(((src.shape[1] - x) * vy / vx) + y)
cv.line(src_test, (src.shape[1] - 1, righty), (0, lefty), (0, 255, 0), 1, cv.LINE_AA)
cv.imshow('src_test1', src_test)
def fitline_test():
global src
src = np.zeros((500, 800, 3), dtype=np.uint8)
cv.namedWindow('src', cv.WINDOW_AUTOSIZE)
cv.imshow('src', src)
cv.setMouseCallback('src', fitline_callback, None)
cv.waitKey(0)
cv.destroyAllWindows()
if __name__ == '__main__':
fitline_test()
还有一点没有具体说的就是:算局内项局外项的时候不是得算点和直线距离吗,这个怎么算?其实很简单啦,求点到直线的垂线的交点,然后算两点距离就是点线距离啦(不过好像还有更简单的哦,可能直接就能得到点线距离的公式,得研究研究~~)。这里就不详述了,求点线距离的函数先直接给到代码里,即get_distance_line_and_p_batch。如果感兴趣,见听下回分解,单独水一篇“点线距离”
以上是关于用RANSAC算法实现干扰严重的直线拟合~的主要内容,如果未能解决你的问题,请参考以下文章