PCL：RANSAC 空间直线拟合

Posted 2021-09-20 没事就要敲代码

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了PCL：RANSAC 空间直线拟合相关的知识，希望对你有一定的参考价值。

文章目录

1 SACMODEL_LINE 模型

空间直线模型，每次采样2个点，返回6个最优模型系数

6个最优模型系数

系数	意义
coefficient[0]	直线上一点的 x 坐标
coefficient[1]	直线上一点的 y 坐标
coefficient[2]	直线上一点的 z 坐标
coefficient[3]	直线方向向量的 x 分量
coefficient[4]	直线方向向量的 y 分量
coefficient[5]	直线方向向量的 z 分量

2 实现代码

代码：

#include <pcl/io/pcd_io.h>
#include <pcl/sample_consensus/ransac.h>
#include <pcl/sample_consensus/sac_model_line.h>
#include <pcl/visualization/pcl_visualizer.h>

using namespace std;

int main()
{
	//------------------------------- 加载点云 -------------------------------
	pcl::PointCloud<pcl::PointXYZ>::Ptr cloud(new pcl::PointCloud<pcl::PointXYZ>);
	if (pcl::io::loadPCDFile("straightLine.pcd", *cloud) < 0)
	{
		PCL_ERROR("\\a点云文件不存在！\\n");
		system("pause");
		return -1;
	}
	cout << "->加载点云个数：" << cloud->points.size() << endl;
	//========================================================================

	//----------------------------- 空间直线拟合 -----------------------------
	pcl::SampleConsensusModelLine<pcl::PointXYZ>::Ptr model_line(new pcl::SampleConsensusModelLine<pcl::PointXYZ>(cloud));	//指定拟合点云与几何模型
	pcl::RandomSampleConsensus<pcl::PointXYZ> ransac(model_line);	//创建随机采样一致性对象
	ransac.setDistanceThreshold(0.01);	//内点到模型的最大距离
	ransac.setMaxIterations(1000);		//最大迭代次数
	ransac.computeModel();				//执行RANSAC空间直线拟合

	vector<int> inliers;				//存储内点索引的向量
	ransac.getInliers(inliers);			//提取内点对应的索引

	/// 根据索引提取内点
	pcl::PointCloud<pcl::PointXYZ>::Ptr cloud_line(new pcl::PointCloud<pcl::PointXYZ>);
	pcl::copyPointCloud<pcl::PointXYZ>(*cloud, inliers, *cloud_line);

	/// 模型参数
	Eigen::VectorXf coefficient;
	ransac.getModelCoefficients(coefficient);
	cout << "直线点向式方程为：\\n"
		<< "   (x - " << coefficient[0] << ") / " << coefficient[3]
		<< " = (y - " << coefficient[1] << ") / " << coefficient[4]
		<< " = (z - " << coefficient[2] << ") / " << coefficient[5];
	//========================================================================

	//---------------------------- 可视化（可选） -----------------------------
	pcl::visualization::PCLVisualizer::Ptr viewer(new pcl::visualization::PCLVisualizer("拟合结果"));

	viewer->setBackgroundColor(1, 1, 1);

	viewer->addPointCloud<pcl::PointXYZ>(cloud, "cloud");													//添加原始点云
	viewer->setPointCloudRenderingProperties(pcl::visualization::PCL_VISUALIZER_COLOR, 1, 0, 0, "cloud");	//颜色
	viewer->setPointCloudRenderingProperties(pcl::visualization::PCL_VISUALIZER_POINT_SIZE, 5, "cloud");	//点的大小

	viewer->addPointCloud<pcl::PointXYZ>(cloud_line, "line");												//添加拟合点云
	viewer->setPointCloudRenderingProperties(pcl::visualization::PCL_VISUALIZER_COLOR, 0, 0, 0, "line");	//颜色
	viewer->setPointCloudRenderingProperties(pcl::visualization::PCL_VISUALIZER_POINT_SIZE, 5, "line");		//点的大小

	while (!viewer->wasStopped())
	{
		viewer->spinOnce(100);
		boost::this_thread::sleep(boost::posix_time::microseconds(100000));
	}
	//========================================================================

	return 0;
}

输出结果：

->加载点云个数：55
直线点向式方程为：
   (x - 2.72611) / 0.57735 = (y - 1.36255) / 0.57735 = (z - 3.71509) / 0.57735

3 结果展示

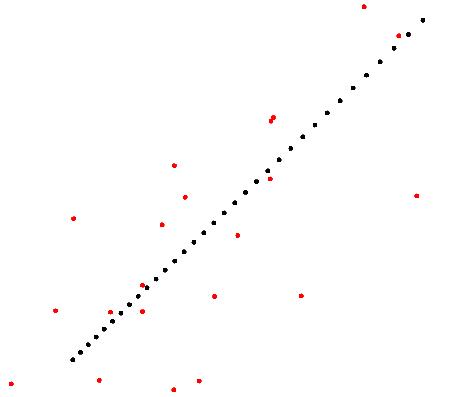
4 源码

template <typename PointT> bool
pcl::SampleConsensusModelLine<PointT>::computeModelCoefficients (
      const std::vector<int> &samples, Eigen::VectorXf &model_coefficients)
{
  // Need 2 samples
  if (samples.size () != 2)
  {
    PCL_ERROR ("[pcl::SampleConsensusModelLine::computeModelCoefficients] Invalid set of samples given (%lu)!\\n", samples.size ());
    return (false);
  }

  if (fabs (input_->points[samples[0]].x - input_->points[samples[1]].x) <= std::numeric_limits<float>::epsilon () && 
      fabs (input_->points[samples[0]].y - input_->points[samples[1]].y) <= std::numeric_limits<float>::epsilon () && 
      fabs (input_->points[samples[0]].z - input_->points[samples[1]].z) <= std::numeric_limits<float>::epsilon ())
  {
    return (false);
  }

  model_coefficients.resize (6);
  model_coefficients[0] = input_->points[samples[0]].x;
  model_coefficients[1] = input_->points[samples[0]].y;
  model_coefficients[2] = input_->points[samples[0]].z;

  model_coefficients[3] = input_->points[samples[1]].x - model_coefficients[0];
  model_coefficients[4] = input_->points[samples[1]].y - model_coefficients[1];
  model_coefficients[5] = input_->points[samples[1]].z - model_coefficients[2];

  model_coefficients.template tail<3> ().normalize ();
  return (true);
}