2021年第十二届蓝桥杯大赛省赛python大学组真题加解析（更新中）

Posted dlz456

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了2021年第十二届蓝桥杯大赛省赛python大学组真题加解析（更新中）相关的知识，希望对你有一定的参考价值。

目录

1.试题A：卡片

2. 试题B：直线

3. 试题C：货物摆放

4. 试题D：路径 

5. 回路计数

8. 试题H：左孩子右兄弟

9. 试题I：异或数列

10. 试题J：括号序列

11. 空间

12. 跳跃

13. 受伤的皇后（2021模拟题）

14. 删除字符

15. 相乘

16. 灌溉（模拟赛赛题）

17. 扫雷

18. 双向排序

19. 谈判

20.最少砝码

21. 距离和

22.时间加法（模拟题）

23. 排列小球

24. 序列个数

25. 合法日期

26. 图像模糊

27. 数字位数

28. 时间显示

1.试题A：卡片

思路：0-9每个数字各有2021张，1肯定是用得最快的，就是计算从1到某个数字之间共有2021个数字1

代码：

s=0
for i in range(1,5000):
      s=s+str(i).count('1')
      if s==2021:
            print(i)
            break

最后答案：3181

2. 试题B：直线

 思路：(借鉴别人的思路）自己一开始还在想怎么用y=kx+b的形式来表示直线，这种形式的竖直直线没办法求斜率，还要考虑特殊情况。后来看到网上有大佬说可以用两点式直线方程：
(y1-y2) * x +(x2-x1) * y +( x1 * y2 - x2 * y1)=0

最后算出的结果是Ax+By+C=0的格式，只要约分后的A、B、C不相同即可视为不同直线。

代码：

dian=[]
for i in range(0,20):
      for j in range(0,21):
            dian.append((i,j))
result=set()
def gys(x,y):#求x,y的最大公约数
      if y==0:
            return x
      return gys(y,x%y)

for i in range(len(dian)-1):
      x1,y1=dian[i]
      for j in range(i+1,len(dian)):
            x2,y2=dian[j]
            a=y1-y2
            b=x2-x1
            c=x1*y2-x2*y1
            k=gys(gys(a,b),c)
            result.add((a/k,b/k,c/k))

print(len(result))

set()集合本身具有不重复的特点。

对于set()集合，向其中添加元素应该用add函数。和append区分开。

3. 试题C：货物摆放

 思路：L,W,H都是n的因数，所以先求出n的所有因数，放到数列里面。然后对数列的所有数进行一个三层循环，看看有多少种符合条件的方案。

代码：

import math
n = 2021041820210418
fac = []
for i in range(1, int(math.sqrt(n)) + 1):
    if n % i == 0:
        fac.append(i)
        fac.append(int(n / i))
     
x = 0
for l in fac:
    for k in fac:
        for m in fac:
            if l * k * m == n:
                x = x + 1
print(x)

4. 试题D：路径 

思路：本题采用动态规划的思想。dp[i]表示结点1和结点i之间的最短路径长度。

代码：

dp=[float('inf')]*2022

def gbs(x,y):#求x和y的最小公倍数
      x1=x
      y1=y
      while y:
            x,y=y,x%y
      return (x1*y1//x)

for i in range(1,22):
      dp[i]=i

for i in range(22,2022):
      for j in range(1,22):
            dp[i]=min(dp[i],dp[i-j]+gbs(i,i-j))

print(dp[2021])

答案：10266837

5. 回路计数

参考这个：(143条消息) 2021年第十二届蓝桥杯软件类省赛python组试题及其解析。_Kinght_123的博客-CSDN博客_2021蓝桥杯python

6. 试题F：时间显示

 代码：

n=int(input())
a=24*60*60*1000
c=n%a
hour=c//(60*60*1000)
minu=(c%(60*60*1000))//(60*1000)
sec=(c%(60*1000))//1000
print('%02d'%hour,end=':')
print('%02d'%minu,end=':')
print('%02d'%sec,end='')

 7. 试题G：杨辉三角形

 

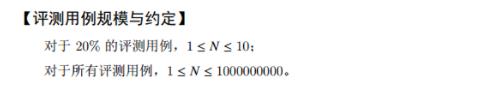
 思路参考：(156条消息) 备战蓝桥杯历年试题：杨辉三角形 省赛B组 Python详解_m0_62277756的博客-CSDN博客

代码：

n=int(input())

def c(a,b):
      res=1
      i,j=a,1
      while j<=b:
            res=res*i/j
            i-=1
            j+=1
      return int(res)
      
def find(j,n):
      l=2*j
      r=n
      while l<=r:
            mid=(l+r)//2
            if c(mid,j)==n:
                  print(int(mid*(mid+1)/2)+j+1)
                  return True
            elif c(mid,j)>n:
                  r=mid-1
            
            else:
                  l=mid+1
      return False
     
      
for i in range(16,-1,-1):
      if find(i,n):
            break

8. 试题H：左孩子右兄弟

 

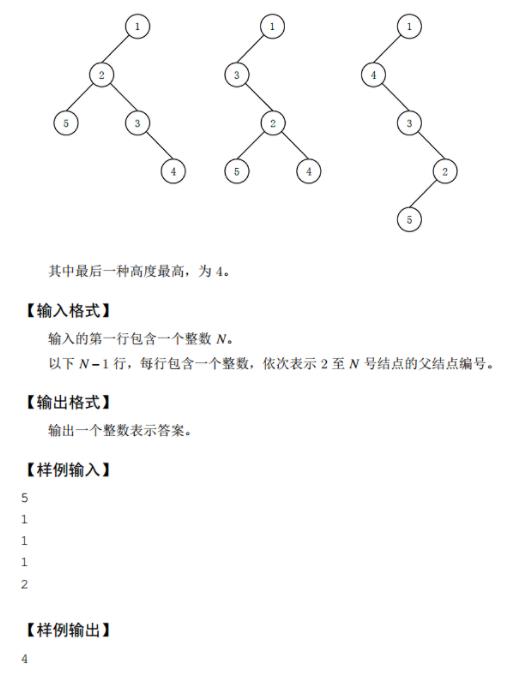
 代码：（运行成功，代码是看的蓝桥官网上别人发的）

import sys
sys.setrecursionlimit(1000000)
n=int(input())
global ans
ans=0
def dfs(u):
    global ans
    tot=len(s[u])
    for i in range(tot):
        v=s[u][i]
        f[v]=f[u]+tot
        ans=max(ans,f[v])
        dfs(v)
s=[[] for i in range(n+1)]
f=[0]*(n+1)
for i in range(n-1):s[int(input())].append(i+2)
dfs(1)
print(ans)

9. 试题I：异或数列

10. 试题J：括号序列

11. 空间

 这个挺简单的：1MB=1024KB  1KB=1024B 1B=8bit

代码：

a=256*1024*1024*8//32
print(a)

12. 跳跃

题目描述

小蓝在一个 n行 m 列的方格图中玩一个游戏。

开始时，小蓝站在方格图的左上角，即第 1 行第 1 列。

小蓝可以在方格图上走动，走动时，如果当前在第 r 行第 c 列，他不能走到行号比 r 小的行，也不能走到列号比 c 小的列。同时，他一步走的直线距离不超过 3。

例如，如果当前小蓝在第 3 行第 5 列，他下一步可以走到第 3 行第 6 列、第 3 行第 7 列、第 3 行第 8 列、第 4 行第 5 列、第 4 行第 6 列、第 4 行第 7 列、第 5 行第 5 列、第 5 行第 6 列、第 6 行第 5 列之一。

小蓝最终要走到第 n 行第 m 列。

在图中，有的位置有奖励，走上去即可获得，有的位置有惩罚，走上去就要接受惩罚。奖励和惩罚最终抽象成一个权值，奖励为正，惩罚为负。

小蓝希望，从第 1 行第 1 列走到第 n 行第 m 列后，总的权值和最大。请问最大是多少？

输入描述

输入的第一行包含两个整数 n, m，表示图的大小。

接下来 n 行，每行 m 个整数，表示方格图中每个点的权值。

其中，1≤n≤100，−10**4≤权值≤10**4。

输出描述

输出一个整数，表示最大权值和。

输入输出样例

示例 1

输入

3 5
-4 -5 -10 -3 1
7 5 -9 3 -10
10 -2 6 -10 -4

输出

15

运行限制

  • 最大运行时间：1s
  • 最大运行内存: 128M

思路：这个题采用动态规划的思想来解答，跟这篇文章上面第四题路径那个题目是差不多的。

做这个题目我认为有两点比较重要。一是想明白初始条件，二是确定状态转移方程。

通过读题，我们得到的题目条件为：如下图，从白点区域可以一步跳到对勾区域。

因此反过来说也就是：对于下面这个图，想要去到白点区域，可以从这些对勾区域一步跳过去。

假设题目所给的各个点的权值存储在w这个二位列表当中，二维列表dp存储的是从第一行第一列那个点走到当前点的最大值。

那么初始条件dp[0][0]=w[0][0]

然后就是确定状态转移方程：dp[i][j]=max(dp[i][j],dp[i-1][j-b])

代码：

n,m=map(int,input().split())
w=[]
for i in range(n):
    w.append(list(map(int,input().split())))
dp=[[0 for i in range(m)] for j in range(n)]
dp[0][0]=w[0][0]
for i in range(0,n):
    for j in range(0,m):
        for a in range(0,4):
            for b in range(0,4-a):
                if i-a>=0 and j-b>=0:
                    dp[i][j]=max(dp[i][j],dp[i-a][j-a]+w[i-a][j-a])
print(dp[n-1][m-1])

       这个题的代码我是仿照第四题来写的，第四题的初始条件是前22个数的dp都是直接赋值，1和那个数的最小公倍数。我做这个题也没多想，一开始直接把起点能一步跳过去的位置的dp值全都赋值w了，后来一想不对。人家第四题本身就是经过思考，确定了前22个数的dp就是1和它本身的最小公倍数，这就是最优解，才赋值的。。这个题的w可是有正有负，又没让求步数最小，还没准跳几步才能得到权值最小值呢。

13. 受伤的皇后（2021模拟题）

题目描述

有一个 n×n 的国际象棋棋盘（n 行n 列的方格图），请在棋盘中摆放 n 个受伤的国际象棋皇后，要求：

  1. 任何两个皇后不在同一行。
  2. 任何两个皇后不在同一列。
  3. 如果两个皇后在同一条 45 度角的斜线上，这两个皇后之间行号的差值至少为 3 。

请问一共有多少种摆放方案。

输入描述

输入的第一行包含一个整数 n。

其中，1≤n≤10。

输出描述

输出一个整数，表示答案。

输入输出样例

示例 1

输入

4

输出

2

运行限制

  • 最大运行时间：1s
  • 最大运行内存: 128M

代码：这个代码我是看的蓝桥官网上的的一个题解代码

n=int(input())
b=0
def queen(A,row=0):
  global b
  if row==len(A):
    b+=1
  else:
    for wid in range(len(A)):
      A[row]=wid
      flag=True
      for hei in range(row):
        if wid==A[hei]:
          flag=False
        elif abs(hei-row)==abs(wid-A[hei]):
          if abs(hei-row)<3:
            flag=False
      if flag:
        queen(A,row+1)

queen([None]*n)
print(b)

思路解析：A是一个含有n个数的一维列表，Ai=a表示第i行的皇后放在这一行第a列的位置。这样在检查皇后排列的时候，检查是否皇后在同一列这个限制条件就特别方便。

14. 删除字符

题目描述

给定一个单词，请问在单词中删除 t个字母后，能得到的字典序最小的单词是什么？

输入描述

输入的第一行包含一个单词，由大写英文字母组成。

第二行包含一个正整数 t。

其中，单词长度不超过 100，t 小于单词长度。

输出描述

输出一个单词，表示答案。

输入输出样例

示例 1

输入

LANQIAO
3

输出

AIAO

运行限制

  • 最大运行时间：1s
  • 最大运行内存: 128M

思路：用贪心思想来做，题目让删除t个字母，每次删除一个字母得到当前字典序最小的单词都是下一步删除字母的中间过程。

对于删除哪个字母，对于该单词从前往后遍历，只要左边字母的字典序大于右边字母的字典序，那么就删除这个左边字母。

代码：

s=list(input())
t=int(input())

for j in range(t):
    index=0
    while s[index]<=s[index+1]:
        index=index+1
    
    s.remove(s[index])
print(''.join(s))

15. 相乘

本题为填空题，只需要算出结果后，在代码中使用输出语句将所填结果输出即可。

 小蓝发现，他将 1至 1000000007 之间的不同的数与 2021相乘后再求除以 1000000007 的余数，会得到不同的数。 小蓝想知道，能不能在 1 至 1000000007 之间找到一个数，与 2021 相乘后 再除以 1000000007 后的余数为 999999999。如果存在，请在答案中提交这个数； 如果不存在，请在答案中提交 0。

这个就比较简单，直接暴力求解

代码：

for i in range(1,1000000008):
    if i*2021%1000000007==999999999:
        print(i)
        break

16. 灌溉（模拟赛赛题）

题目描述

小蓝负责花园的灌溉工作。

花园可以看成一个 n 行 m 列的方格图形。中间有一部分位置上安装有出水管。

小蓝可以控制一个按钮同时打开所有的出水管，打开时，有出水管的位置可以被认为已经灌溉好。

每经过一分钟，水就会向四面扩展一个方格，被扩展到的方格可以被认为已经灌溉好。即如果前一分钟某一个方格被灌溉好，则下一分钟它上下左右的四个方格也被灌溉好。

给定花园水管的位置，请问 kk 分钟后，有多少个方格被灌溉好？

输入描述

输入的第一行包含两个整数 n,m。

第二行包含一个整数 t，表示出水管的数量。

接下来 t 行描述出水管的位置，其中第 i 行包含两个数 r,c 表示第r行第c 列有一个排水管。

接下来一行包含一个整数 k。

其中，1≤n,m≤100,1≤t≤10,1≤k≤100。

输出描述

输出一个整数，表示答案。

输入输出样例

示例 1

输入

3 6
2
2 2
3 4
1

输出

9

运行限制

  • 最大运行时间：1s
  • 最大运行内存: 128M

这个题比较简单就是用枚举来做

代码：

n,m=map(int,input().split())
t=int(input())
s=[[0 for i in range(m)] for j in range(n)]
s1=[[0 for i in range(m)] for j in range(n)]
for i in range(t):
    x,y=map(int,input().split())
    s[x-1][y-1]=1

k=int(input())
for i in range(k):
    for a in range(n):
        for b in range(m):
            if s[a][b]==1:
                s1[a][b]=1
                if a>0:
                    s1[a-1][b]=1
                if b>0:
                    s1[a][b-1]=1
                if a<n-1:
                    s1[a+1][b]=1
                if b<m-1:
                    s1[a][b+1]=1
                
    s=s1 
print(sum([sum(i) for i in s]))

17. 扫雷

题目描述

在一个 n 行 m 列的方格图上有一些位置有地雷，另外一些位置为空。

请为每个空位置标一个整数，表示周围八个相邻的方格中有多少个地雷。

输入描述

输入的第一行包含两个整数 n,m。

第 2 行到第 n+1 行每行包含 m 个整数，相邻整数之间用一个空格分隔。如果对应的整数为 0，表示这一格没有地雷。如果对应的整数为 1，表示这一格有地雷。

其中，1≤n,m≤100 分钟后还是在当天。

输出描述

输出 n 行，每行 m 个整数，相邻整数之间用空格分隔。

对于没有地雷的方格，输出这格周围的地雷数量。对于有地雷的方格，输出 9。

输入输出样例

示例 1

输入

3 4
0 1 0 0
1 0 1 0
0 0 1 0

输出

2 9 2 1
9 4 9 2
1 3 9 2

运行限制

  • 最大运行时间：1s
  • 最大运行内存: 128M

这个题也很简单，直接两层循环就好

a,b=map(int,input().split())
s=[]
for i in range(a):
    s.append(list(map(int,input().split())))

ans=[[0 for i in range(b)] for j in range(a)]
for i in range(a):
    for j in range(b):
        if s[i][j]==1:
            ans[i][j]=9
        else:
            tmp=0
            for ii in range(-1,2):
                for jj in range(-1,2):
                    if i+ii>=0 and i+ii<a and j+jj>=0 and j+jj<b:
                        tmp=tmp+s[i+ii][j+jj]
            ans[i][j]=tmp
for i in range(a):
    for j in range(b):
        print(ans[i][j],end=' ')
    print()

18. 双向排序

题目描述

给定序列(a1​,a2​,⋅⋅⋅,an​)=(1,2,⋅⋅⋅,n)，即 ai​=i。

小蓝将对这个序列进行 m 次操作，每次可能是将 a1​,a2​,⋯,aqi​​ 降序排列，或者将 aqi​​,aqi+1​​,⋯,an​ 升序排列。

请求出操作完成后的序列。

输入描述

输入的第一行包含两个整数 n,m​，分别表示序列的长度和操作次数。

接下来 m​ 行描述对序列的操作，其中第 i 行包含两个整数 pi​,qi​​ 表示操作类型和参数。当 pi​=0​​ 时，表示将 a1​,a2​,⋅⋅⋅,aqi​​​​ 降序排列；当 pi​=1​ 时，表示将 aqi​​,aqi+1​​,⋯,an​​ 升序排列。

输出描述

输出一行，包含 n 个整数，相邻的整数之间使用一个空格分隔，表示操作完成后的序列。

输入输出样例

示例

输入

3 3
0 3
1 2
0 2

输出

3 1 2

样例说明

原数列为(1,2,3)​​​​​。

第 1​​​​​ 步后为(3,2,1)​​​​​。

第 2​​​​ 步后为(3,1,2)​​。

第 3​​​ 步后为(3,1,2)​。与第 2 步操作后相同，因为前两个数已经是降序了。

评测用例规模与约定

对于 30% 的评测用例，n,m≤1000；

对于 60% 的评测用例，n,m≤5000；

对于所有评测用例，1≤n,m≤100000，0≤pi​≤1，1≤qi​≤n。

运行限制

  • 最大运行时间：2s
  • 最大运行内存: 256M

这个题我用python本身自带的sort函数进行排序的话，时间会超限

下面是时间超限的代码：

n,m=map(int,input().split())
s=[]
for i in range(m):
    p,q=map(int,input().split())
    s.append((p,q))
l=[i for i in range(1,n+1)]
for i in range(m):
    p,q=s[i]    
    if p==0:
        tmp=l[0:q]       
        tmp.sort(reverse=True)       
        l=tmp+l[q:]       
    else:
        tmp=l[q-1:]        
        tmp.sort()        
        l=l[0:q-1]+tmp
for i in range(n):
    print(l[i],end=' ')

这个题我在蓝桥杯练习系统没看到有人发布python的题解，，先这样。。后续找到了在更新。

19. 谈判

题目描述

在很久很久以前，有 n 个部落居住在平原上，依次编号为 1 到 n。第 i 个部落的人数为 ti​。

有一年发生了灾荒。年轻的政治家小蓝想要说服所有部落一同应对灾荒，他能通过谈判来说服部落进行联合。

每次谈判，小蓝只能邀请两个部落参加，花费的金币数量为两个部落的人数之和，谈判的效果是两个部落联合成一个部落（人数为原来两个部落的人数之和）。

输入描述

输入的第一行包含一个整数 n，表示部落的数量。

第二行包含 n 个正整数，依次表示每个部落的人数。

其中，1≤n≤1000，1≤ti​≤104。

输出描述

输出一个整数，表示最小花费。

输入输出样例

示例 1

输入

4
9 1 3 5

输出

31

运行限制

  • 最大运行时间：1s
  • 最大运行内存: 128M

思路：这个也很简单，每次找人数最少的两个部落进行谈判即可

代码：

n=int(input())
s=list(map(int,input().split()))
result=0
s.sort()
for i in range(n-1):
    ans=s[0]+s[1]
    result=result+ans
    s.pop(0)
    s.pop(0)
    s.append(ans)
    s.sort()

print(result)

20.最少砝码

这个我之前写过题解：

(142条消息) 蓝桥杯备赛：贪心_睡会dd的博客-CSDN博客

21. 距离和

题目描述

本题为填空题，只需要算出结果后，在代码中使用输出语句将所填结果输出即可。

两个字母之间的距离定义为它们在字母表中位置的距离。例如 A 和 C 的距离为 2，L 和 Q 的距离为 5。

对于一个字符串，我们称字符串中两两字符之间的距离之和为字符串的内部距离。

例如：ZOO 的内部距离为 22，其中 Z 和 O 的距离为 11。

请问，LANQIAO 的内部距离是多少？

运行限制

  • 最大运行时间：1s
  • 最大运行内存: 128M

代码：

s='LANQIAO'
ans=0
for i in range(6):
    for j in range(i+1,7):
        ans=abs(ord(s[i])-ord(s[j]))+ans

print(ans)

这个题很简单，唯一需要记住的是ord函数以一个字符（长度为1的字符串）作为参数，返回对应的 ASCII 数值，或者 Unicode 数值。

同时提一下chr函数，chr() 用一个范围在 range（256）内的（就是0～255）整数作参数，返回一个对应的字符。

22.时间加法（模拟题）

题目描述

现在时间是 a 点 b 分，请问 t 分钟后，是几点几分？

输入描述

输入的第一行包含一个整数 a。

第二行包含一个整数 b。

第三行包含一个整数 t。

其中0≤a≤23,0≤b≤59,0≤t,t 分钟后还是在当天。

输出描述

输出第一行包含一个整数，表示结果是几点。

第二行包含一个整数，表示结果是几分。

输入输出样例

示例 1

输入

3
20
165

输出

6
5

运行限制

  • 最大运行时间：1s
  • 最大运行内存: 128M

代码：

a=int(input())
b=int(input())
t=int(input())
a=a+(b+t)//60
if a>23:
    a=a-24
b=(b+t)%60
print(a)
print(b)

23. 排列小球

题目描述

小蓝有黄绿蓝三种颜色的小球，分别为 R,G,B 个。同样颜色的小球没有区别。

小蓝将这些小球从左到右排成一排，排完后，将最左边的连续同色小球个数记为 t1​，将接下来的连续小球个数记为 t2​，以此类推直到最右边的小球。

请问，总共有多少总摆放小球的方案，使得 t1​,t2​,⋯ 为严格单调递增序列，即 t1​≤t2​≤t3​≤⋯。

输入描述

输入一行包含三个整数 R,G,B。

其中，0≤R,G,B≤50。。

输出描述

输出一个整数，表示答案。

输入输出样例

示例 1

输入

3 6 0

输出

3

样例说明

用 r 表示红球，g 表示绿球，可能的方案包括：

rrrgggggg

grrrggggg

ggrrrgggg

运行限制

  • 最大运行时间：1s
  • 最大运行内存: 128M

代码：这个是看的蓝桥官网别人发的

r,g,b=[int(x)for x in input().split(' ')]

S=0
def dfs(r,g,b,i,c):
  global S
  if r==0 and g==0 and b==0:
    S+=1
    return True
  if r>i and c!='r':
    for j in range(i,r+1):
      if j>i:
        dfs(r-j,g,b,j,'r')
  if g>i and c!='g':
    for j in range(i,g+1):
      if j>i:
        dfs(r,g-j,b,j,'g')
  if b>i and c!='b':
    for j in range(i,b+1):
      if j>i:
        dfs(r,g,b-j,j,'b')  
  return False


dfs(r,g,b,0,'')
print(S)

24. 序列个数

题目描述

本题为填空题，只需要算出结果后，在代码中使用输出语句将所填结果输出即可。

请问有多少个序列满足下面的条件：

  1. 序列的长度为 5。
  2. 序列中的每个数都是 1 到 10 之间的整数。
  3. 序列中后面的数大于等于前面的数。

代码：

count=0
for a in range(1,11):
    for b in range(a,11):
        for c in range(b,11):
            for d in range(c,11):
                for e in range(d,11):
                    count+=1

print(count)

答案：2002

25. 合法日期

题目描述

小蓝正在上小学，老师要求同学们在暑假每天记日记。可是小蓝整个暑假都在玩，直到最后一天才想起要记日记。于是小蓝赶紧编了一些日记交给老师。

没想到，日记很快就被老师发现了问题，原来小蓝记完 8 月 31 日的日记，竟又记了 8 月 32 日和 8 月 33 日的日记。这显然是有问题的，因为根本没有 8 月 32 日和 8 月 33 日。

给定一个月份和一个日期，请问 2021 年有没有这一天。

输入描述

输入的第一行包含一个整数 m，表示月份。

第二行包含一个整数 d，表示日期。

其中，1≤m≤20，1≤d≤40。

输出描述

如果2021年有 m 月 d 日，输入 yes，否则输出 no。

输入输出样例

示例 1

输入

8
32

输出

no

示例 2

输入

2
28

输出

yes

代码：

import datetime
m=int(input())
d=int(input())
try:
    a=datetime.date(2021,m,d)
    print('yes')
except:
    print('no')

这次用到了datetime模块，把这个模块的其他函数也学习一下：

Python datetime模块详解 - Awakenedy - 博客园 (cnblogs.com)

26. 图像模糊

题目描述

小蓝有一张黑白图像，由 n×m 个像素组成，其中从上到下共 n 行，每行从左到右 m 列。每个像素由一个 0 到 255 之间的灰度值表示。

现在，小蓝准备对图像进行模糊操作，操作的方法为：

对于每个像素，将以它为中心 3×3 区域内的所有像素（可能是 9 个像素或少于 9 个像素）求和后除以这个范围内的像素个数（取下整），得到的值就是模糊后的结果。

请注意每个像素都要用原图中的灰度值计算求和。

输入描述

输入的第一行包含两个整数 n,m。

第 2 行到第n+1 行每行包含 m 个整数，表示每个像素的灰度值，相邻整数之间用一个空格分隔。

其中，1≤n,m≤100 。

输出描述

输出 n 行，每行 m 个整数，相邻整数之间用空格分隔，表示模糊后的图像。

输入输出样例

示例 1

输入

3 4
0 0 0 255
0 0 255 0
0 30 255 255

输出

0 42 85 127
5 60 116 170
7 90 132 191

运行限制

  • 最大运行时间：1s
  • 最大运行内存: 128M

代码：

import math
n,m=map(int,input().split())
s=[]
for i in range(n):
    s.append(list(map(int,input().split())))
s1=[[0 for i in range(m)] for j in range(n)]
for i in range(n):
    for j in range(m):
        count=1
        tmp=s[i][j]
        if i-1>=0 and j-1>=0:
            count=count+1
            tmp=tmp+s[i-1][j-1]        
        if i-1>=0 and j>=0:
            count=count+1
            tmp=tmp+s[i-1][j]
        if i-1>=0 and j+1<=m-1:
            count=count+1
            tmp=tmp+s[i-1][j+1]
        if j-1>=0:
            count=count+1
            tmp=tmp+s[i][j-1]
        if j+1<=m-1:
            count=count+1
            tmp=tmp+s[i][j+1]
        if i+1<=n-1 and j-1>=0:
            count=count+1
            tmp=tmp+s[i+1][j-1]
        if i+1<=n-1 :
            count=count+1
            tmp=tmp+s[i+1][j]
        if i+1<=n-1 and j+1<=m-1:
            count=count+1
            tmp=tmp+s[i+1][j+1]
        s1[i][j]=math.floor(tmp/count)

for i in range(n):
    for j in range(m):
        print(s1[i][j],end=' ')
    print()

python取整函数：

向上取整：math.ceil()

四舍五入：round()

向下取整：math.floor()

向0取整：int()

27. 数字位数

题目描述

本题为填空题，只需要算出结果后，在代码中使用输出语句将所填结果输出即可。

整数 1 到 6 连在一起，成为 123456，长度为 6。

整数 1 到 12 连在一起，成为 123456789101112，长度为 15。

请问整数 1 到 2020 连在一起，长度为多少？

运行限制

  • 最大运行时间：1s
  • 最大运行内存: 128M
count=0
for i in range(1,2021):
    count=count+len(str(i))
print(count)

28. 时间显示

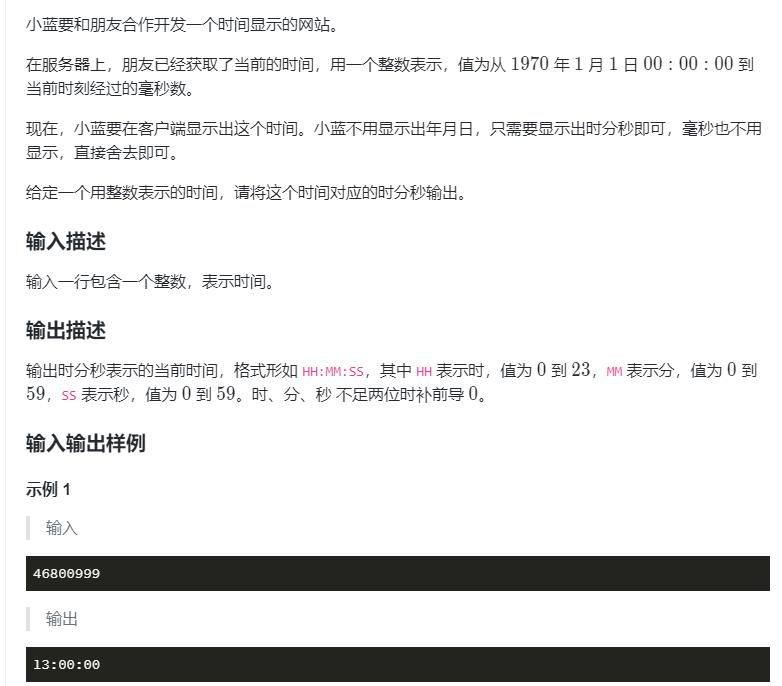
代码：

from datetime import datetime,timedelta
start=datetime(year=1970,month=1,day=1)
dela=timedelta(milliseconds=1)
now=int(input())
now=start+now*dela
print("%02d:%02d:%02d"%(now.hour,now.minute,now.second))

 

2021年第十二届蓝桥杯 - 省赛 - C/C++大学A组 - D.路径

2021年第十二届蓝桥杯 - 省赛 - C/C++大学A组 - D.路径

Ideas

算法：最短路径
数据结构：图
思路：根据规则构图，单源最短路径Dijkstra算法。

首先构图其实很简单，就是按照题目的要求来就可以了，这里需要注意的就是最大公约数和最小公倍数的计算函数，其实可以当做模板背下来了。

def gcd(a, b):
	return a if b == 0 else gcd(b, a % b)


def lcm(a, b):
	return a * b / gcd(a, b)

然后构造图的时候选择通过邻接矩阵的形式去构建。

	graph = [[0] * 2021 for _ in range(2021)]
	for row in range(2021):
		for col in range(2021):
			graph[row][col] = float("inf") if abs(row - col) > 21 else lcm(row + 1, col + 1)

之后就是Dijkstra算法了，简单介绍一下。

Dijkstra单源最短路径算法

松弛操作：对于一对顶点要求最短路径，可以通过中转点将路径变短。

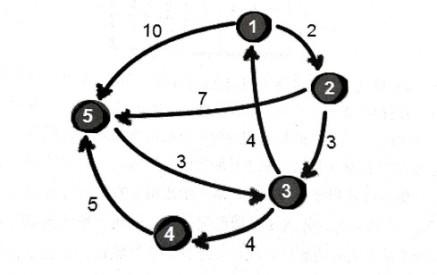
对于i、j两个节点，如果想让路径变短，只能通过第三个节点k来中转。举个例子，从 1->5 距离为10，但 1->2->5 距离变成9了。

单源最短路径问题指的是从一个点出发，求该点到其它所有顶点的最短路径，也就是说，只能计算起点只有一个的情况。

对于图G=<V, E>上带权的单源最短路径问题，Dijkstra算法设置一个集合S用来记录已经求得最短路径的顶点。

初始时把起点v0放入S中，集合S每并入一个新顶点vi，都要修改原点v0到集合V-S中顶点的当前最短路径长度值。


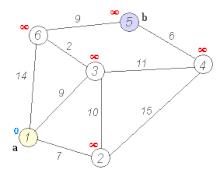
从起点到一个顶点的最短路径一定会经过至少一个“中转点”（我们认为起点也是一个“中转点”），如果我们想要求出起点到一个顶点的最短路径，那我们必须要先求出从起点到中转点的最短路径。

对于图G=<V, E>，将所有的点分为两类，一类是已经确定最短路径的点，称为“红点”，另一类是未确定最短路径的点，称为“白点”。

Dijkstra算法的思想：首先将起点的距离标记为0，而后进行n此循环，每次找出一个到起点距离最短的点，将它从白点变为红点，随后枚举所有的白点，如果以此红点为中转到达某个白点的路径更短的话，那么就更新。

通过Dijkstra最短路径算法可以求得结点1到其它所有结点的最短路径，最后直接输出结点1和节点2021之间的最短路径长度就OK啦。

Code

Python

import heapq


def gcd(a, b):
	return a if b == 0 else gcd(b, a % b)


def lcm(a, b):
	return a * b / gcd(a, b)


def Dijkstra(g, node):
	n, queue, visit = len(g), list(), set()
	heapq.heappush(queue, (0, node))
	distance = [float("inf") for _ in range(n)]
	distance[node] = 0
	
	while queue:
		dist, vertex = heapq.heappop(queue)
		visit.add(vertex)
		
		for i in range(n):
			val = g[vertex][i]
			if val != float("inf") and val not in visit and dist + val < distance[i]:
				distance[i] = dist + val
				heapq.heappush(queue, (dist + val, i))
	return distance


if __name__ == '__main__':
	graph = [[0] * 2021 for _ in range(2021)]
	for row in range(2021):
		for col in range(2021):
			graph[row][col] = float("inf") if abs(row - col) > 21 else lcm(row + 1, col + 1)
	
	dis = Dijkstra(graph, 0)
	print(int(dis[2021 - 1]))

Answer：10266837

以上是关于2021年第十二届蓝桥杯大赛省赛python大学组真题加解析（更新中）的主要内容，如果未能解决你的问题，请参考以下文章

2021年第十二届蓝桥杯 - 省赛 - C/C++大学C组 - D.相乘

2021年第十二届蓝桥杯 - 省赛 - C/C++大学A组 - D.路径

2021 第十二届蓝桥杯大赛软件赛省赛（第二场），C/C++大学B组题解

2021 第十二届蓝桥杯大赛软件赛省赛（第二场），C/C++大学B组题解

2021年第十二届蓝桥杯 - 省赛 - C/C++大学A组 - D.路径

2021年第十二届蓝桥杯大赛软件赛省赛第二场JavaB组C++B组全部题目以及前9题详细题解