2021年第十二届蓝桥杯 - 省赛 - C/C++大学A组 - D.路径

Posted 2022-03-28 Alex_996

2021年第十二届蓝桥杯 - 省赛 - C/C++大学A组 - D.路径

Ideas

算法：最短路径
数据结构：图
思路：根据规则构图，单源最短路径Dijkstra算法。

首先构图其实很简单，就是按照题目的要求来就可以了，这里需要注意的就是最大公约数和最小公倍数的计算函数，其实可以当做模板背下来了。

def gcd(a, b):
	return a if b == 0 else gcd(b, a % b)


def lcm(a, b):
	return a * b / gcd(a, b)

然后构造图的时候选择通过邻接矩阵的形式去构建。

	graph = [[0] * 2021 for _ in range(2021)]
	for row in range(2021):
		for col in range(2021):
			graph[row][col] = float("inf") if abs(row - col) > 21 else lcm(row + 1, col + 1)

之后就是Dijkstra算法了，简单介绍一下。

---

Dijkstra单源最短路径算法

松弛操作：对于一对顶点要求最短路径，可以通过中转点将路径变短。

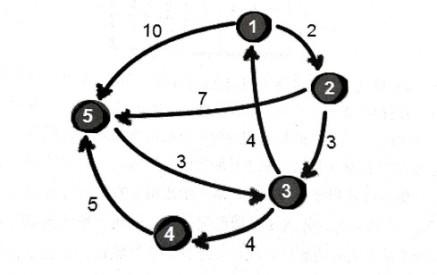
对于i、j两个节点，如果想让路径变短，只能通过第三个节点k来中转。举个例子，从 1->5 距离为10，但 1->2->5 距离变成9了。

单源最短路径问题指的是从一个点出发，求该点到其它所有顶点的最短路径，也就是说，只能计算起点只有一个的情况。

对于图G=<V, E>上带权的单源最短路径问题，Dijkstra算法设置一个集合S用来记录已经求得最短路径的顶点。

初始时把起点v₀放入S中，集合S每并入一个新顶点v_i，都要修改原点v₀到集合V-S中顶点的当前最短路径长度值。

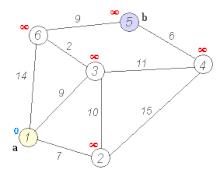
从起点到一个顶点的最短路径一定会经过至少一个“中转点”（我们认为起点也是一个“中转点”），如果我们想要求出起点到一个顶点的最短路径，那我们必须要先求出从起点到中转点的最短路径。

对于图G=<V, E>，将所有的点分为两类，一类是已经确定最短路径的点，称为“红点”，另一类是未确定最短路径的点，称为“白点”。

Dijkstra算法的思想：首先将起点的距离标记为0，而后进行n此循环，每次找出一个到起点距离最短的点，将它从白点变为红点，随后枚举所有的白点，如果以此红点为中转到达某个白点的路径更短的话，那么就更新。

---

通过Dijkstra最短路径算法可以求得结点1到其它所有结点的最短路径，最后直接输出结点1和节点2021之间的最短路径长度就OK啦。

Code

Python

import heapq


def gcd(a, b):
	return a if b == 0 else gcd(b, a % b)


def lcm(a, b):
	return a * b / gcd(a, b)


def Dijkstra(g, node):
	n, queue, visit = len(g), list(), set()
	heapq.heappush(queue, (0, node))
	distance = [float("inf") for _ in range(n)]
	distance[node] = 0
	
	while queue:
		dist, vertex = heapq.heappop(queue)
		visit.add(vertex)
		
		for i in range(n):
			val = g[vertex][i]
			if val != float("inf") and val not in visit and dist + val < distance[i]:
				distance[i] = dist + val
				heapq.heappush(queue, (dist + val, i))
	return distance


if __name__ == '__main__':
	graph = [[0] * 2021 for _ in range(2021)]
	for row in range(2021):
		for col in range(2021):
			graph[row][col] = float("inf") if abs(row - col) > 21 else lcm(row + 1, col + 1)
	
	dis = Dijkstra(graph, 0)
	print(int(dis[2021 - 1]))

Answer：10266837