备战数学建模9-层次分析法模型

Posted 2022-04-29 nuist__NJUPT

层次分析法，简称AHP，是建模比赛中最基础的模型之一，其主要用于解决评价类问题，例如：哪中方案更好？哪位运动员或者员工表现得更优秀？

 

一、层次分析模型建立部分

下面我们看一道引出层次分析得例题，如下所示：

对于上面的题目，我们看样发现是一个评价类问题，解决评价类问题，我们需要想到一下三个问题：

1-评价的目标是什么？

在这里显然是选择目标景点。

2-为了达到目标有几种方案可以选择？

在这里是有3种方案可以选择的。

3-评价的指标或者准则是什么？就是根据什么评价方案的好坏？

从题目中提取，头脑风暴，或者从知网搜相关的指标，也可以在参考文献中引用。

假设我们找到了如下5个指标：旅游景色，旅游花费，居住环境 ，饮食情况，交通便利情况；

对于5个评价指标，我们怎么样分配权重呢，如果直接分配权重往往考虑不周。我们采用的解决方法是；每两个指标进行比较，共比较10次，最终根据两两比较的结果推算出权重。

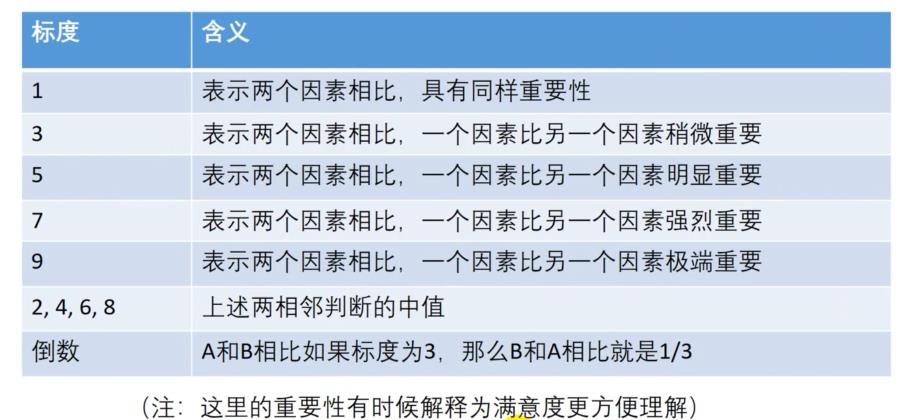
用1-9表示重要程度，两两比较上述5个指标对最终选择旅游经典的重要性。

我们可以询问小明10次，就可以，把如下表格填满。当然需要注意的是：实际情况下，是没有小明帮我们回答，层次分析法中这张表是交给"专家"给我们填的，其实这个专家就是我们自己，哈哈哈，判断矩阵的填写根据题目意思和查资料，判断因素的重要性。

对于上面的表格矩阵，我们称为判断矩阵，我们可以总结如下三点：

下面是关于判断矩阵内部的介绍，在使用判断矩阵求权重之前，我们需要对其进行以执行检验，如如果不一致性过大，判读矩阵就失效了。 

一致性检验原理：检验我们构造的判断矩阵和一致矩阵是否有太大的差别。

一致性检验的步骤如下：

具体地，那么RI是怎么计算得到的呢？

 如果判断矩阵通过一致性检验，那么怎么通过判断矩阵计算权重？

方法1：算数平均法求权重

对于如下判断矩阵，分别使用第1，2，3列计算权重。

对权重进行算术平均：

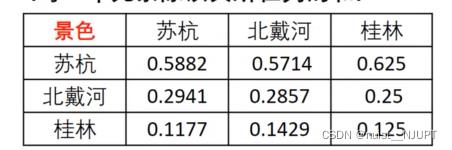
将判断矩阵按照列归一化，就是将求出的权重填入如下表中：

 

将归一化的各列相加，即按行求和，如下所示：

将相加得到的向量每个元素除以n，则得到权重向量，如下所示：

 

上述通过判断矩阵得到的权重向量的过程可以通过如下公式表示：

方法2：几何平均法求权重

具体步骤如下：

方法3：特征值法求权重

一致矩阵有一个特征值为n，其余特征值为0，特征值为n时，对应的特征向量刚好为：

这一特征向量刚好就是矩阵的第一列。

特征值法求权重步骤：

第一，求出判断矩阵的最大特征值及其对应的特征向量。

第二，求出特征向量进行归一化，即可得到我们的权重。

注：正常竞赛中用特征值法求权重就可以。

通过判断矩阵求出权重后，如何计算各个方案的得分呢？如下是每个因素的权重信息：

每个方案的得分就是对应的两列相乘后求和，如下所示：

通过上面的题目我们重新看一下层次分析法：

首先层次分析法，要考虑三个方面，分别为目标、准则、方案；我们要分析系统的各因素之间的关系，建立系统的递阶层次结构。

上述题目的递阶层次结构如下：

数学建模论文中，用到层次分析法，需要给出层次结构。

然后，根据题目数据和搜网上的资料，填写判断矩阵，上述准则层5个因素的判断矩阵如下：

然后，由判断矩阵计算被比较元素相对于该准则的相对权重，并进行一致性检验，检验通过才能用。可以使用三种方法计算权重。

使用三种方法计算权重会保证结果的稳健性。可在论文中加上如下：

对于判断矩阵不一致，可以根据一致性矩阵各行各列呈倍数关系，往一致性矩阵上调。

层次分析法的局限性

 1-评价的决策层不能太多，太多会导致判断矩阵和一致性矩阵偏差太大，RI也求不出。

2-如果决策层的数据是已知的，不适合用层次分析法。

 上面写的有点混乱，看下面总结吧！！！

总结：层次分析法步骤：

1-要考虑三个方面，分别为目标、准则、方案；我们要分析系统的各因素之间的关系，建立系统的递阶层次结构。

2-根据一致矩阵给出判断矩阵，当然这个判断矩阵可以根据题目，也可以网上查找给出。

3-根据判断矩阵使用三种方法求权重，需要做归一化处理。

4-求出权重后进行一致性检验，检验通过，才能使用该权重，也就是判断矩阵给的合理。

5-最后根据权重，计算每个方案的得分，得分越高，则该方案越好。

下面看一下层次分析法的MATLAB代码是实现：

clear; clc
%矩阵A是给出的判断矩阵
A = [1,1,4,1/3,3; 1,1,4,1/3,3; 1/4,1/4,1,1/3,1/2; 3,3,3,1,3; 1/3,1/3,2,1/3,1] ;
%方法1：算数平均法求权重

%第一步：将判断矩阵按照列归一化，即按列求和，让相应元素除以该列的元素和
Sum_A = sum(A,1) ; %按列求和
n = size(A,1) ; %得到矩阵A的行数
SUM_A = repmat(Sum_A,n,1) ; %将按列求和得到的向量重复n次，变成一个n*1的矩阵
stand_A = A ./ SUM_A ; %归一化，就是每个元素除以对应列的和

%第二步，将归一化的各列相加，即按行求和
disp('算术平均法求权重的结果为：') ;
disp(sum(stand_A,2) /  n) ;


%方法2：几何平均法求权重

%第一步，将矩阵A按照行相乘，得到一个列向量
Prduct_A = prod(A,2) ;

%第二步，将新的向量每个值开n次方
Prduct_n_A = Prduct_A .^(1/n) ;

%对该向量进行归一化即可得到权重向量，即将列向量的每一个元素除以列向量的和即可
disp('几何平均法求权重的结果为：') ;
disp(Prduct_n_A ./ sum(Prduct_n_A)) ;

%方法3：特征值法求权重

%第一步：求出矩阵A的最大特征值和其对应的特征向量
[V,D] = eig(A) ; %V是特征向量，D是特征值
Max_eig = max(max(D)) ; %求出最大特征值
[r,c] = find(D==Max_eig, 1) ; %找到最大特征值行和列，找到第一个满足条件的即可

%第二步：对求出的向量进行归一化，即可得到权重
disp('特征值求权重的结果为：') ;
disp(V(:,c) ./ sum(V(:,c))) ;


%计算一致性，一致性检验
CI = (Max_eig - n) / (n - 1) ; %根据公式计算一致性指标
RI = [0,0,0.52,0.89,1.12,1.26,1.36,1.41,1.46,1.49,1.52,1.54,1.56,1.58,1.59] ; %查表就可以，支持最多n=15
CR = CI / RI(n) ; %计算一致性比例
if(CR<0.1)
    disp('判断矩阵A的一致性可以接受！！！') ;
else
    disp('判断矩阵A的一致性不可以接受！！！') ;
end