备战数学建模10-主成分分析模型与因子分析模型
Posted nuist__NJUPT
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了备战数学建模10-主成分分析模型与因子分析模型相关的知识,希望对你有一定的参考价值。
目录
一、主成分分析模型
1-主成分分析基本原理
主成分分析法是利用降维的思想,在损失很少信息的前提下把多个指标转换为几个综合指标的多元统计方法。转换成的综合指标被称为主成分,其中每个主成分都是原始变量的线性组合,且各个主成分之间互不相关,这就使得主成分比原始变量具有某些更优越的性能。
我们看一下基本原理:
我们想要找到c1,c2...cp,使得s1,s2...sn尽可能的分散。
当然我们需要加上某种限制,否则,权重系数无穷大就没有意义了。
一般的限制如下:
正常情况下一个主成分很难表示原来的p个变量,我们应该找到多个相互独立的主成分,统计上说就是让两个主成分协方差为0,几何上说就是两个主成分的方向上正交。具体确定各个主成分的方法如下:
2-主成分分析基本步骤
第1步:将原始数据标准化,以消除量纲的影响(SPSS自动计算)
第2步:建立变量之间的相关系数矩阵R
第3步:计算相关系数矩阵R的特征值和特征向量
第4步:写出主成分并计算综合得分
3-主成分分析的SPSS实现
我们看一下下面的实验案例:
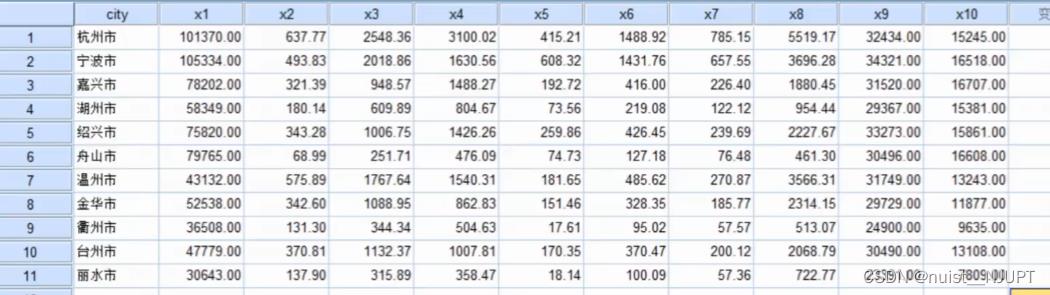
下面是浙江省11座城市的国名经济主要指标,我们需要根据这些指标取计算每个城市的总额和得分。
使用SPSS软件进行分析步骤如下:
1-将excel数据导入SPSS,选择分析->降维->因子分析。
2-将x1,,,x10等10个指标填入变量中。
3-描述中的相关性矩阵选择:系数,KMO和巴特勒特球形度检验
4-抽取(提取)的选项中勾选碎石图。
5-旋转选项中默认是无就可以,可以勾选一下载荷图。
6-选项中勾选按大小排序。
7-点击确定就可以了。
注意:对于度量单位不同的指标或者取值单位彼此相差很大的指标,应该考虑将数据标准化,应该从相关性矩阵出发。对于同度量单位或者取值范围在同一量级的指标是从协方差矩阵出发。
我们看一下SPSS的分析结果:
1-相关性矩阵
主成分分析适用于变量之间有较强的相关性关系,如果原始数据的相关性较弱,使用主成分分析不能起到很好的降维作用,一般认为当原始数据的变量之间的相关系数大部分小于0.3时,使用主成分分析的效果不理想。可以看到上面的变量相关性较强。
2-KMO和Bartlett检验
检验各因素有没有关联程度,一般认为:KMO应大于等于0.6,sig应小于等于0.05.
3-总方差解释和碎石图。
对于10个主成分来说,提取出了两个特征值大于1的主成分,可以解释总方差的91.976.碎石图对应10个指标的特征值。
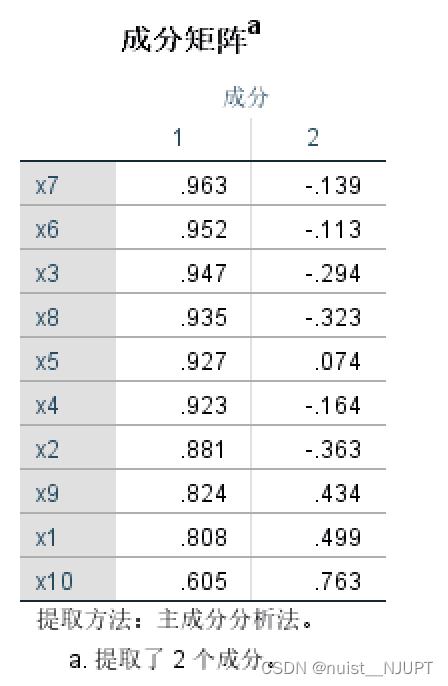
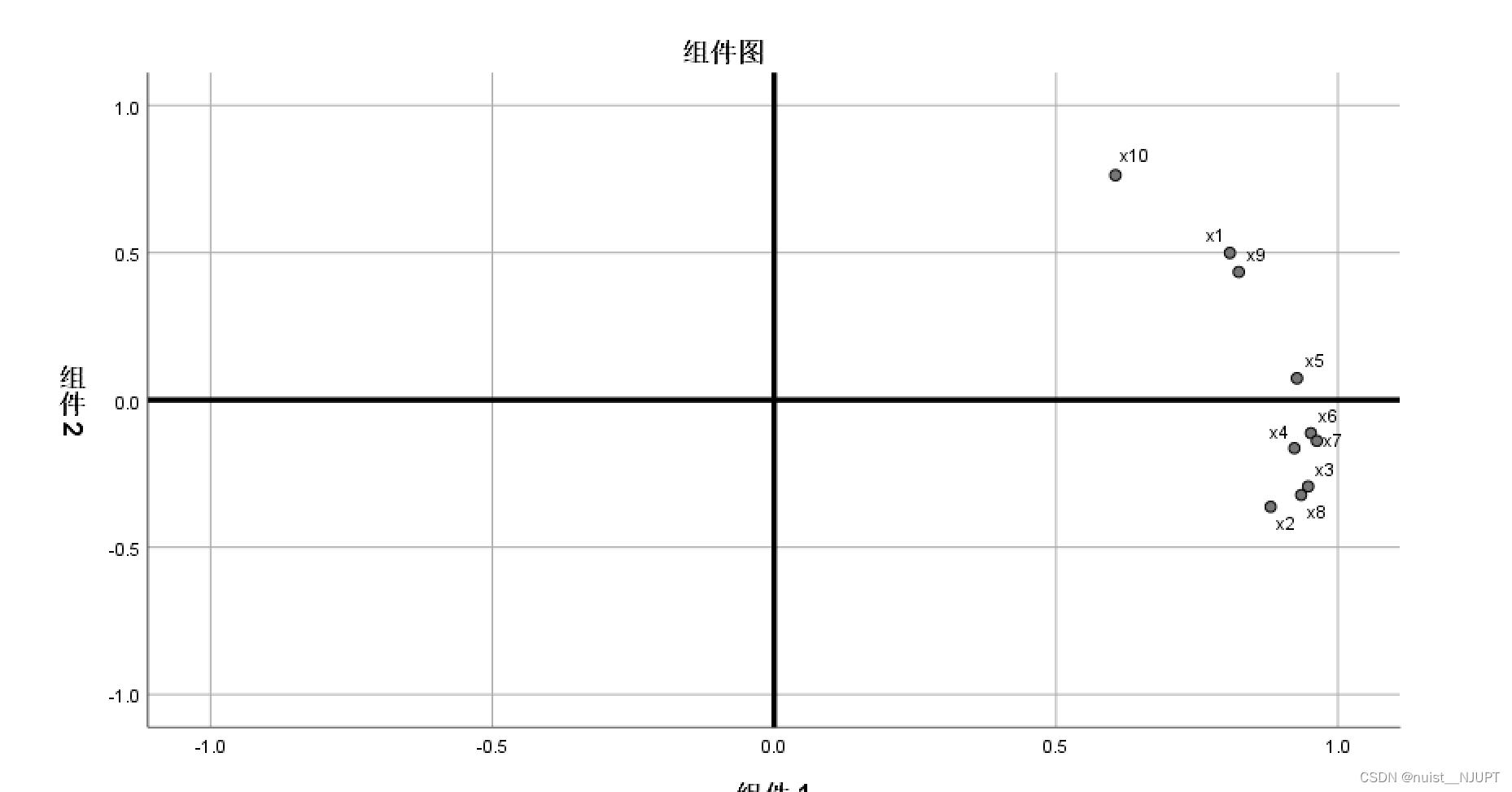
4-成分矩阵和载荷图
从图中可以看到成分的相关性按从大到小排列,相关性差距小的点聚在一起。类似于聚类。
5-计算综合得分
步骤1:将提取出的两个特征值7.791和1.406分别开根号,将成分矩阵的系数分别除以两个开完根号的特征值。这样就得到了每个因素前面的权重,得到主成分表达式y1和y2如下所示。
步骤2:对原始数据进行标准化,将标准化的原始数据带入表达式中,计算各个样本的主成分的得分。
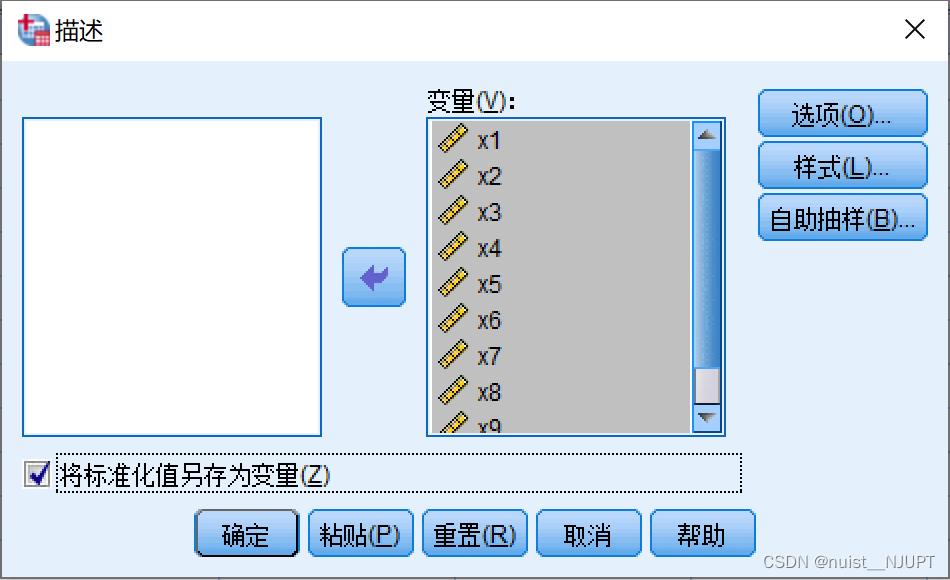
首先是用SPSS标准化原始数据,选择分析->描述统计->描述,将10个变量的标准化值另存为变量即可。如下所示。
得到标准化数据,带入y1和y2的表达式进行计算就可以了,当让用excel算就行
本次提供用SPSS计算的方法,如下:
最后根据主成分y1和y2的占比,计算综合得分。如下所示:
综合得分结果如下:
二、因子分析模型
1-因子分析模型基本原理
因子分析模型室友皮尔曼在1904年首次提出,在某种程度上可以被看成是主成分析的扩展。因子分析法通过研究变量间的相关系数矩阵,把这些变量错综复杂的关系归结成少数几个综合因子,由于归结出的因子的个数少于原始变量的个数,但它又包含了原始变量的信息,所以,这一分析过程也称作降维。由于因子分析比主成分析更易得到解释,故因子分析比主成功分析更容易成功,从而有更广泛的应用。
关于因子分析 ,我们需要知道以下几个概念:
1-因子载荷,比如:a11,a12之类的,相当于回归系数,绝对值越大,说明公共因子与原变量的关系越强。a组成的矩阵称为因子载荷矩阵。
2-变量公共度:就是a11,...a1m的平方和,即所有公共因子对改变量信息的解释程度,如果大部分变量的共同度都高于0.8,则说明该公共因子已经能反应各原始变量80%的信息。
3-方差贡献:因子F对原始变量对所有原始变量总方差的解释能力,其值越高,说明该因子的重要程度越高,是衡量一个公共因子的重要指标。
其中x1...xp代表原始向量,F代表公共因子。最后的参数
代表特殊因子。
2-因子分析法基本步骤
步骤1:选取原始变量,根据原始变量求出相关性系数矩阵,相关性要大于0.3, 巴特利特球形度检验和KMO检验,要求KMO检验值大于等于0.6,越近于1越好, 巴特利特球形度检验显著性值小于0.05,可以拒绝各变量相互独立的假设。
步骤2:提取出特征值大于1,方差贡献率大于80%的因子作为公共因子。
步骤3:旋转,一般常用最大方差法旋转。
步骤4:计算因子变量的得分,一般利用方差贡献率的比例作为权重。
3-因子分析法SPSS实现
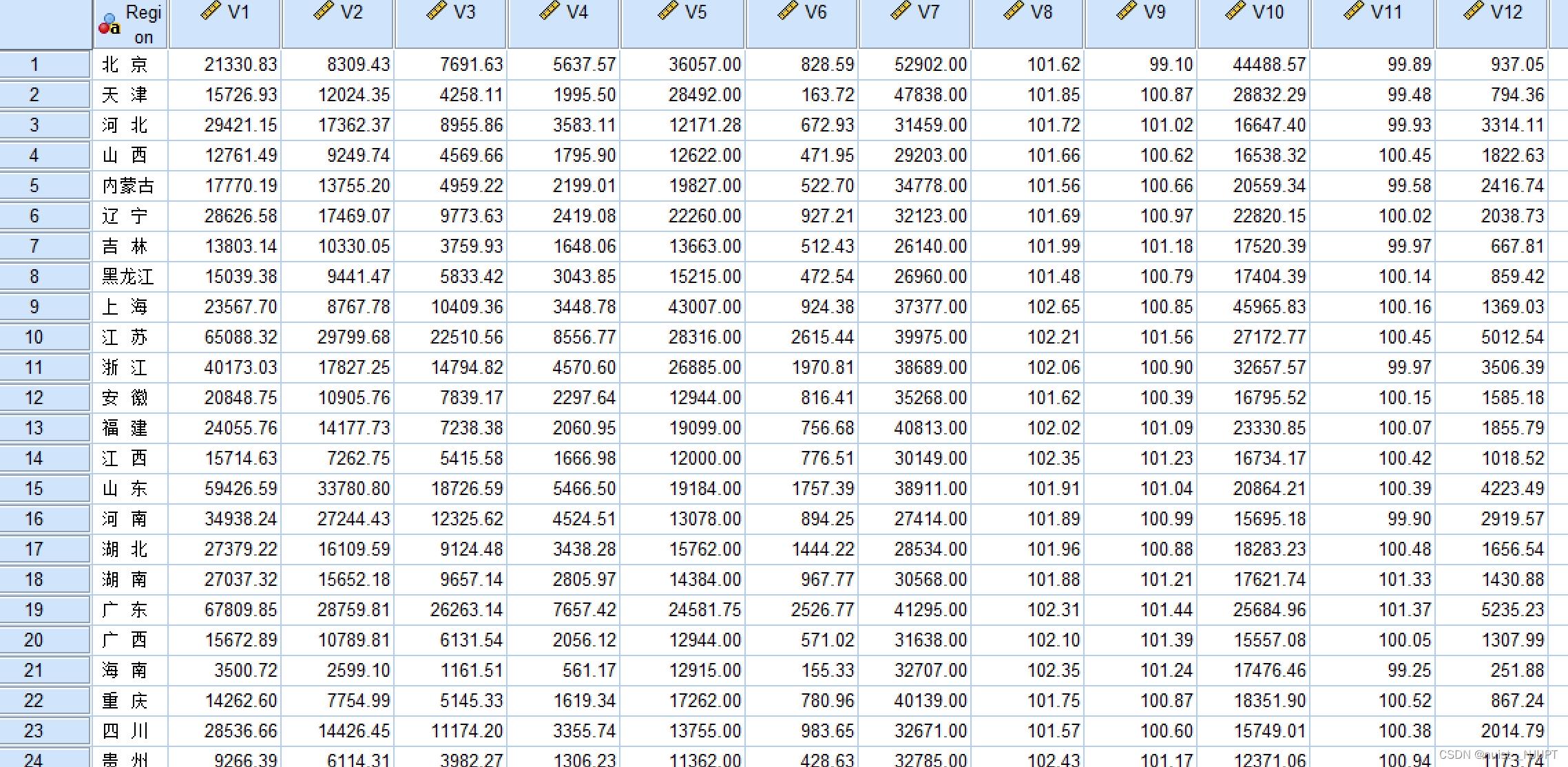
如下图是 各个省份的指标,根据指标使用因子分析降维,计算各个省份的综合得分。
使用SPSS进行因子分析步骤如下:
1-选择分析->降维->因子,然后将12个因子作为变量导入。
2-描述选项勾选KMO和巴特利特球形度检验。
3-提取选项中勾选碎石图。
后面的步骤放到了下面
下面看一下SPSS的分析情况,具体如下:
KMO检验值小于等于0.6,显著性sig小于0.05,拒绝各变量相互独立的假设,各个变量之间具有较强的相关性。
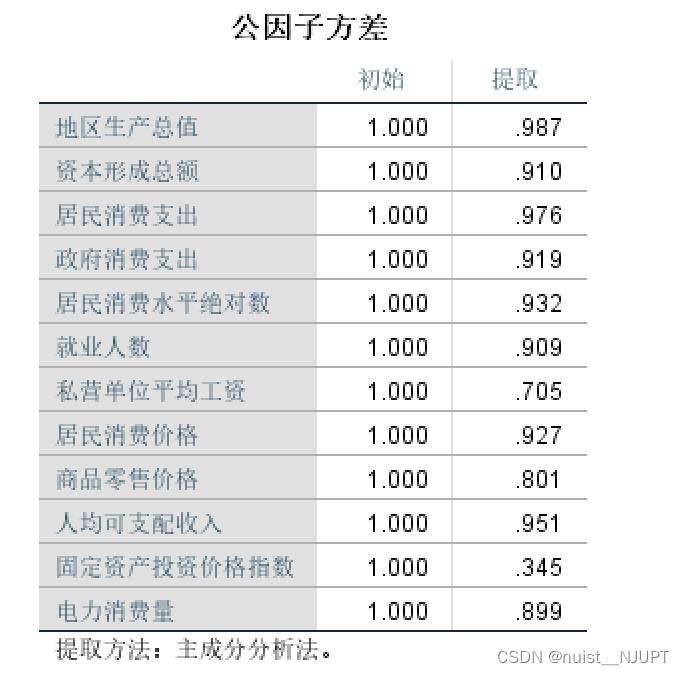
下面看一下公因子方差表,具体如下:
从该表中可以发现:大部分变量的提取比例都在80%以上,提取的公因子对大多数变量的解释能力较强。当然提取的公因子对固定资产投资价格指数的代表性很差,提取的比例只有34.5%.
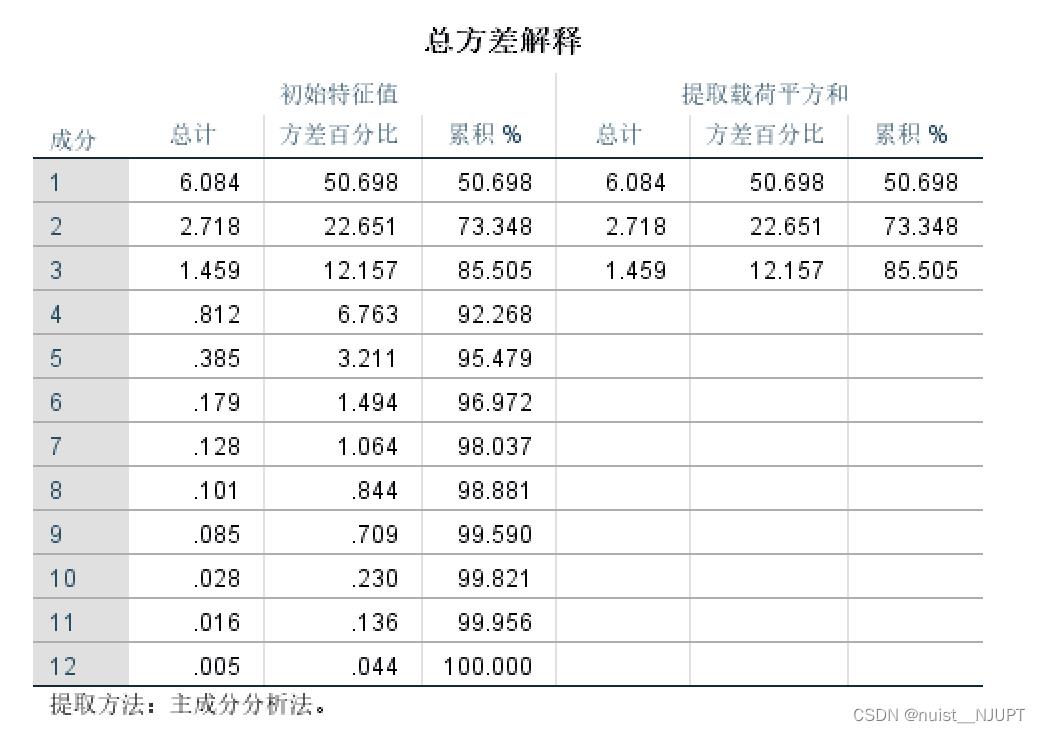
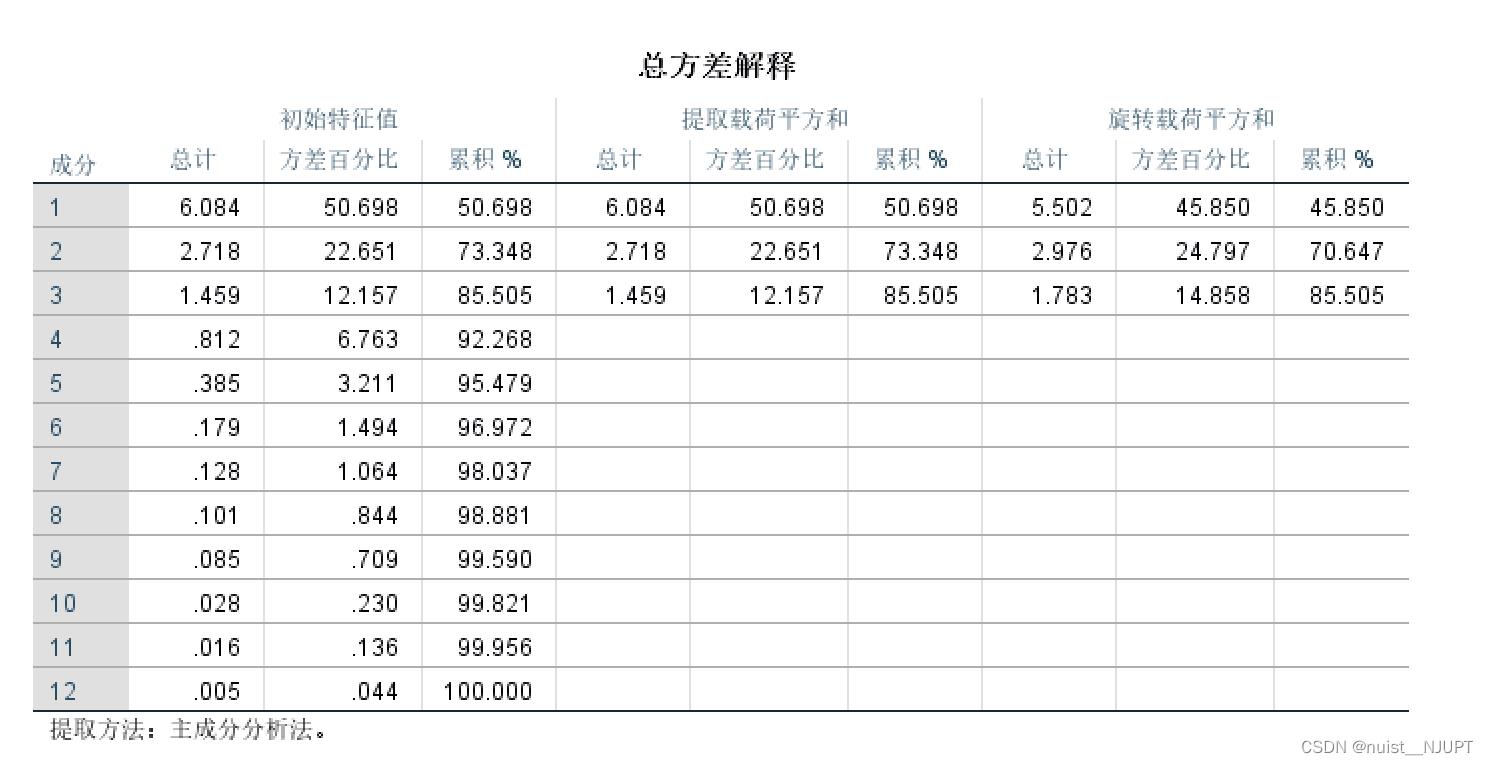
我们看一下总方法解释表,具体如下:
表中给出了各成分的方差贡献率和累积贡献率,前三个主成分的累积贡献率达到了85.5%,可以描述经济发展水平。
我们继续看一下碎石图,具体如下:
我们可以看到前三个因子的三点位于陡坡,特征值大于1,考虑前3个因子即可。
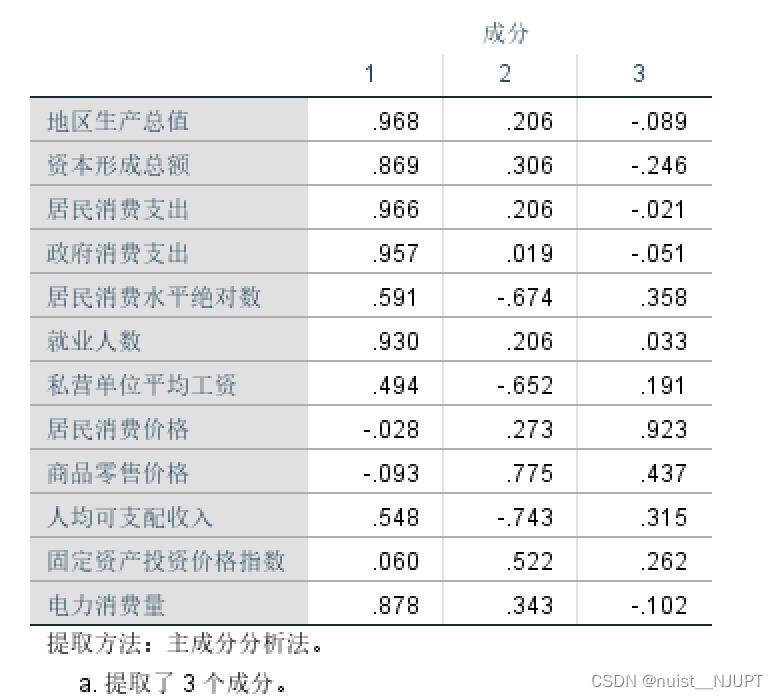
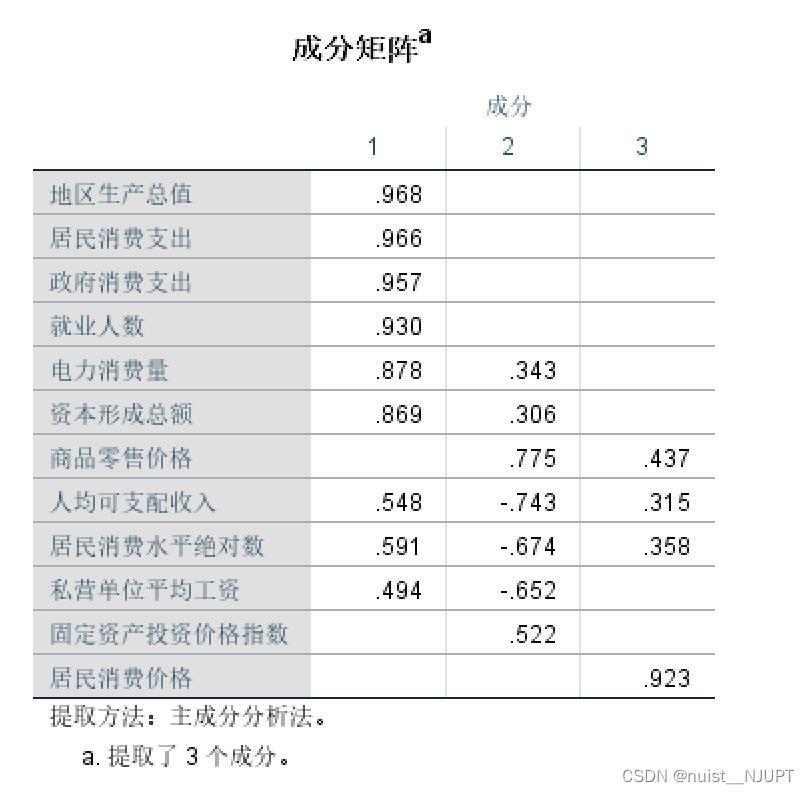
我们继续看一下成分分析表,具体如下:
在因子分析中,按行阅读此表,反应的是各因子在各变量上的载荷,即各因子对各变量的影响度。
因子分析要求提取出的公共因子有实际的含义,为了使因子载荷矩阵中的系数更加显著,对初始因子载荷矩阵进行旋转,将因子和原始变量的关系进行重新分配,从而更加容易进行解释。
4-在旋转选项勾选最大方差法和载荷图。
5-在选项中勾选按大小排序和排除最小系数,排除小系数可以不选择,这边选择设置为0.3.
下面看一下总方差解释表,具体如下所示:
该表最右侧给出了旋转后各因子的载荷情况,旋转会根据提取的3各公共因子所进行,旋转后各个公共子的方差贡献率发生了变化,累积方差贡献率未改变。
下面我们对比一下旋转前后的载荷矩阵,具体如下:
从旋转后的载荷矩阵可以发现,第一个公共因子在地区生产总值、居民消费支出等反应经济状况的指标方面有较大的载荷,故可以命名为:总量因子;第二个公共因子在人均可支配收入等方面具有较大的载荷,因此可以命名为:消费因子;第三个公共因子在居民消费价格等方面具有较大的载荷,因此可以命名为价格因子。与旋转前相比,旋转后各因子的意义更加明确。
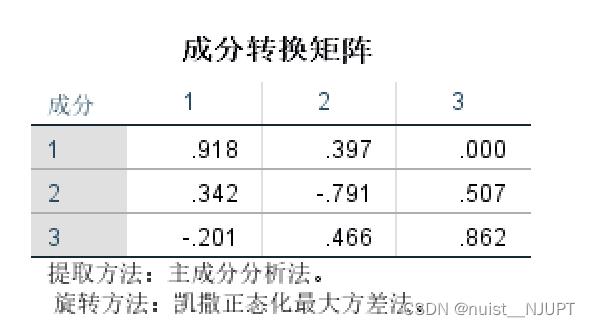
下面看一下成分转换矩阵,具体如下:
成分转换矩阵给出各因子之间的相关系数。
接下来,我们就要写出因子表达式,求出综合得分并进行评价。
6-在SPSS中选择分析->降维->因子->在得分选项勾选保存为变量以及显示因子的得分系数矩阵。
我们看一下得到的得分系数矩阵,具体如下所示:
根据得分系数矩阵,可以直接写出各公共因子的表达式,比如第一个公共因子的表达式如下F1所示:
我们将各因子的得分保存为了新变量,FAC1_1,FAC2_1,FAC3_1。由于三个公共因子分别从不同方面反应经济发展状况,单独使用某个公因子很难全面的评价,因此考虑以各公因子的方差贡献率比例为权重计算综合得分。
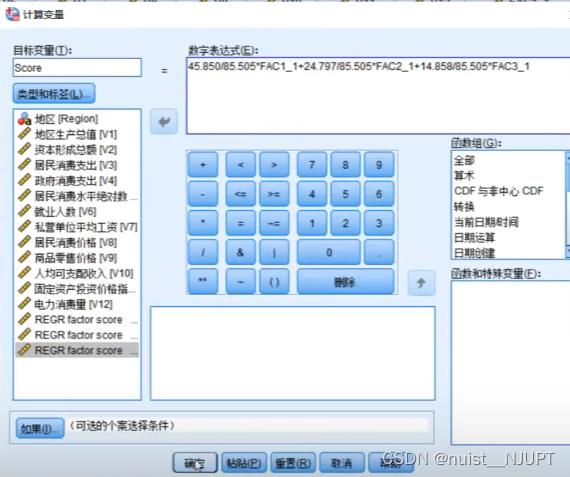
在SPSS中点击转换->计算变量,生成一个新的目标变量Score,通过各个公共因子的方差贡献率比例作为权重计算出来的。如下所示:
上述点击确定,即可生成各个城市的得分情况,可以进行降序排序,最后综合得分排名前几名分别为:广东,江苏,山东,浙江,上海,北京。
需要注意的是:在计算综合的时候,需要注意有没有反向因子,如果有,需要取相反数进行计算。
 创作打卡挑战赛
创作打卡挑战赛
 赢取流量/现金/CSDN周边激励大奖
赢取流量/现金/CSDN周边激励大奖
以上是关于备战数学建模10-主成分分析模型与因子分析模型的主要内容,如果未能解决你的问题,请参考以下文章