备战数学建模33-灰色预测模型2
Posted nuist__NJUPT
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了备战数学建模33-灰色预测模型2相关的知识,希望对你有一定的参考价值。
目录
本节主要学习灰色系统的概念和基本原理,以及介绍了三种灰色预测模型,并给出了灰色预测的具体步骤,同时对比分析了三种灰色预测,针对灰色预测给出了一个经典案例,并给出了MATLAB代码及案例分析,最后对预测类模型和灰色预测模型的适用范围进行了总结分析,下面我们开始好好学习吧!
一、灰色系统的概念
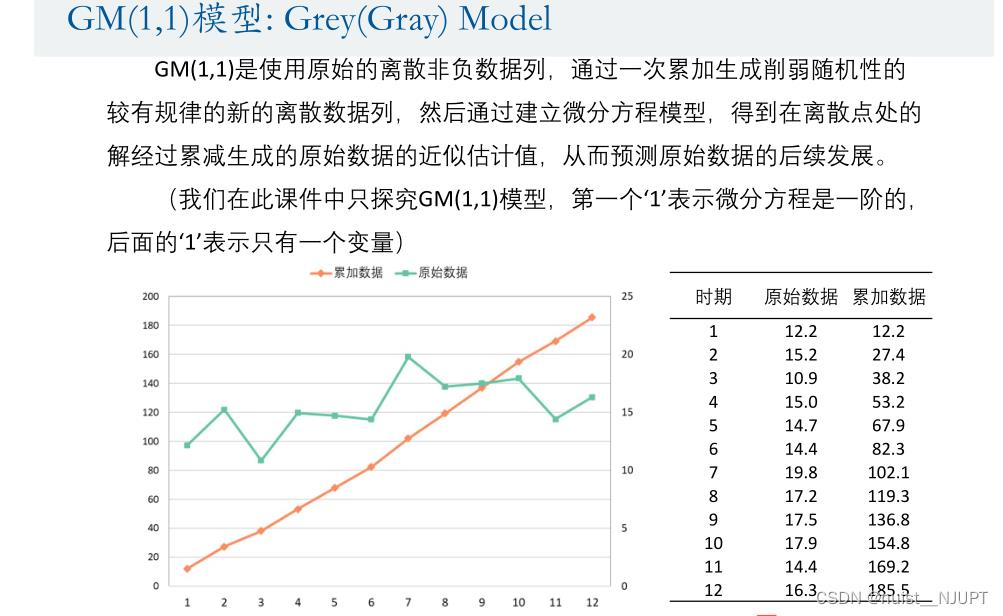
我们看一下灰色系统的概念,就是系统的部分数据已知,部分数据未知,称为灰色系统,而灰色预测则是针对原始数列通过依次累加等方式生成规律的数据序列,然后建立相应的微分方程,进而实现对未来事物的发展趋势进行预测。
GM(1,1)模型适用于 原始离散的非负序列,且最好是年份作为横坐标的且数据大于等于 4期,一般我们只考虑一个变量的一次累加。
二、3种GM(1,1)模型基本原理和实现步骤
进行灰色预测之前需要对数据进行准指数规律检验,也有书上说要进行级比检验,只有检验通过才可以考虑使用 灰色预测,否则,不可以使用灰色预测。
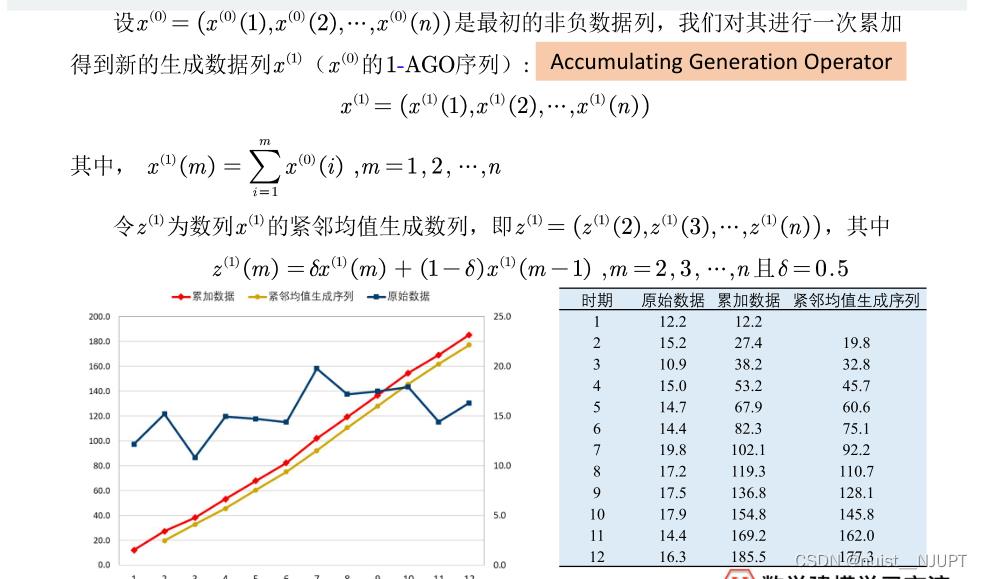
准指数规律检验和级比检验通过之后,我们对原始数据绘制时间序列图观察是否是非负的数列,然后进行一次累加和求紧邻均值生成序列。
接下来我们构造灰色预测模型,并使用最小二乘法进行参数估计,求出参数a和b。
最后,讲灰色方程转换未白化方程,并求解,然后讲数列还原成累加前的原始数列即可进行 预测。
当然,还需要对模型进行残差检验和级偏差检验,只有通过检验才能说明莫模型的预测偏差较小,可以满足预测需求,否则说明灰色预测模型的预测效果不佳。
我们可以使用三种GM对比,将数据分为训练组和测试组,判断那种模型的预测效果好,则使用哪一种,或者直接对三种和模型预测效果取均值。传统GM就是用老数据进行预测,新信息是每次讲预测的信息加入再进行预测,新陈代谢就是每次将老信息剔除然后加入信息进行预测。
三、经典案例
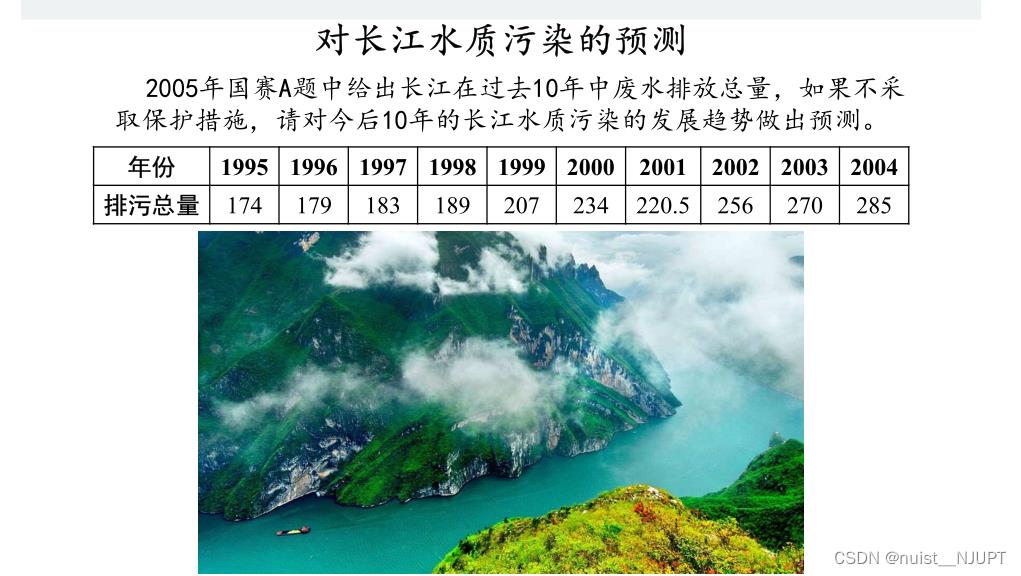
我们看一下这个例题,对于给出长江过去10年的污染情况,预测未来10年的污染情况。
对上述题目进行分析的过程具体如下,首先绘制原始数据的时间序列图,明显是以年份为度量的期数大于4的数据,所以可以考虑灰色预测模型,然后就是准指数规律检验和级比检验,通过检验,才可以使用灰色预测模型,然后由于有10期,前8期分为训练组,后两期为试验组,选择误差平方和SSE最小的灰色预测模型进行预测,最后画出预测后的数据和原来数据的时序图并显示结果,同时需要进行残差检验和级比偏差检验。
MATLAB主函数代码如下:
clear; clc
year = 1995:1:2004; %年份
x0 = [174,179,183,189,207,234,220.5,256,270,285] ;%原始数据序列
n = length(x0);
year = year' ;
x0 = x0' ;
%画出时序图,观察是否是以年份为度量的非负数据
figure(1) ;
plot(year, x0, 'o-') ;
grid on ;
set(gca,'xtick',year(1:1:end)) ; %设置x轴的间隔为1
xlabel('年份'); ylabel('排污总量');
%GM模型适用于数据较短的非负序列,所以要进行非负检验
ERROR = 0; % 建立一个错误指标,一旦出错就指定为1
% 判断是否有负数元素,当然数据量要4~10期才考虑使用GM
if sum(x0<0) > 0
disp('原始数据有负值,不能使用GM')
ERROR = 1;
end
%进行准指数规律检验和进行级比检验
if ERROR == 0
disp('------------------------------------------------------------')
disp('准指数规律检验')
x1 = cumsum(x0); % 一次累加
rho = x0(2:end) ./ x1(1:end-1) ; % 计算光滑度rho(k) = x0(k)/x1(k-1)
% 画出光滑度的图形,并画上0.5的直线,表示临界值
figure(2)
plot(year(2:end),rho,'o-',[year(2),year(end)],[0.5,0.5],'-'); grid on;
text(year(end-1)+0.2,0.55,'临界线') % 在坐标(year(end-1)+0.2,0.55)上添加文本
set(gca,'xtick',year(2:1:end)) % 设置x轴横坐标的间隔为1
xlabel('年份'); ylabel('原始数据的光滑度'); % 给坐标轴加上标签
disp(strcat('指标1:光滑比小于0.5的数据占比为',num2str(100*sum(rho<0.5)/(n-1)),'%'))
disp(strcat('指标2:除去前两个时期外,光滑比小于0.5的数据占比为',num2str(100*sum(rho(3:end)<0.5)/(n-3)),'%'))
disp('参考标准:指标1一般要大于60%, 指标2要大于90%,你认为本例数据可以通过检验吗?')
flag = 1 ;
for k = 2 : n
lamda(k) = x0(k-1) / x0(k) ;
if (lamda(k) < exp(-2 / (n+1)) || lamda(k) > exp(2 / (n+1)))
disp('不通过级比检验!!!') ;
flag = 0 ;
end
end
if flag == 1
disp('通过级比检验!!!') ;
end
%画出级比检验图
figure(3)
x3 = 1: length(lamda)-1 ;
plot(x3, lamda(2:end), 'o-',[x3(1),x3(end)],[exp(2 / (n+1)),exp(2 / (n+1))],[x3(1),x3(end)],[exp(-2 / (n+1)),exp(-2 / (n+1))]) ;
grid on ;
text(2,exp(2 / (n+1)+0.05),'级比上限') ;
text(2,exp(-2 / (n+1)-0.05),'级比下限') ;
set(gca,'xtick',x3(1:1:end)) ;
set(gca,'ytick',0.5:0.1:1.5) ;
axis([1 x3(end) 0.5 1.5]) ;
xlabel('级比个数'); ylabel('级比值');
Judge = input('你认为可以通过准指数规律的检验吗?可以通过请输入1,不能请输入0:');
if Judge == 0
disp('亲,灰色预测模型不适合你的数据哦~ 请考虑其他方法吧 例如ARIMA,指数平滑等')
ERROR = 1;
end
disp('------------------------------------------------------------')
end
%% 当数据量大于4时,我们利用试验组来选择使用传统的GM(1,1)模型、新信息GM(1,1)模型还是新陈代谢GM(1,1)模型; 如果数据量等于4,那么我们直接对三种方法求一个平均来进行预测
if ERROR == 0 && flag == 1 % 如果上述错误均没有发生时,才能执行下面的操作步骤
if n > 4 % 数据量大于4时,将数据分为训练组和试验组(根据原数据量大小n来取,n为5-7个则取最后两年为试验组,n大于7则取最后三年为试验组)
disp('因为原数据的期数大于4,所以我们可以将数据组分为训练组和试验组') % 注意,如果试验组的个数只有1个,那么三种模型的结果完全相同,因此至少要取2个试验组
if n > 7
test_num = 3;
else
test_num = 2;
end
train_x0 = x0(1:end-test_num); % 训练数据
disp('训练数据是: ')
disp(mat2str(train_x0')) % mat2str可以将矩阵或者向量转换为字符串显示, 这里加一撇表示转置,把列向量变成行向量方便观看
test_x0 = x0(end-test_num+1:end); % 试验数据
disp('试验数据是: ')
disp(mat2str(test_x0')) % mat2str可以将矩阵或者向量转换为字符串显示
disp('------------------------------------------------------------')
% 使用三种模型对训练数据进行训练,返回的result就是往后预测test_num期的数据
disp(' ')
disp('***下面是传统的GM(1,1)模型预测的详细过程***')
result1 = gm11(train_x0, test_num); %使用传统的GM(1,1)模型对训练数据,并预测后test_num期的结果
disp(' ')
disp('***下面是进行新信息的GM(1,1)模型预测的详细过程***')
result2 = new_gm11(train_x0, test_num); %使用新信息GM(1,1)模型对训练数据,并预测后test_num期的结果
disp(' ')
disp('***下面是进行新陈代谢的GM(1,1)模型预测的详细过程***')
result3 = metabolism_gm11(train_x0, test_num); %使用新陈代谢GM(1,1)模型对训练数据,并预测后test_num期的结果
% 现在比较三种模型对于试验数据的预测结果
disp(' ')
disp('------------------------------------------------------------')
% 绘制对试验数据进行预测的图形(对于部分数据,可能三条直线预测的结果非常接近)
test_year = year(end-test_num+1:end); % 试验组对应的年份
figure(4);
plot(test_year,test_x0,'o-',test_year,result1,'*-',test_year,result2,'+-',test_year,result3,'x-'); grid on;
set(gca,'xtick',year(end-test_num+1): 1 :year(end)) % 设置x轴横坐标的间隔为1
legend('试验组的真实数据','传统GM(1,1)预测结果','新信息GM(1,1)预测结果','新陈代谢GM(1,1)预测结果') % 注意:如果lengend挡着了图形中的直线,那么lengend的位置可以自己手动拖动
xlabel('年份'); ylabel('排污总量'); % 给坐标轴加上标签
% 计算误差平方和SSE
SSE1 = sum((test_x0-result1).^2);
SSE2 = sum((test_x0-result2).^2);
SSE3 = sum((test_x0-result3).^2);
disp(strcat('传统GM(1,1)对于试验组预测的误差平方和为',num2str(SSE1)))
disp(strcat('新信息GM(1,1)对于试验组预测的误差平方和为',num2str(SSE2)))
disp(strcat('新陈代谢GM(1,1)对于试验组预测的误差平方和为',num2str(SSE3)))
if SSE1<SSE2
if SSE1<SSE3
choose = 1; % SSE1最小,选择传统GM(1,1)模型
else
choose = 3; % SSE3最小,选择新陈代谢GM(1,1)模型
end
elseif SSE2<SSE3
choose = 2; % SSE2最小,选择新信息GM(1,1)模型
else
choose = 3; % SSE3最小,选择新陈代谢GM(1,1)模型
end
Model = '传统GM(1,1)模型','新信息GM(1,1)模型','新陈代谢GM(1,1)模型';
disp(strcat('因为',Model(choose),'的误差平方和最小,所以我们应该选择其进行预测'))
disp('------------------------------------------------------------')
% 选用误差最小的那个模型进行预测
predict_num = input('请输入你要往后面预测的期数: ');
% 计算使用传统GM模型的结果,用来得到另外的返回变量:x0_hat, 相对残差relative_residuals和级比偏差eta
[result, x0_hat, relative_residuals, eta] = gm11(x0, predict_num); % 先利用gm11函数得到对原数据拟合的详细结果
% % 判断我们选择的是哪个模型,如果是2或3,则更新刚刚由模型1计算出来的预测结果
if choose == 2
result = new_gm11(x0, predict_num);
end
if choose == 3
result = metabolism_gm11(x0, predict_num);
end
% 输出使用最佳的模型预测出来的结果
disp('------------------------------------------------------------')
disp('对原始数据的拟合结果:')
for i = 1:n
disp(strcat(num2str(year(i)), ' : ',num2str(x0_hat(i))))
end
disp(strcat('往后预测',num2str(predict_num),'期的得到的结果:'))
for i = 1:predict_num
disp(strcat(num2str(year(end)+i), ' : ',num2str(result(i))))
end
% 如果只有四期数据,那么我们就没必要选择何种模型进行预测,直接对三种模型预测的结果求一个平均值~
else
disp('因为数据只有4期,因此我们直接将三种方法的结果求平均即可~')
predict_num = input('请输入你要往后面预测的期数: ');
disp(' ')
disp('***下面是传统的GM(1,1)模型预测的详细过程***')
[result1, x0_hat, relative_residuals, eta] = gm11(x0, predict_num);
disp(' ')
disp('***下面是进行新信息的GM(1,1)模型预测的详细过程***')
result2 = new_gm11(x0, predict_num);
disp(' ')
disp('***下面是进行新陈代谢的GM(1,1)模型预测的详细过程***')
result3 = metabolism_gm11(x0, predict_num);
result = (result1+result2+result3)/3;
disp('对原始数据的拟合结果:')
for i = 1:n
disp(strcat(num2str(year(i)), ' : ',num2str(x0_hat(i))))
end
disp(strcat('传统GM(1,1)往后预测',num2str(predict_num),'期的得到的结果:'))
for i = 1:predict_num
disp(strcat(num2str(year(end)+i), ' : ',num2str(result1(i))))
end
disp(strcat('新信息GM(1,1)往后预测',num2str(predict_num),'期的得到的结果:'))
for i = 1:predict_num
disp(strcat(num2str(year(end)+i), ' : ',num2str(result2(i))))
end
disp(strcat('新陈代谢GM(1,1)往后预测',num2str(predict_num),'期的得到的结果:'))
for i = 1:predict_num
disp(strcat(num2str(year(end)+i), ' : ',num2str(result3(i))))
end
disp(strcat('三种方法求平均得到的往后预测',num2str(predict_num),'期的得到的结果:'))
for i = 1:predict_num
disp(strcat(num2str(year(end)+i), ' : ',num2str(result(i))))
end
end
% 绘制相对残差和级比偏差的图形(注意:因为是对原始数据的拟合效果评估,所以三个模型都是一样的哦~~~)
figure(5)
subplot(2,1,1) % 绘制子图(将图分块)
plot(year(2:end), relative_residuals,'*-'); grid on; % 原数据中的各时期和相对残差
legend('相对残差'); xlabel('年份');
set(gca,'xtick',year(2:1:end)) % 设置x轴横坐标的间隔为1
subplot(2,1,2)
plot(year(2:end), eta,'o-'); grid on; % 原数据中的各时期和级比偏差
legend('级比偏差'); xlabel('年份');
set(gca,'xtick',year(2:1:end)) % 设置x轴横坐标的间隔为1
disp(' ')
disp('****下面将输出对原数据拟合的评价结果***')
%% 残差检验
average_relative_residuals = mean(relative_residuals); % 计算平均相对残差 mean函数用来均值
disp(strcat('平均相对残差为',num2str(average_relative_residuals)))
if average_relative_residuals<0.1
disp('残差检验的结果表明:该模型对原数据的拟合程度非常不错')
elseif average_relative_residuals<0.2
disp('残差检验的结果表明:该模型对原数据的拟合程度达到一般要求')
else
disp('残差检验的结果表明:该模型对原数据的拟合程度不太好,建议使用其他模型预测')
end
% 级比偏差检验
average_eta = mean(eta); % 计算平均级比偏差
disp(strcat('平均级比偏差为',num2str(average_eta)))
if average_eta<0.1
disp('级比偏差检验的结果表明:该模型对原数据的拟合程度非常不错')
elseif average_eta<0.2
disp('级比偏差检验的结果表明:该模型对原数据的拟合程度达到一般要求')
else
disp('级比偏差检验的结果表明:该模型对原数据的拟合程度不太好,建议使用其他模型预测')
end
disp(' ')
disp('------------------------------------------------------------')
% 绘制最终的预测效果图
figure(6) % 下面绘图中的符号m:洋红色 b:蓝色
plot(year,x0,'-o', year,x0_hat,'-*m', year(end)+1:year(end)+predict_num,result,'-*b' ); grid on;
hold on;
plot([year(end),year(end)+1],[x0(end),result(1)],'-*b')
legend('原始数据','拟合数据','预测数据') % 注意:如果lengend挡着了图形中的直线,那么lengend的位置可以自己手动拖动
set(gca,'xtick',[year(1):1:year(end)+predict_num]) % 设置x轴横坐标的间隔为1
xlabel('年份'); ylabel('排污总量'); % 给坐标轴加上标签
end
传统GM(1,1)模型函数代码如下:
function [result, x0_hat, relative_residuals, eta] = gm11(x0, predict_num)
% 函数作用:使用传统的GM(1,1)模型对数据进行预测
% x0:要预测的原始数据
% predict_num: 向后预测的期数
% 输出变量 (注意,实际调用时该函数时不一定输出全部结果,就像corrcoef函数一样~,可以只输出相关系数矩阵,也可以附带输出p值矩阵)
% result:预测值
% x0_hat:对原始数据的拟合值
% relative_residuals: 对模型进行评价时计算得到的相对残差
% eta: 对模型进行评价时计算得到的级比偏差
n = length(x0); % 数据的长度
x1=cumsum(x0); % 计算一次累加值
z1 = (x1(1:end-1) + x1(2:end)) / 2; % 计算紧邻均值生成数列(长度为n-1)
% 将从第二项开始的x0当成y,z1当成x,来进行一元回归 y = kx +b
y = x0(2:end); x = z1;
% 下面的表达式就是第四讲拟合里面的哦~ 但是要注意,此时的样本数应该是n-1,少了一项哦
k = ((n-1)*sum(x.*y)-sum(x)*sum(y))/((n-1)*sum(x.*x)-sum(x)*sum(x));
b = (sum(x.*x)*sum(y)-sum(x)*sum(x.*y))/((n-1)*sum(x.*x)-sum(x)*sum(x));
a = -k; %注意:k = -a哦
% 注意: -a就是发展系数, b就是灰作用量
disp('现在进行GM(1,1)预测的原始数据是: ')
disp(mat2str(x0')) % mat2str可以将矩阵或者向量转换为字符串显示
disp(strcat('最小二乘法拟合得到的发展系数为',num2str(-a),',灰作用量是',num2str(b)))
disp('***************分割线***************')
x0_hat=zeros(n,1); x0_hat(1)=x0(1); % x0_hat向量用来存储对x0序列的拟合值,这里先进行初始化
for m = 1: n-1
x0_hat(m+1) = (1-exp(a))*(x0(1)-b/a)*exp(-a*m);
end
result = zeros(predict_num,1); % 初始化用来保存预测值的向量
for i = 1: predict_num
result(i) = (1-exp(a))*(x0(1)-b/a)*exp(-a*(n+i-1)); % 带入公式直接计算
end
% 计算绝对残差和相对残差
absolute_residuals = x0(2:end) - x0_hat(2:end); % 从第二项开始计算绝对残差,因为第一项是相同的
relative_residuals = abs(absolute_residuals) ./ x0(2:end); % 计算相对残差,注意分子要加绝对值,而且要使用点除
% 计算级比和级比偏差
class_ratio = x0(2:end) ./ x0(1:end-1) ; % 计算级比 sigma(k) = x0(k)/x0(k-1)
eta = abs(1-(1-0.5*a)/(1+0.5*a)*(1./class_ratio)); % 计算级比偏差
end新信息GM(1,1)模型函数代码:
function [result] = new_gm11(x0, predict_num)
% 函数作用:使用新信息的GM(1,1)模型对数据进行预测
% 输入变量
% x0:要预测的原始数据
% predict_num: 向后预测的期数
% 输出变量
% result:预测值
result = zeros(predict_num,1); % 初始化用来保存预测值的向量
for i = 1 : predict_num
result(i) = gm11(x0, 1); % 将预测一期的结果保存到result中
x0 = [x0; result(i)]; % 更新x0向量,此时x0多了新的预测信息
end
end
新陈代谢GM(1,1)模型函数代码:
function [result] = metabolism_gm11(x0, predict_num)
% 函数作用:使用新陈代谢的GM(1,1)模型对数据进行预测
% 输入变量
% x0:要预测的原始数据
% predict_num: 向后预测的期数
% 输出变量
% result:预测值
result = zeros(predict_num,1); % 初始化用来保存预测值的向量
for i = 1 : predict_num
result(i) = gm11(x0, 1); % 将预测一期的结果保存到result中
x0 = [x0(2:end); result(i)]; % 更新x0向量,此时x0多了新的预测信息,并且删除了最开始的那个向量
end
end运行结果分析:
如下是原始数据时序图,以年份为度量的非负数据。

下面的图2和图3是准指数规律检验和级比检验。显然都通过了。


图4试验组三个模型的预测结果与实际的真实数据的偏差程度示意图,可以发现新陈代谢模型效果更好,更接近真实值,误差平方和较小。
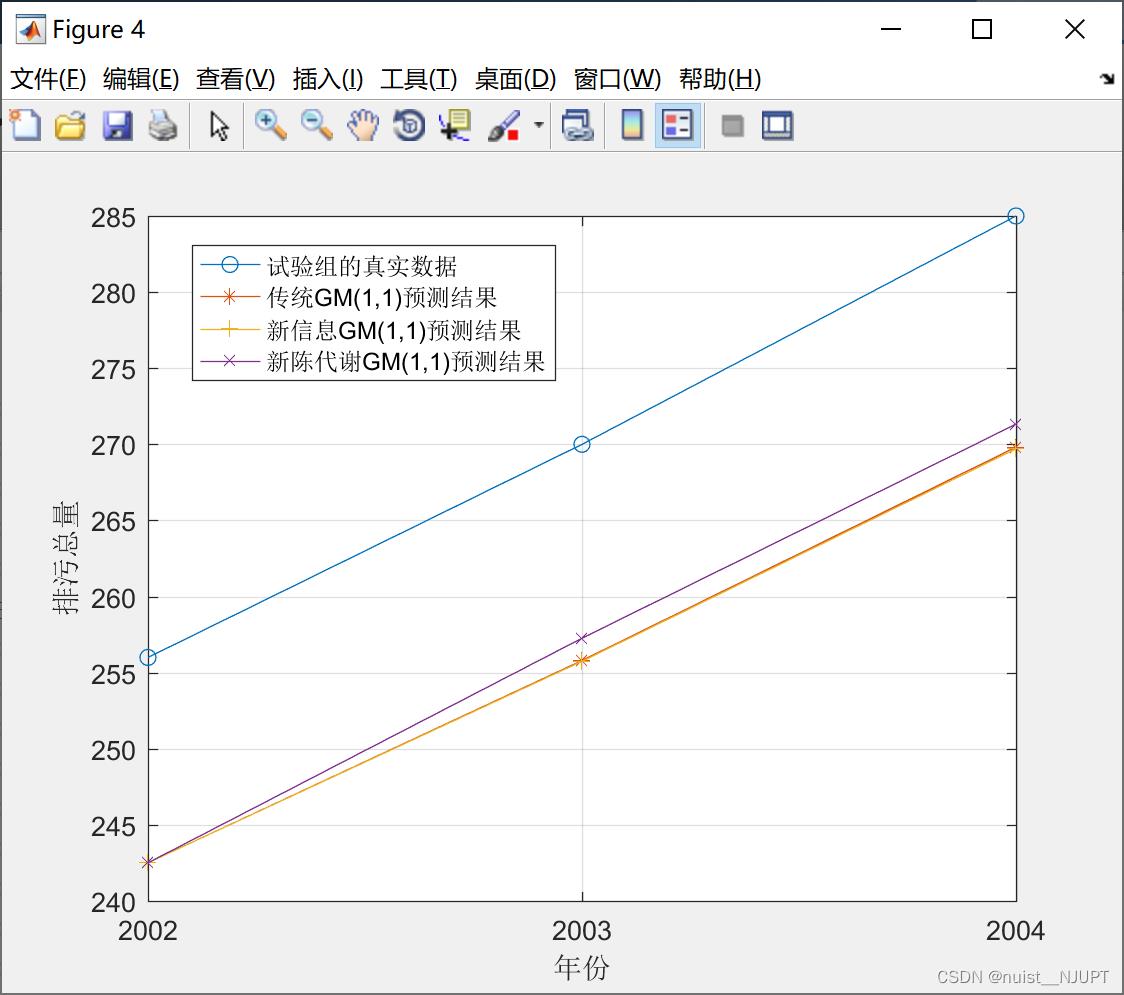
下面的图5是残差检验和级比偏差检验。可以发现基本都小于0.1,全部小于0.2。检验通过。

最后的是未来10年污染情况预测结果图,分别给出绅士数,拟合曲线,以及灰色模型预测的曲线,可以发现预测的效果还是不错的。
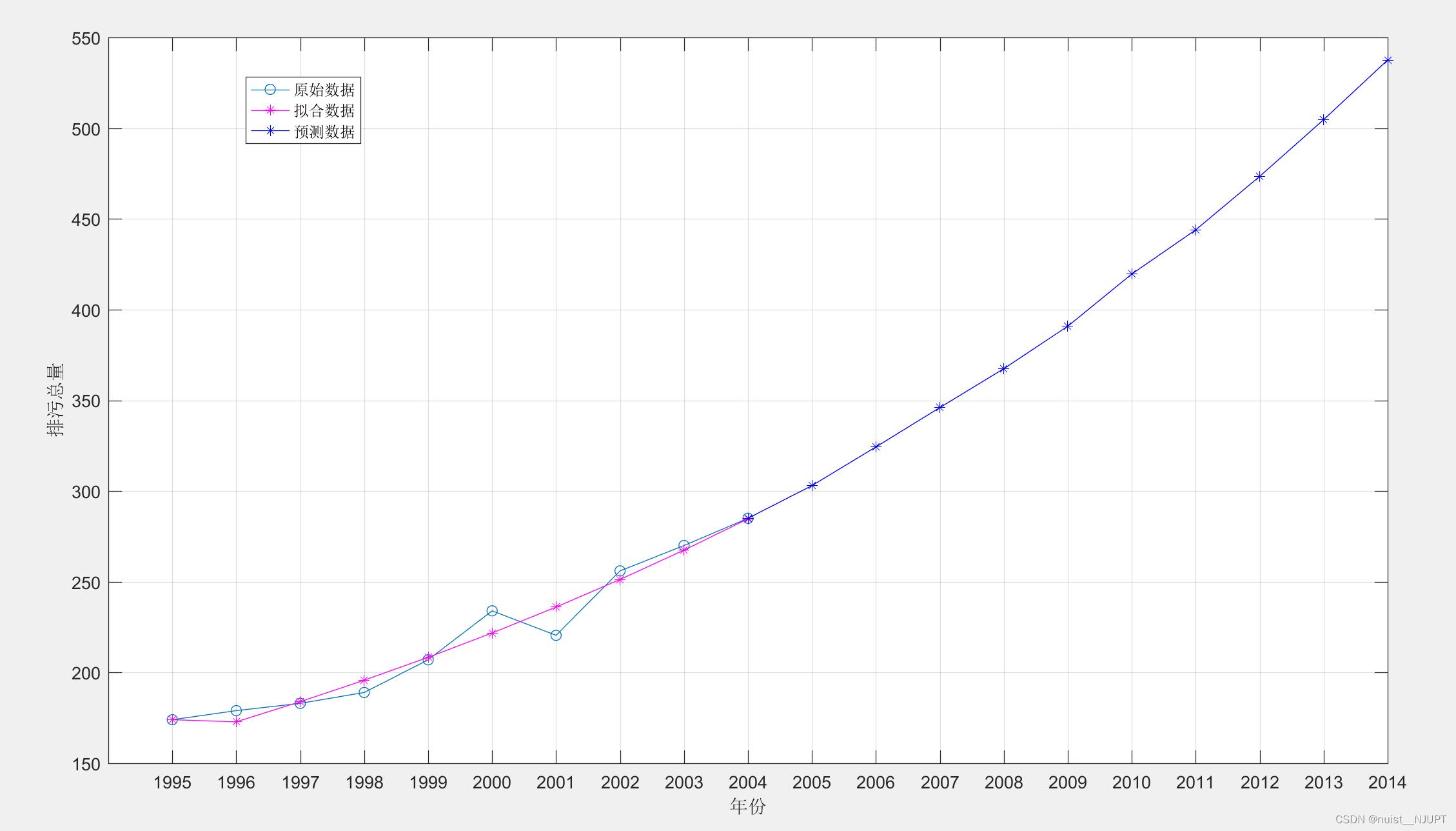
四、总结分析
对于预测类题目,我们可以根据如下步骤确定我们所需要的模型,先画图分析,然后数分组尝试不同模型,选择模型进行预测,最后画出预测后的数据和原来数据的时序图,看看预测趋势是否合理。
对于什么时候,我们使用灰色预测模型呢,主要考虑下面三点,即原始数据是以年份度量的非负数据,数据能够通过预检验,数据的期数最好事4~10期的。
以上是关于备战数学建模33-灰色预测模型2的主要内容,如果未能解决你的问题,请参考以下文章