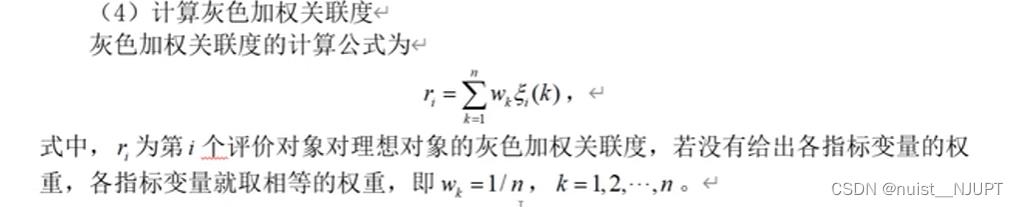备战数学建模24-灰色关联分析2

Posted 2022-05-20 nuist__NJUPT

目录

一、灰色关联分析

1-基本概念及步骤

2-经典案例及MATLAB编程实现

---

一、灰色关联分析

1-基本概念及步骤

灰色关系分析：就是计算某一个待比较的数列和参照数列的关联程度，关联程度越高，说明待比较数列越接近关联数列，则待比较数列越好。

我们看一下灰色关联分析的基本步骤：

第一步：我们需要确定比较数列和参考数列，参考数列就是最好的值。对于效益性指标就是最大值。当然需要对数据进行归一化处理，所有指标转换成极大型，消除量纲的影响。

 第二步：我们需要确定各个指标的权重，当然可以省略，直接等权重即可。

 第三步：计算灰色关联系数，具体公式如下：

第四步：计算灰色加权联度，具体如下：

 第五步：评价分析，根据灰色关联度大小进行排序，灰色关联度越大越好，越大则说明和参照数列越接近。

2-经典案例及MATLAB编程实现

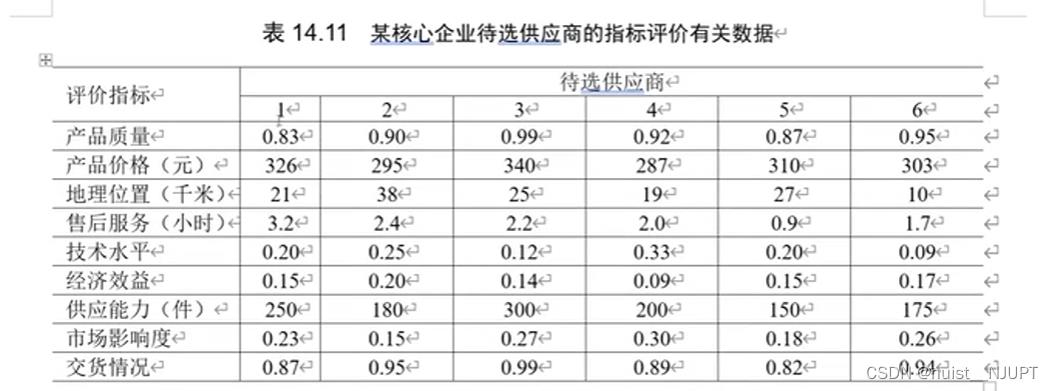
我们看个例子，关于供应商选择决策问题，某个企业需要在6个零件供应商中选择一个合作伙伴，各供应商数据如下所示：

下表中供应商6个，评价指标9个，2，3，4是成本型指标，其余是效益性指标 ；

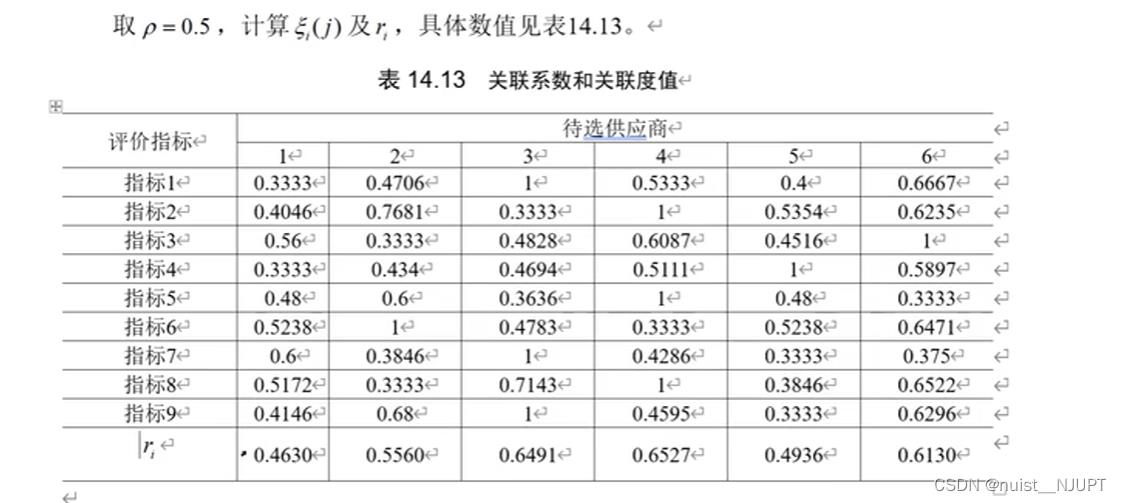
使用灰色关联度分析算法，计算出的关联度系数和灰色关联度如下表：

上述灰色关联度分析的MATLAB代码如下所示：

clear; clc
a = [0.83, 0.9, 0.99, 0.92, 0.87, 0.95;
     326, 295, 340, 287, 310, 303;
     21, 38, 25, 19, 27, 10;
     3.2, 2.4, 2.2, 2, 0.9, 1.7;
     0.2, 0.25, 0.12, 0.33, 0.2, 0.09;
     0.15, 0.20, 0.14, 0.09, 0.15,0.17;
     250, 180, 300, 200, 150, 175;
     0.23, 0.15, 0.27, 0.3, 0.18, 0.26;
     0.87, 0.95, 0.99, 0.89, 0.82, 0.94] ;
 [n,m] = size(a) ;
 for i = [1 5:9] %对效益型指标标准化处理
     a(i,:) = (a(i,:) - min(a(i,:))) / (max(a(i,:)) - min(a(i,:))) ;
 end
 for i = 2 : 4 %对成本型指标进行标准化处理
     a(i,:) = (max(a(i,:)) - a(i,:)) / (max(a(i,:)) - min(a(i,:))) ;
 end

ck = max(a,[],2) ; %逐行求最大值，得到列向量，即参考数列

for i = 1 : n 
    for j = 1 : m 
        x1(i,j) = abs(a(i,j) - ck(i,1)) ; %求出参考数列
    end
end

mmin = min(min(x1)) ;
mmax = max(max(x1)) ;

 rho = 0.5 ; %分辨系数
 x = (mmin + rho * mmax) ./ (x1 + rho * mmax) ; %计算灰色关联度系数
 g = mean(x) ; %计算关联度，取等权重
 [gsort, index] = sort(g, 'descend') ; %对关联度进行由大到小排序
 disp('关联度排名如下：') ;
 disp(index) ;

总结一下：灰色关联度分析，用于比较待比较的数列和参照数列的关联程度，用于对各项指标进行综合评价，具体步骤如下：

1）确定比较数列和参考数列；

2）对参考数列和比较数列进行无量纲化处理；

3）定各个指标的权重；(可以省略)

4）计算灰色关联系数；

5）计算灰色加权关联度；

6）根据灰色加权关联度进行排序，综合评价；