备战数学建模36-时间序列模型2

Posted 2022-07-01 nuist__NJUPT

目录

一、ARCH和GARCH模型基本介绍

二、经典案例分析

---

本节主要介绍ARCH模型和GARCH模型（拓展/广义的ARCH模型），ARCH模型全称“自回归条件异方差模型”，在现代高频金融时间序列中，数据经常出现波动性聚集的特点，但从长期来看数据是平稳的，即长期方差无条件方差）是定值，但从短期来看方差是不稳定的，我们称这种异方差为条件异方差。传统的时间序列模型如ARMA模型识别不出来这一特征。ARCH模型由美国加州大学恩格尔(Engle)教授1982年在《计量经济学》杂志（Econometrica）的一篇论文中首次提出，此后在计量经济领域中得到迅速发展，恩格尔教授也于2003年获诺贝尔经济学奖。

一、ARCH和GARCH模型基本介绍

有了ARIMA等时间序列模型，为什么要引入GARCH模型呢，因为对于呈现波动性聚集的数据，长期看平稳，短期看不平稳，即存在条件异方差，这种情况下，传统的时间序列模型往往识别不出来，因此引出了ARCH模型和GARCH模型。

我们看一下条件异方差的概念，短期看，存在异方差，我们称为条件异方差，在ARMA模型的基础之上提出了ARCH模型，一般考虑的ARCH模型均是乘法条件异方差。

 我们看一下ARCH(1)模型和ARCH(q)模型，时间序列具有ARCH(1)效应和时间序列具有ARCH(q)效应，从实际定义上，很容易发现ARCH模型本质上就是对t进行建模。

 我们再看一下GARCH(p,q)模型，在ARCH模型基础之上进行了扩展，得到了GARCH模型，我们可以看到加入了ht的约束。

我们看一下检验GARCH效应的方法，需要进行白噪声检验，若是白噪声，则不存在GARCH效应，则不能使用GARCH模型进行预测，反之，存在GARCH效应，可以使用GARCH模型进行预测。当然还有一种LM检验用于检验是否具有GARCH效应，具体后面会介绍。

我们需要知道什么时候使用ARCH模型和GARCH模型呢， 其实就是扰动项存在异方差的时候，一般初步可以通过绘制时序图来观察，看数据是否存在波动性据集。

一般来说，严格的统计检验方法有三种：

方法1：LM检验，方法2：Q检验，方法3：系数显著性检验。

二、经典案例分析

我们看一个股票收益率预测的案例，分别建立了ARMA模型和GARCH模型进行预测。

首先使用原始数据绘制时间序列图，可以明显看出序列是不平稳的，特别是2015年到2016年的变动很剧烈。

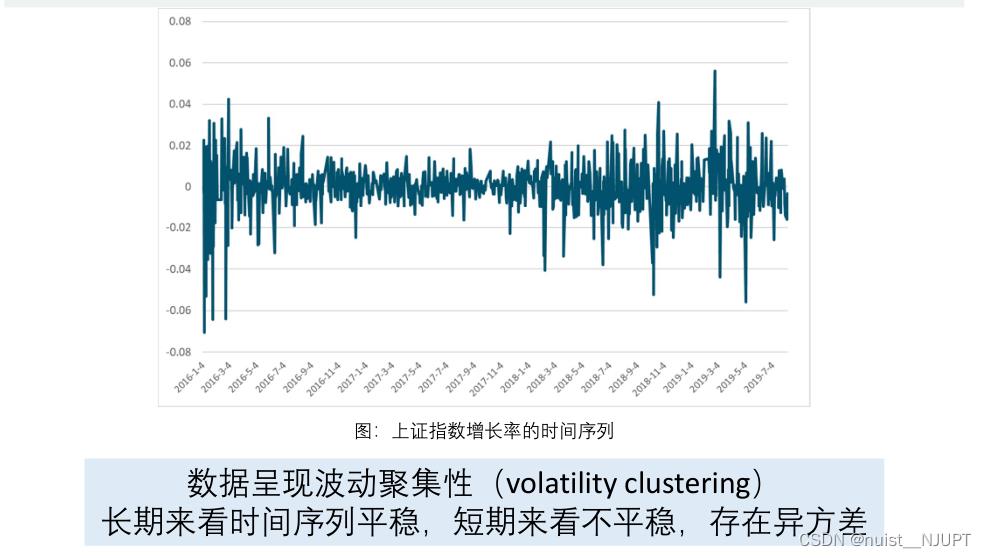
我们需要计算日收益率，对日收益率进行描述统计，同时做出日收益率的时间序列图，具体如下所示，可以发现日收益率在0值附近波动，当值最好收益率5.86,最低收益率-8.68，均值还是在0附近。

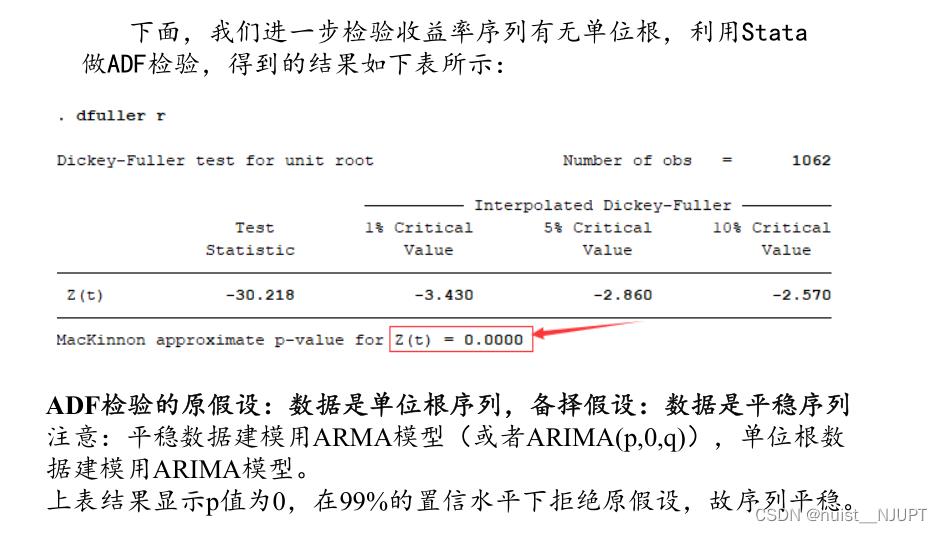
下面我们需要检验收益率序列r是否为单位根,检验方法是ADF检验(原假设：是单位根序列，备择假设：是平稳序列)，可以发现p值小于0.05，拒绝原假设，认为序列平稳，则可以选择ARMA模型进行预测。

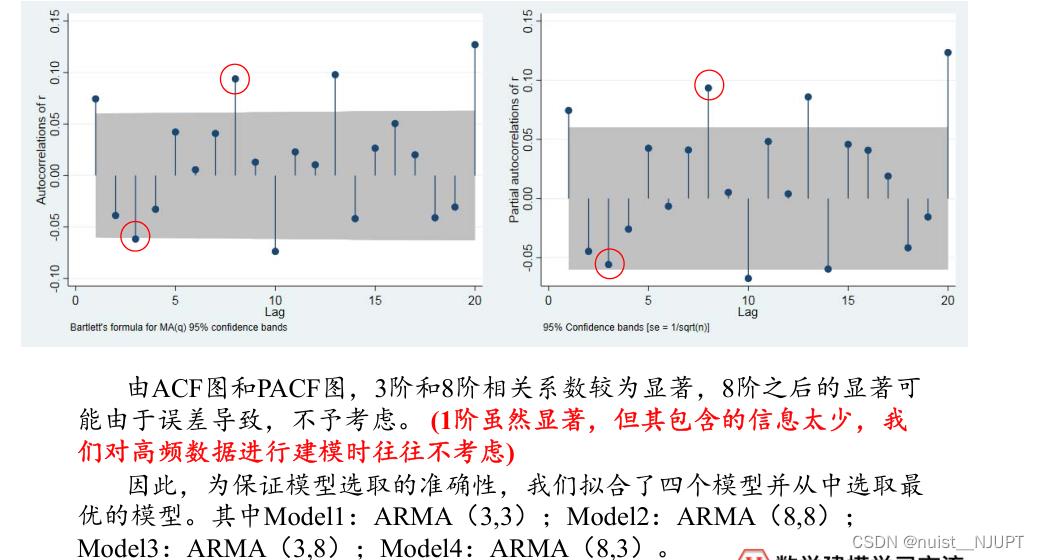
我们使用stata绘制相关系数ACF和偏相关系数PACF图，从图中可以发现3阶和8阶的相关系数较为显著，那么考虑的p和q就是3和8的组合，可以选取四种ARMA模型。

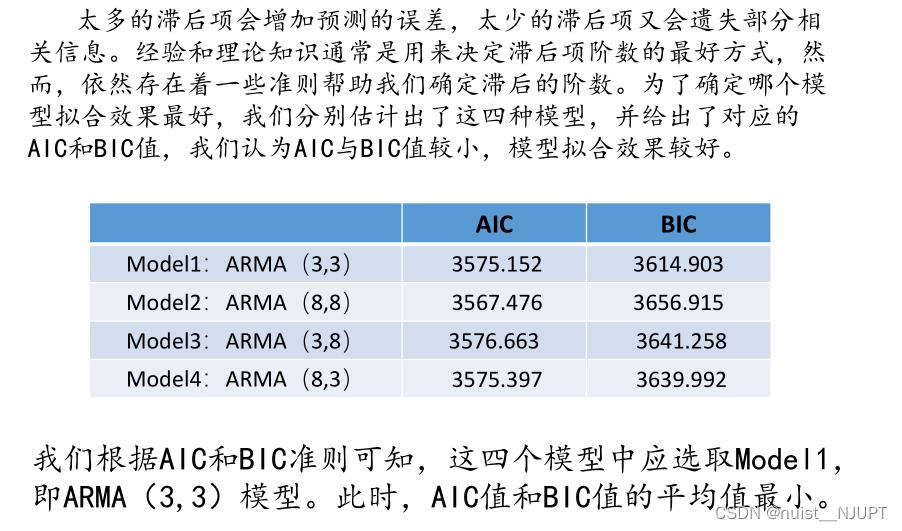
对于上述的四个ARMA模型，我们事应AIC和BIC值去比较模型的拟合效果，AIC和BIC的值越小，则说明模型的拟合效果越好，明显model1的AIC和BIC均值最小，选择model1.

下面对ARMA(3,3)模型进行参数估计，得到的参数值如下所示。

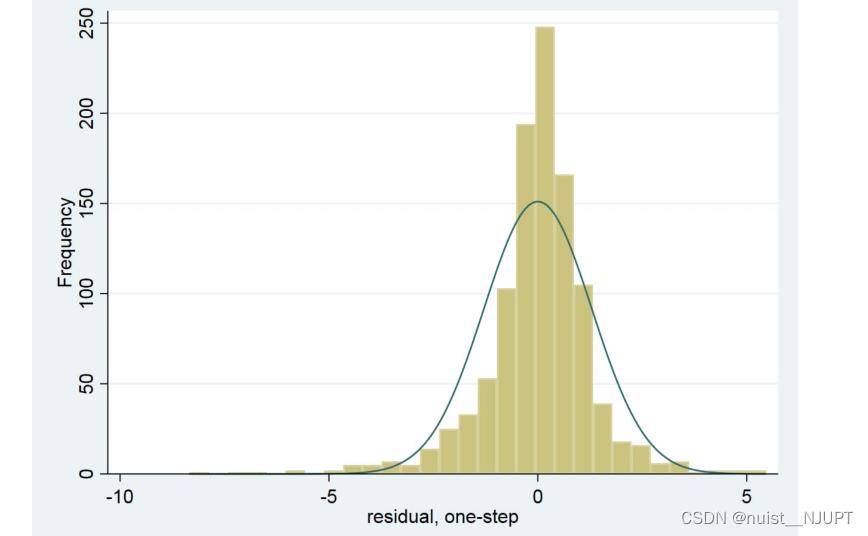
我们得到残差的预测值并生成残差分布直方图，如下所示。

我们需要检验残差是否是白噪声，P值大于0.05,不能拒绝原假设，残差是白噪声，残差不存在明显的相关性，故认为模型的有效性较好。

因为还需要使用GARCH模型，所以我们需要进行LM检验：检验是否存在GARCH误差，即存在GARCH效应，存在GARCH效应，才可以考虑使用GARCH模型，否则不可以使用。LM统计量是显著异于0的，故认为存在ARCH误差。

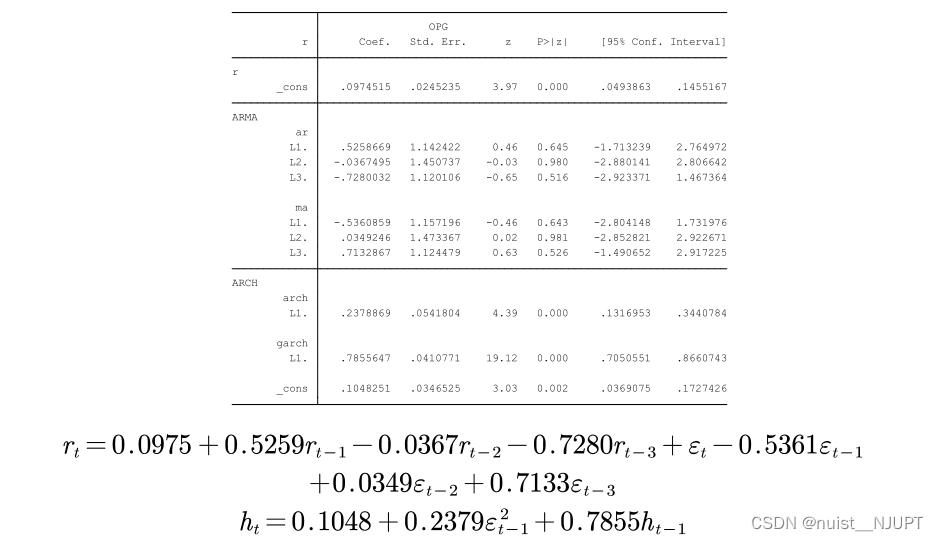
利用AIC和BIX值，选择合适的GARCH模型，我们选择的是是GARCH(1,1)模型，具体如下所示，t分布下扰动项的ARMA(3,3)进行估计。

我们需要对GARCH模型进行参数估计， 具体的参数估计值如下所示。

最后，将时间数据延长10期，就可以对数据进行预测了，具体的预测结果如下，可以发现只能预测前四期，后面就保持不变了。

上述预测的stata代码如下所示：

clear  // 清空变量
* (1) 导入数据并生成时间序列  (*和//都可以用来注释一行)
insheet using "Bindex.csv"  //导入位于和代码同一文件夹下的csv数据文件
gen datevar = date(date,"YMD")   // 将csv中的变量date转换为stata能识别的时间数据datevar
format datevar %td // 对datevar的展示格式进行转换，转换后以:日月年 显示
label variable datevar "日期"  // 设置datevar的标签为日期，主要用于画图时的展示
tsset datevar   // 定义datevar是一个时间序列数据
gen time=_n  // 定义一个从1到n的time序列，n是观测值的个数，系统自动在后台记录的
tsset time   // 将time这个序列定义为时间序列，后续滞后算子时需要用到


// 画深成B指的时间序列图
line index datevar   
graph export "深成B指的时间序列图.png", as(png) replace   // 导出图片到本地文件夹

// 计算日收益率数据
gen r=100*(index-L.index)/L.index   //（今天的收盘价-昨天的收盘价）/昨天的收盘价   L是lag的缩写

// 对日收益率r进行描述性统计
summarize r  

// 做出日收益率的时间序列图
line r datevar
graph export "深成B指日收益率的时间序列图.png", as(png) replace   // 导出图片到本地文件夹


// 检验收益率序列r是否为单位根,检验方法是ADF检验(原假设：是单位根序列，备择假设：是平稳序列)
dfuller r
// MacKinnon approximate p-value for Z(t) = 0.0000  p值为0意味着拒绝原假设，所以我们认为r序列平稳


// 观察acf图与pacf图 ，判断AMRA模型的阶数
ac r,lags(20)   // 自相关系数图，滞后20期
graph export "自相关系数图.png", as(png) replace   // 导出图片到本地文件夹

pac r,lags(20)  // 偏自相关系数图，滞后20期
graph export "偏自相关系数图.png", as(png) replace   // 导出图片到本地文件夹


// 根据acf和pacf图，初步判断使用四个备选的ARMA模型来拟合
set matsize 1500  // 把计算时支持的最大矩阵大小设置的大一点，否则计算机性能较差的电脑可能在计算中会报错
arima r,arima(3,0,3)   // 用ARIMA(3,0,3)模型对r进行估计
estat ic   // 得到AIC和BIC，用于选择合适的模型（选小原则，详见第十一讲）
arima r,arima(8,0,8)
estat ic
arima r,arima(3,0,8)
estat ic
arima r,arima(8,0,3)
estat ic


// ARIMA(3,0,3)模型的AIC值和BIC值的平均值最小，所以下面我们使用这个模型进行估计 
arima r,arima(3,0,3)

// 得到残差的预测值并生成残差分布直方图图
predict residess, residuals   // 保存残差
hist residess,norm freq  // norm freq表示加上标准正态分布的概率密度函数
graph export "残差分布直方图.png", as(png) replace   // 导出图片到本地文件夹


// 检验残差是否为白噪声序列，检验方法为Q检验：原假设是白噪声，备择假设不是白噪声
wntestq residess, lag(12)   // 对残差序列进行白噪声检验

// 生成残差的平方，并进行Q检验
gen ressq = residess^2   // 生成残差平方序列ressq
wntestq ressq, lag(12) // 对残差平方序列ressq进行白噪声检验

// LM检验：是否存在ARCH误差
reg ressq l.ressq l2.ressq l3.ressq l4.ressq l5.ressq  // 将残差平方项对其滞后项回归
gen LM_STAT=e(N)*e(r2) // 计算LM统计量
display LM_STAT  // 输出LM统计量
display chiprob(e(df_m),LM_STAT) // 计算p值


// 利用AIC BIC选择合适的模型进行估计 
// 注意：扰动项的分布在金融数据中常服从t分布
// 正态分布下GARCH(1,1)估计
arch r,arima(3 0 3) arch(1) garch(1)
estat ic
// t分布下GARCH(1,1)估计
arch r,arima(3 0 3) arch(1) garch(1) distribution(t 3)  // 自由度为3的t分布
estat ic
// 正态分布下GARCH(2,2)估计
arch r,arima(3 0 3) arch(2) garch(2)
estat ic
// t分布下GARCH(2,2)估计
arch r,arima(3 0 3) arch(2) garch(2) distribution(t 3)
estat ic


// 得到拟合结果，并进行预测
arch r,arima(3 0 3) arch(1) garch(1) distribution(t 3)
tsappend ,add(10)  // 将时间延长10期
predict result // 对数据进行预测
tsline result r, legend(label(1 "预测值")  label(2 "真实值"))   // 绘制拟合图
graph export "预测结果图.png", as(png) replace   // 导出图片到本地文件夹