机器学习：线性模型学习总结：线性回归

Posted 2022-04-20 新四石路打卤面

基于周志华老师的《机器学习》、上一篇学习笔记以及网络的其他资料，对线性模型的这一部分内容进行一个总结。

学习时间：2022.04.17~2022.04.18

文章目录

• • 0. 数据预处理
  • 1. 用SK-Learn做线性回归模型
  • • 1.1 线性回归
    • 1.2 随机梯度下降执行线性回归
    • 1.3 多项式回归
    • 1.4 逻辑回归
  • 2. 用SK-Learn评价回归模型
  • • 2.1 回归模型的评价指标
    • 2.2 交叉验证的评价指标
    • 2.3 过拟合与欠拟合
  • 3. 用Sklearn进行网格搜索
  • 4. 完整代码

0. 数据预处理

尝试构建了一个可以通用处理的数据预处理函数（不能处理文本和时间数据，因为要具体情况具体分析）。

    column_lists = list(df)  # 获取所有的列名
    bool_cos = []  # 获取所有的布尔类型列
    classify_cos = []  # 获取所有的分类数据列
    number_cos = []  # 获取所有的数据类型列
    date_cos = []  # 获取所有的时间类型列

    for i in column_lists:
        if df[i].dtypes == 'bool':
            bool_cos.append(i)
        elif df[i].dtypes == 'object':
            classify_cos.append(i)
        elif str(df[i].dtypes) == 'datetime':
            date_cos.append(i)
        else:
            number_cos.append(i)

    # 缺失值添加是否缺失的特征列
    for i in column_lists:
        if df[i].isnull().any():  # 判断是否有缺失值
            # 或者用if np.any(df[i].isnull()):
            new_column = str(i + '_ifNaN')  # 设置新列名
            df[new_column] = df.apply(lambda df: 1 if df[i] == np.NaN else 0, axis=1) 

    # 对于分类型数据，使用众数填充
    for i in classify_cos:
        df[i] = df[i].fillna(df[i].mode()[0])

    # 对于数值型数据，使用均值填充，并进行标准化（归一化的应用场景有限，可能会将数据的间距缩小）
    for i in number_cos:
        df[i].fillna(df[i].mean(), inplace=True)

        def stand_sca(data):
            data_standard = (data-data.mean())/data.std()
            return data_standard

        df[i] = stand_sca(df[i])

    # 对于bool类型数据，使用众数填充，并转换成0和1
    for i in bool_cos:
        df[i].fillna(df[i].mode(), inplace=True)
        df[i] = df[i].astype('int')

    df = pd.get_dummies(df)

1. 用SK-Learn做线性回归模型

1.1 线性回归

sklearn.linear_model.LinearRegression

1.2 随机梯度下降执行线性回归

sklearn.linear_model.SGDRegressor

可能需要调整的参数：

• loss损失函数：要使用的损失函数。

  • loss=“squared_error”：平方误差损失函数，普通最小二乘；
  • “loss=huber”：增强平方误差损失函数对离群点的鲁棒性；
  • “loss=epsilon_insensitive”：标准SVR的损失函数，是L1损耗；
  • “loss=squared_epsilon_insensitive”：epsilon_insensitive的平方，是L2损耗。

• penalty正则化方法：默认为“$l2$”。

  • 有’$l2$’， ‘$l1$’， '$elasticnet$'三种，分别对应岭回归、Lasso回归、弹性回归。

• alpha：使正则化项相乘的常量，值越高，正则化越强（仅针对’$l2$’， ‘$l1$’）。默认值为 0.0001。

• l1_ratio：弹性回归参数，[0,1]。确定’$l2$'和 '$l1$'的比率r，仅当是“弹性网”时才使用。默认0.15。

• max_iter最大迭代次数：默认=1000。

• tol停止的容差标准：如果不是None，则在连续的epoch (loss > best_loss - tol)时停止训练。默认=1e-3。

• epsilon敏感阈值：仅当为’ huber ‘、’ epsilon_insensitive ‘或’ squared_epsilon_insensitive '时。它决定了一个阈值，如果当前预测和正确标签之间的任何差异小于此阈值，则忽略它们。默认为0.1。

• learning_rate：学习率模式：默认default=‘invsscaleing’。

  • ‘constant’: 常量。eta = eta0
  • ‘optimal'：最优。eta = 1.0 / (alpha * (t + t0))
  • ‘invscaling’：内扩。eta = eta0 / pow(t, power_t)
    • power_t默认=0.1。
  • ‘adaptive’：自适应。eta = eta0，但每次连续的 epoch 无法按tol减少训练损失或未能按 tol 提高验证分数 early_stopping时，当前学习速率除以 5。

• eta0初始学习率。默认eta0=0.01。

• early_stopping：当验证分数没有提高时，是否使用提前停止来终止训练。默认值 = False。

  • validation_fraction：要留出的训练数据的比例，用于早期停止的验证集。默认值 = 0.1。

创建模板：

from sklearn.linear_model import SGDRegressor
# 实例化模型
SGDRegressor = SGDRegressor(loss='squared_error', penalty='l2', alpha=0.0001, max_iter=1000, tol=1e-3, eta0=0.01)
# 训练模型
SGDRegressor.fit(train_x, train_y)
# 模型预测
train_result = SGDRegressor.predict(train_x)

1.3 多项式回归

sklearn.preprocessing.PolynomialFeatures

可能需要调整的参数：

• degree：如果给定一个整数，它指定多项式特征的最大度。如果传递了一个元组(min_degree, max_degree)，则min_degree是生成的特征的最小多项式度，max_degree是最大多项式度。注意min_degree=0和min_degree=1是等价的，因为输出的0度项是由include_bias决定的。默认default=2。

在使用PolynomialFeatures()函数后，再使用线性回归，即是多项式回归，PolynomialFeatures()只是一个数据预处理过程。

import numpy as np
from sklearn.preprocessing import PolynomialFeatures
X = np.arange(6).reshape(3, 2)
print(X)
'''
array([[0, 1],
       [2, 3],
       [4, 5]])
'''
poly = PolynomialFeatures(2)
print(poly.fit_transform(X))
'''
array([[ 1.,  0.,  1.,  0.,  0.,  1.],
       [ 1.,  2.,  3.,  4.,  6.,  9.],
       [ 1.,  4.,  5., 16., 20., 25.]])
'''
poly = PolynomialFeatures(interaction_only=True)
print(poly.fit_transform(X))
'''
array([[ 1.,  0.,  1.,  0.],
       [ 1.,  2.,  3.,  6.],
       [ 1.,  4.,  5., 20.]])
'''

1.4 逻辑回归

用于分类：sklearn.linear_model.LogisticRegression

• penalty正则化方法：默认为“$l2$”。
  • 有’$l2$’， ‘$l1$’， '$elasticnet$'三种，分别对应岭回归、Lasso回归、弹性回归。
• l1_ratio：弹性回归参数，[0,1]。确定’$l2$'和 '$l1$'的比率r，仅当是“弹性网”时才使用。默认=None。
• tol停止的容差标准：如果不是None，则在连续的epoch (loss > best_loss - tol)时停止训练。默认=1e-4。
• C正则强度的倒数：与支持向量机一样，较小的值指定更强的正则化。default=1.0。
• solver：用于优化问题的算法。‘newton-cg’, ‘lbfgs’, ‘liblinear’, ‘sag’, ‘saga’, 默认=’lbfgs’。
  • ‘newton-cg’：也是牛顿法家族的一种，利用损失函数二阶导数矩阵即海森矩阵来迭代优化损失函数。
  • ‘lbfgs’：拟牛顿法的一种，利用损失函数二阶导数矩阵即海森矩阵来迭代优化损失函数。
  • ‘liblinear’：不支持设置 penalty='none'；L1正则化，多用于二分类。
  • ‘sag’：要求数据进行缩放处理。支持L2正则化。随机平均梯度下降，是梯度下降法的变种。
  • ⭐‘saga’：要求数据进行缩放处理。支持L1、L2和弹性正则化。
• max_iter：最大迭代次数，默认=100。
• multi_class：分类法类型，默认default=’auto’。
  • ‘auto’：自动判断。
  • ‘ovr’：每个标签都看做二分类问题。
  • ‘multinomial’：Softmax算法，多分类，即使数据是二分类的，损失最小是多项式损失拟合整个概率分布。（当solver =‘liblinear’ 时， ‘multinomial’ 不可用）。

可见：机器学习：线性模型学习总结（2）。

2. 用SK-Learn评价回归模型

2.1 回归模型的评价指标

没有交叉验证的评价指标输出函数：

	MSE = mean_squared_error(true_value, pred_value)
    print("均方误差MSE：", MSE, end=';\\t')

    RMSE = np.sqrt(mean_squared_error(true_value, pred_value))
    print("均方根误差RMSE：", RMSE, end=';\\t')

    MAE = mean_absolute_error(true_value, pred_value)
    print("平均绝对误差MAE：", MAE, end=';\\t')

    R2 = r2_score(true_value, pred_value)
    print("决定系数R-Square：", R2, end=';\\t')

    MAPE = mean_absolute_percentage_error(true_value, pred_value)
    print("平均绝对百分比误差MAPE：", MAPE, end=';\\t')

    EVS = explained_variance_score(true_value, pred_value)
    print("可解释方差：", EVS, end='。')

2.2 交叉验证的评价指标

sklearn.model_selection.cross_val_score

需要定义的参数：

• estimator：需要使用交叉验证的算法，即传入自己定义的模型。

• X：传入数据集。

• y：传入标签。

• scoring：选择评价指标。回归模型默认R2，分类模型默认accuracy。default=None。

  • 其他支持的评分指标如下：

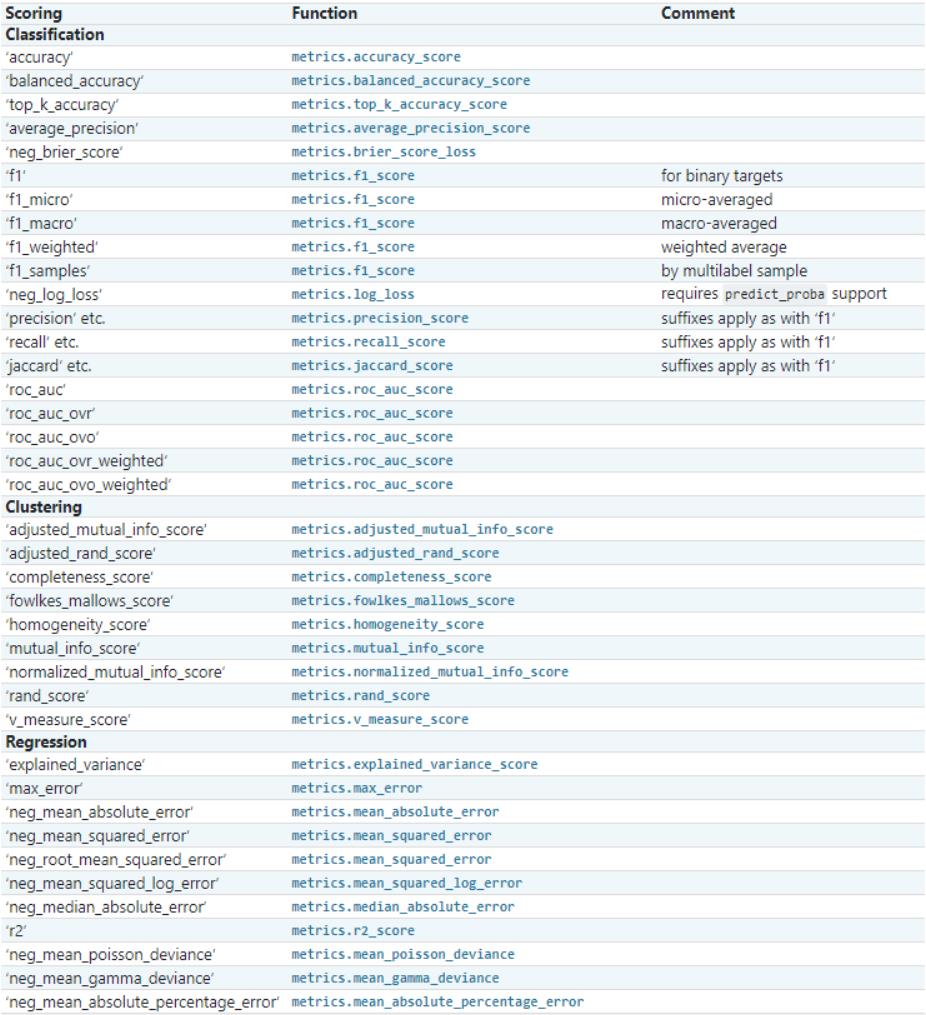
• cv：交叉验证折数或可迭代的次数。default=None。

  • None：使用默认的5倍交叉验证；
  • int：指定(Stratified)KFold中的折叠次数；
  • An iterable that generates (train, test) splits as arrays of indices.

• n_jobs：同时工作的cpu个数（-1代表全部）。default=None。

• pre_dispatch：控制并行执行期间调度的作业数量。减少这个数量对于避免在CPU发送更多作业时CPU内存消耗的扩大是有用的。default=’2*n_jobs’。该参数可以是：

  • None：在这种情况下，所有的工作立即创建并产生。将其用于轻量级和快速运行的作业，以避免由于按需产生作业而导致延迟；
  • An int：一个int，给出所产生的总工作的确切数量；
  • A str：给出一个表达式作为n_jobs的函数，如’2 * n_jobs。

    # 计算交叉验证的MSE
    MSE = cross_val_score(model, test_x, test_y, scoring='neg_mean_squared_error', cv=10)
    print('均方误差MSE：', -MSE)

    # 计算交叉验证的RMSE
    RMSE = np.mean(np.sqrt(np.abs(MSE)))

    # 计算交叉验证的R2
    R2 = cross_val_score(model, test_x, test_y, scoring='r2', cv=10)
    print("决定系数R-Square：", R2)

    print('平均MSE：', np.mean(MSE), ";  平均RMSE：", RMSE, ";  平均R2：", np.mean(R2))

2.3 过拟合与欠拟合

如果模型在训练数据上表现良好，但根据交叉验证的指标泛化较差，则你的模型过拟合。

• 在神经网络模型中，可使用权值衰减的方法，即每次迭代过程中以某个小因子降低每个权值。
• 选取合适的停止训练标准，使对机器的训练在合适的程度；
• 保留验证数据集，对训练成果进行验证；
• 获取额外数据进行交叉验证；
• 正则化，即在进行目标函数或代价函数优化时，在目标函数或代价函数后面加上一个正则项，一般有L1正则与L2正则等。

如果两者的表现均不理想，则说明欠拟合。

• 增加新特征，可以考虑加入进特征组合、高次特征，来增大假设空间；
• 添加多项式特征，这个在机器学习算法里面用的很普遍，例如将线性模型通过添加二次项或者三次项使模型泛化能力更强；
• 减少正则化参数，正则化的目的是用来防止过拟合的，但是模型出现了欠拟合，则需要减少正则化参数；
• 使用非线性模型，比如核SVM 、决策树、深度学习等模型；
• 调整模型的容量(capacity)，通俗地，模型的容量是指其拟合各种函数的能力；
• 容量低的模型可能很难拟合训练集；使用集成学习方法，如Bagging ,将多个弱学习器Bagging。

3. 用Sklearn进行网格搜索

sklearn.model_selection.GridSearchCV

可能需要的参数：

• estimator：参数针对的搜索对象，即要调参的模型。
• param_grid：超参的集合，本质上是一个列表，每个元素代表一组搜索（是一个字典），每个字典中的key是本次一次性要搜索的超参名字，对应的value是一个列表，描述搜索范围，其每个元素是相应的搜索取值。
• scoring：用于评估测试集上交叉验证模型性能的策略。可接受的评价指标可见上图。一个指标即传入字符串；多个指标传入列表。默认是None。
  • refit：在多个score的情况下，模型在进行选择的时候，需要明确的scoring依据。
• n_jobs：与并行运行相关，即可以提高搜索速度，取值为整数，默认为1，大于1的整数表示运行核数（但不能超过运行主机有的核数），取-1代表使用主机所有的核数。默认是None。
• cv：交叉验证的折数。默认是None，即5折。
• return_train_score：应该是控制是否返回得分。默认是False。

使用：

• .fit：进行具体的搜索，且会返回搜索器实例本身信息；
• .best_estimator_：可以查看带有最优超参的搜索器的相关信息；
• .best_score_：可以查看当前最优超参情况下的得分；
• .best_params_：可以输出当前由最优的超参及其取值组成的字典。

# 引入网格搜索，找到最优模型
from sklearn.model_selection import GridSearchCV

SGDReg = SGDRegressor()

params = [
    'loss': ['squared_error'], 'penalty': ['l1', 'l2'], 'max_iter': [1000, 10000, 30000],  # 第一组参数及其可选择的值
    'loss': ['epsilon_insensitive'], 'penalty': ['l1', 'l2'], 'max_iter': [1000, 10000, 30000]  # 第二组参数及其可选择的值
]  # 根据所要搜索的模型，调整需要搜索的参数
scores = ['r2', 'neg_mean_squared_error']
best_SGDReg = GridSearchCV(SGDReg, param_grid=params, n_jobs=-1, scoring=scores, refit='neg_mean_squared_error')

best_SGDReg.fit(train_x, train_y)

4. 完整代码

完整代码如下：

import pandas as pd
from Data_processing_by_Pandas import mango_processing
from Regression_Model_evaluation import regression_evaluation_without_cross
from Regression_Model_evaluation import regression_evaluation_with_cross

# 读取数据
train = pd.read_csv('train.csv', nrows=50000)
print(train.describe())

train_target = train['fare_amount']
train_feature_before = train.drop(['key', 'fare_amount', 'pickup_datetime'], axis=1)

# 进行数据处理
train_feature = mango_processing(train_feature_before)

# 划分训练集与测试集
from sklearn.model_selection import train_test_split
train_x, test_x, train_y, test_y = train_test_split(train_feature, train_target, test_size=0.2, random_state=42)

# 引入网格搜索，找到最优模型
from sklearn.model_selection import GridSearchCV
from sklearn.linear_model import SGDRegressor

SGDReg = SGDRegressor()

params = [
    'loss': ['squared_error'], 'penalty': ['l1', 'l2'], 'max_iter': [1000, 10000, 30000],  # 第一组参数及其可选择的值
    'loss': ['epsilon_insensitive'], 'penalty': ['l1', 'l2'], 'max_iter': [1000, 10000, 30000]  # 第二组参数及其可选择的值
]  # 根据所要搜索的模型，调整需要搜索的参数
scores = ['r2', 'neg_mean_squared_error']
best_SGDReg = GridSearchCV(SGDReg, param_grid=params, n_jobs=-1, scoring=scores, refit='neg_mean_squared_error')

# 进行网格搜索
best_SGDReg.fit(train_x, train_y)

# 得到相关参数：
print(best_SGDReg.best_score_)
print(best_SGDReg.best_params_)

# 模型训练及预测：
# 将最优模型传入fare_SGD
fare_SGD = best_SGDReg.best_estimator_
fare_SGD.fit(train_x, train_y)
# 模型预测
train_result = fare_SGD.predict(train_x)

# 训练集预测结果评价(个人构建的模型，见上)
regression_evaluation_without_cross(train_y, train_result)
# 测试集交叉验证评价（个人构建的模型，见上）
regression_evaluation_with_cross(fare_SGD, train_x, train_y)