机器学习入门 ----线性回归模型及其Python代码解析

Posted 2021-05-09 找不到服务器～～

机器学习入门

----线性回归模型及其Python代码解析

文章目录

• 机器学习入门
• ----线性回归模型及其Python代码解析
• • 一.前言
  • 二.线性回归模型的描述
  • • 1.线性回归模型到底有什么用途呢？（引入概念的废话）
    • 2.线性回归模型的数学解释（不是废话）
    • • 数据集输入
      • 公式化
      • 损失函数
      • 梯度下降法
  • 三.线性回归模型的python简单实现及其解析
  • • • 1.线性回归类的构造函数
      • 2.梯度下降算法函数
      • • 批量梯度下降算法（BGD）函数：
        • 随机梯度下降算法(SGD)函数
        • 辅助函数1：Shuffle_Sequence()
      • 3.迭代训练函数
      • • train_BGD（）函数
        • train_SGD()函数
        • 辅助函数2：Cost()
      • 4.预测与测试函数
      • • predict()函数：
        • test()函数：
      • 5.实际数据操作
  • 四.缺点分析

一.前言

（1） 最近MDG小组在研究机器学习中神经网络的内容，在学习过程中遇到一些必需，也挺有趣的模型，为了能够打好基础，并且仔细思考模型的实现过程，所以写这篇博客来总结一下~
（2） 另外我的第一篇博客（C语言实现排序算法二迟迟未出），因为后面的排序算法写起来可能比较费时间，而且重要性不是很强，因此我有时间一定把二给出了~
（3） 因为在该模型的推导过程中涉及到了一些概率论的知识，我对此无能为力，因此在这一部分会简单略过哟~

二.线性回归模型的描述

1.线性回归模型到底有什么用途呢？（引入概念的废话）

线性回归模型的可用之地可以说是非常的广泛，在金融，传染病分析，数学，经济学等领域都发挥着非常巨大的作用。在我看来线性回归模型其中一个很大的用处便是他的预测功能，只要给他提供大量的训练数据和测试数据，通过大量的迭代训练，最终产生一个较为成熟的模型。此时再给这个模型输入一个数据，这个模型便可以返回一个预测值。那有人就会提出疑问了，那有什么稀奇的，不就是给我返回一个预测值嘛，能有多大用处咧?预测不能说正确率是百分百的，但是它能够让我们的世界被数据武装起来，一切都以科学至上。它能够让我们未雨绸缪，做出更加正确的决策…那这里就不多说，毕竟这不是重点，下面我将开始解释线性回归模型。

2.线性回归模型的数学解释（不是废话）

数据集输入

给定输入数据集D：

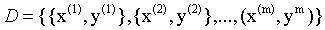
m表示输入数据集大小，x(i)表示一组输入数据：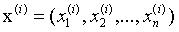
可以这么理解，$x^{(i)}$有n个属性：
比如说：给你一头牛，这头牛就对应$x^{(i)}$，而$x_1^{(i)}$可能对应牛的体重，$x_2^{(i)}$可能对应牛的脂肪率，以此类推，这些因素共同影响牛的价格$y^{(i)}$。
$y^{(i)}$ 为 $x^{(i)}$ 对应的真实结果。

线性回归主要是想找到一个相关属性的线性组合，从而进行预测。

公式化

那接下来要做的工作就是将上述过程公式化：

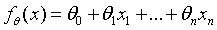
式子中的${\theta }_i$表示线性回归的模型参数，$x_i$表示输入数据，那么$f_{\theta }(x)$就可以表示为θ向量和x向量属性的乘积了，如下：

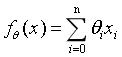
这里的$f_{\theta }(x)$算出来其实就是预测值，我们要做的工作就是尽可能地让这些算出来的预测值逼近一开始输入电脑的数据集。
那么问题来了：如何来衡量这个预测值已经接近真实值（就是一开始输入的数据集中的$y^{(i)}$）了呢？

损失函数

所以这里引入了一个函数$J(\theta )$，名为损失函数，听这名字就很酷炫！！
我们再来看看他长什么样子：

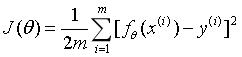
同学不要走啊~，这个公式没那么可怕，这是一个最小二乘法的应用，含义就是让每一个预测值减去每一个真实值然后再平方，然后再除以2*数据及大小。这样得出的结果可以用于描述数据拟合的程度。所以，再次明确我们的目标：找到一个合适的θ向量，让损失函数$J（\theta ）$的值达到最小，因此有了目标就有了问题：如何找到这样的θ向量呢？

梯度下降法

梯度下降算法最普遍的有三种：批量梯度下降算法，随机梯度下降算法，小批量梯度下降算法。我这里只介绍批量梯度下降算法，后续python代码实现的部分将会覆盖这三种算法。这里我找到一篇写的比较详细的博客，所以我就不费神自己写了，我直接照搬了他的图：

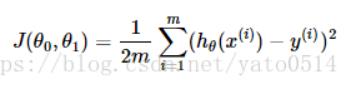
他这个式子中，损失函数的参数有两个θ（${\theta }_0,{\theta }_1$），这不是一个大问题，因为在我前面的叙述中我把θ当成了一个向量，将整个向量作为了参数输入，他这里只是将向量中的每一个元素单独抽出来输入而已~

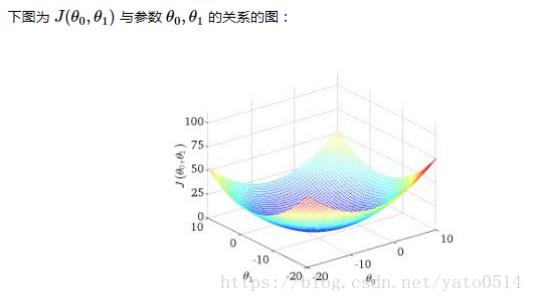
这个图就是损失函数对应的立体图形了，它是一个类似碗（半边屁股）的形状，诶这就好了，因为我们要做的工作不恰恰是找到那个损失函数的最小值嘛！那不就是碗底吗（屁股尖）！！问题来了：怎么得到这个最小值？梯度下降算法的用处就来了，在讲述梯度下降算法在三维空间中的应用之前，我先来讲述一下二维空间的故事。高中老师扔给你一道题，给你一个开口朝上的函数你给我找出它的最小值，怎么找啊，对，求导！导数为0的点不就是最小值点嘛。于是回到了三维空间，你尝试对损失函数求导，咦，怎么有两个参数咧？切，不久求偏导数咯~求导过程如下：

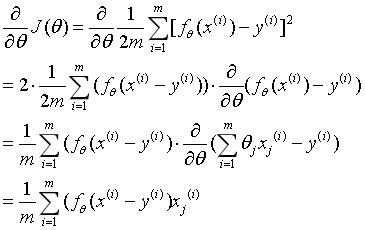
日，为什么我自己写的公式都有水印！

然后你又发现了一个问题：求导求出来不是一个导函数吗，我怎么知道我代入哪一个θ，其实这里初始θ是随机给出的，你要做的工作是反复更新θ的值，让损失函数达到最小，这里给出更新公式：

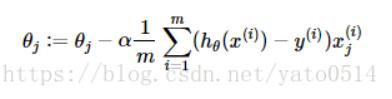
：=表示更新的意思
上面公式的$h_{\theta }(x)$与我写的$f_{\theta }(x)$是一样的
α表示学习率，就是每次更新的步长，由你来设定
两种情况：
（1）θ只有一个：
则偏导数等价于导数（因为只对一个变量求导），我们知道导数可以表示方向，这个更新公式中导数用来指明最低点的方向，而学习率才表示θ更新的速率，因此根据实际情况，我们得到一个损失函数时可以根据这个函数的图像，观察它的陡峭情况，从而确定一个较为合适的学习率。
（2）θ有多个：
那也很简单，只要把公式中作为一个单独的数的θ改变成一个包含多个数的θ向量进行计算即可，这样就可以转变成一个单线程的问题。

关于这个梯度下降算法的详细解释有几篇写得很好的博客，这里推荐一下：
机器学习入门——梯度下降算法详解

批量梯度下降法（BGD）、随机梯度下降法（SGD）和小批量梯度下降法（MBGD）
好了，关于线性回归的比较基础的数学问题就叙述到这，现在开始进行线性回归模型python代码实现的解析。

三.线性回归模型的python简单实现及其解析

Python中实现一个模型的方法通常是建立一个专门的类，在类当中添加不同的方法，那么这里首先就建立一个线性回归的类：
本代码中需要导入numpy库

1.线性回归类的构造函数

功能：完成训练数据集，训练结果集和线性回归的模型参数初始化

import numpy as np

class LinearRegression(object):
    def __init__(self,input_data,realresult,theta=None):
        """
        :param input_data: 训练数据集（二维列表）
        :param realresult: 训练结果集
        :param theta: 线性回归的模型参数，就是数据集在线性方程中的系数向量
        """
        #获得数据集的形状
        row,col=np.shape(input_data)    #row代表数据x的个数，col代表一个x中属性的个数
        #构造输入数据数组
        self.InputData = [0]*row        #开辟一个数据列表，元素个数为数据点的个数,否则后面不能够使用InputData[index]=Data的语法
        #给每组输入数据增添常数项1
        for(index,data) in enumerate(input_data):   #data代表了一个数据点的x数据
        	#首先定义Data第一个元素为1.0，这样可以保证θ元素数量和Data元素数量相同，这个1.0对应与偏置量相乘
            Data=[1.0]
            Data.extend(list(data))
            self.InputData[index]=Data
        self.InputData = np.array(self.InputData)   #将InputData从二维列表转换成数组类型
        #构造输入数据对应的结果
        self.Result=realresult
        self.Result = np.array(self.Result)
        #参数theta不为None时，利用theta构造模型参数
        if theta is not None:
            self.Theta = theta
        else:
            #随机生成服从标准正态分布的参数
            self.Theta=np.random.normal(size=(col+1,1))

解析：
虽然我已经在代码块中进行了必要的注释，但这里我还是做一下简单的解释：

1.1：
首先需要关注__init__方法的输入参数，

• input_data:输入数据集，也就是x，其中这个数据集是一个二维列表，因为前面已经解释过，一个数据集包含了多个x，而每一个x又包含了多个属性。因此列表的第一维表示不同的x，第二维则表示x包含的不同属性，例：
  $[[x_1^{(1)},x_2^{(1)},x_3^{(1)}],[x_1^{(2)},x_2^{(2)},x_3^{(2)}],[x_1^{(3)},x_2^{(3)},x_3^{(3)}]]$
• realresult:输入真实结果集，也就是每一个x真实对应的y
• theta:线性回归参数，就是前面提到的θ向量，对于只有一个变量时，θ是一个数，数据类型也是一维列表。

1.2构造函数中新建立的变量：

• row,col:描述输入的数据集形状，row表示x属性的个数,col表示x的个数
• self.InputData:将输入的数据x转换为数组形式，方便后续进行向量运算，这里要强调一下,InputData的形式如下：
  [[1.0,x1],[1.0,x2],[1.0,x3]…]
• self.Result:用于存储输入的真实结果
• self.Theta:传入用户输入的θ，若用户没有输入，则按照随机标准正态分布来定义初始模型参数。

1.3用户未输入θ时，运用normal()函数生成随机标准正态分布的θ
normal函数的参数：

• loc(float):正态分布的均值
• scale(float):正态分布的标准差
• size(int或整数元组)

到此处，线性回归模型的构造函数就完成了，接下来需要编写梯度下降算法的实现函数，以达到更新θ向量，从而使损失函数最小的目的。

2.梯度下降算法函数

梯度下降算法分为三种，分别是：批量梯度下降算法(BGD)，随机梯度下降算法(SGD)，小批量梯度下降算法(MBGD)。这里将对前两种算法进行python代码实现，毕竟篇幅有限，第三种大家可以自己了解~

批量梯度下降算法（BGD）函数：

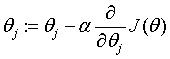
批量梯度下降算法中的偏导数采用了平均梯度增量，这样就需要遍历输入数据，并计算出平均值，然后再开始更新θ的过程。

 def BGD(self,alpha):
        """
        BGD批量梯度下降算法进行一次迭代调整线性回归模型参数的函数
        :param alpha:学习率
        :return:
        """
        #定义梯度增量数组
        gradient_increasment=[]
        #对输入的训练数据及其真实结果进行依次遍历
        for(input_data,real_result) in zip(self.InputData,self.Result):
            #计算每组input_data的梯度增量，并放入梯度增量数组
            g = (real_result-input_data.dot(self.Theta))*input_data  #self.Theta是一个系数向量，dot()进行点积运算
            gradient_increasment.append(g)
        #按列计算属性的平均梯度增量
        avg_g = np.average(gradient_increasment,0)
        #改变平均梯度增量数组的形状
        avg_g=avg_g.reshape((len(avg_g),1))	#转置向量，因为Theta是一个列向量
        #更新模型参数self.Theta，套用公式
        self.Theta = self.Theta+alpha*avg_g

BGD.1：传入参数
alpha:这就是前面提到的学习率

BGD.2：函数中变量和计算过程解释

• gradient_increasment:梯度增量数组
• g:

遍历构造函数中整理好的InputData和Result，遍历结果分别存入input_data和real_result中
dot()进行点积运算，因为input_data是一个np.array类型，所以可以直接进行向量数乘运算，与列表有区别

a = np.array([1,2,3]) #数组类型
b = [1,2,3]	#列表类型
print(2*a)	#[2,4,6]
]
print(2*b)	#[1,2,3,1,2,3]

g计算的含义：
我猜你又忘了梯度增量怎么计算了，回顾一下这个图：

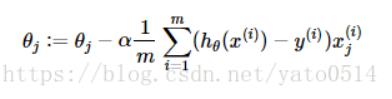
g计算的是每一个数据x的梯度增量，遍历所有的x，计算出所有的g，把这些g放进梯度增量数组gradient_increasment中，然后再进行average()运算，算出平均梯度增量，代入公式即可。

随机梯度下降算法(SGD)函数

相比于批量梯度下降算法，随机梯度下降算法的收敛速度更快，属于贪心算法，最终求得的是次优解，而不是全局最优解。所以随机梯度下降算法理论上得到的解是再全局最优解的附近区域内振荡。

    def SGD(self,alpha):
        """
        随机梯度下降算法函数
        :param alpha: 学习率
        :return:
        """
        #首先将数据集打乱，减少数据集顺序对参数调优的影响
        shuffle_sequence = self.Shuffle_Sequence()
        self.InputData = self.InputData[shuffle_sequence]   #通过将产生的随机自然序列元素作为索引来随机获得数据
        self.Result = self.Result[shuffle_sequence]
        #对数据集进行遍历，利用每组训练数据对参数进行调整
        for(input_data,real_result) in zip(self.InputData,self.Result):
            #计算每组input_data的梯度增量
            g = (real_result-input_data.dot(self.Theta))*input_data
            #调整每组input_data的梯度增量的形状
            g= g.reshape(len(g),1)
            #更新线性回归的模型参数
            self.Theta = self.Theta + alpha * g

SGD函数的实现思路与BGD函数的实现思路大同小异，只是在更新公式的层面上，梯度增量的计算方法有差别。
要实现SGD，首先需要构造一个辅助函数Shuffle_Sequence()，它的作用是生成与训练数据集大小相同的随即自然数序列。这样我们就可以打乱训练集和他的结果集，从而消除训练集顺序对SGD算法优化参数的影响。

辅助函数1：Shuffle_Sequence()

该辅助函数用于随机打乱原数据集

    def Shuffle_Sequence(self):
        """
        运行SGD算法和MBGD算法之前，随机打乱原始数据集的函数
        :return:已经打乱的自然数序列
        """
        #首先获得数据集的规模，然后按照规模生成自然数序列
        length = len(self.InputData)    #length表示InputData数据x的个数
        random_sequence = list(range(length))   #生成自然数序列0~length-1
        #利用numpy的随机打乱函数打乱训练数据下标
        random_sequence = np.random.permutation(random_sequence)
        print(random_sequence)
        return random_sequence	#返回了一个自然数集，我们可以把它看成一个标签集，random_sequence是np.array类型

注释已经写的比较清楚，这里不多作介绍。
现在来介绍如何实现数据的打乱过程：
因为我们已经通过辅助函数Shuffle_Sequence()生成了一个乱序的自然数集（大小和数据集大小按相同），并且他是一个np.array类型，因此直接放进self.InputData的索引中，便可以直接打乱顺序。

可以观察到在SGD函数中，更新过程写在了for循环内部，这样写的意思是每次只对当前遍历到的数据计算梯度增量。

以上便是随机梯度下降算法相较于批量梯度下降算法多写的一步，随机打乱训练数据。下面更新θ的过程是一样的，另外在SGD中不需要计算梯度增量的平均值。

好了，到目前为止，我们已经完成了训练数据初始化，模型参数初始化，构造梯度下降算法函数的工作，接下来要做的工作就是迭代训练数据。

3.迭代训练函数

定义了梯度下降算法函数后再定义迭代训练函数就容易多了，只用定义train_BGD(),train_SGD()函数即可。

train_BGD（）函数

    def train_BGD(self,iter,alpha):
        """
        :param self:
        :param iter:迭代次数
        :param alpha:学习率
        :return:返回了一个包含每次更新后损失函数的值的np.array类型数据
        """
        Cost=[]
        #开始迭代训练
        for i in range(iter):
            #利用学习率alpha，结合BGD算法对模型进行训练
            self.BGD(alpha)
            #记录每次迭代的平均训练损失
            Cost.append(self.Cost())
        Cost = np机器学习入门复习1机器学习导论

 机器学习入门
 机器学习入门
 机器学习入门
 机器学习快速入门简单自学机器学习理论
 机器学习入门 机器学习简介 | 附加小练习