多目标优化问题和遗传算法学习

Posted 2022-02-23 软件工程小施同学

名词：

Nondominated sorting 非支配排序
Nonelitism approach 非精英机制方法
selection operator 选择算子
multicriterion decision-making methods 多重判据决策方法

基本概念：

（1） 多目标优化问题的数学描述

（2）pareto（帕累托）最优解的相关概念

1）Paerot支配关系：

2）Pareto最优解定义：

多目标优化问题与单目标优化问题有很大差异。

当只有一个目标函数时,人们寻找最好的解,这个解优于其他所有解,通常是全局最大或最小,即全局最优解。

而当存在多个目标时,由于目标之间存在冲突无法比较,所以很难找到一个解使得所有的目标函数同时最优,也就是说,一个解可能对于某个目标函数是最好的,但对于其他的目标函数却不是最好的,甚至是最差的。

因此,对于多目标优化问题,通常存在一个解集,这些解之间就全体目标函数而言是无法比较优劣的,其特点是:无法在改进任何目标函数的同时不削弱至少一个其他目标函数。这种解称作非支配解(nondominated soluitons)或Pareto最优解(Pareto optimal Soluitons),定义如下：

NSGAII算法：

（1）NSGAII算法的基本流程

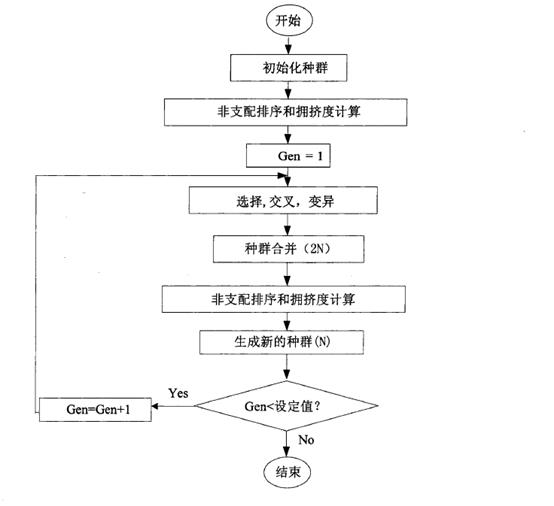
首先,随机产生规模为N的初始种群,非支配排序后通过遗传算法的选择、交叉、变异三个基本操作得到第一代子代种群;

其次,从第二代开始,将父代种群与子代种群合并,进行快速非支配排序,同时对每个非支配层中的个体进行拥挤度计算,根据非支配关系以及个体的拥挤度选取合适的个体组成新的父代种群;

最后,通过遗传算法的基本操作产生新的子代种群:依此类推,直到满足程序结束的条件。相应的程序流程图如下图所示：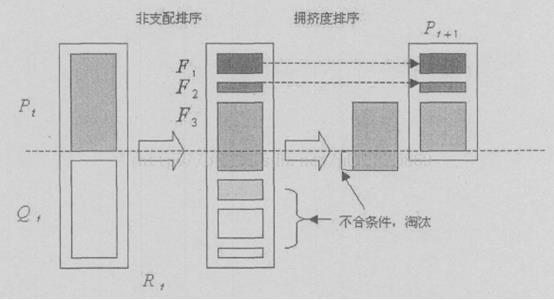

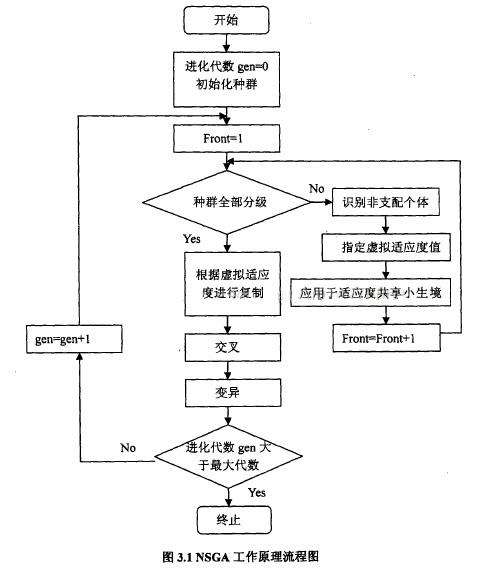
（2）三个关键步骤：

算法思想：

A. 快速非支配排序方法

O(MN3)方法：确定非支配前沿面，每一个解与其他解比较判断是否支配，故每个解的时间复杂度是O（MN），要找到第一前沿面需要判断每个解，故时间复杂度是O（MN2），要找到所有的前沿面最坏的时间复杂度是O（MN3）。
本文提出的O（MN2）方法：

step1. 确定两个实体：np表示被多少解支配，是一个数目，Sp表示该解所支配的解的集合，如下图所示，D点被A和C点支配，所以D点的np为2，A点支配D和E，所以A点的Sp=D，E。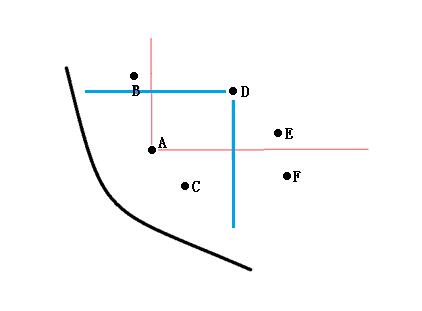

step2. 初始化，两个实体初始化都为0，通过两层循环来获得上述两个实体的值，该步时间复杂度是O（MN2）。
step3 对第一非支配面，即np为0 的解，访问其集合Sp中的每个解然后把其np-1。重复该步，即可得到所有的非支配面。由于每个解最多由N-1个支配，所以每个解被访问的次数最多为N-1次。所以该步时间复杂度为O（N2）。
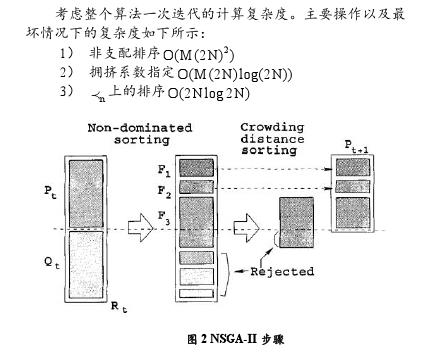
综上所述，NSGA-II提出的计算非支配排序的时间复杂度为O（MN2）。

B. 保留多样性

NSGA-II提出了拥挤比较方法替换了共享函数法。

1）密度估计：根据每一目标函数计算该点两侧的两个点的平均距离，该值作为以最近邻居作为顶点的长方体周长的估计（作为拥挤系数）。如下图，第i个解的拥挤系数为他周围长方体的长度（虚线表示）。计算拥挤系数需要对每一目标函数进行排序。

2）拥挤算子比较：

这里对拥挤系数的算法展示一下：
其中 I[i].m 代表集合I中第i个个体第m个目标函数值。I[i]越大代表该点的密度小，越容易被选中。

C. 主程序

先按照非支配面进行排序，然后对每个支配面里的拥挤算子进行排序，找出前N个点，主要思想如上述B里的第二点。

仿真：

（1）测试函数

1）ZDT问题

2）DTLZ问题

（2）评估指标

所有目标函数都是求最小化（convex 凸的，nonconvex 非凸的）
1）评估解收敛性，用deb提出的Convergence Metric（收敛性指标）

2）评估解分布的均匀性，用Schott提出的Spacing Metric（间距指标）

3）SBX: 模拟二进制交叉（SBX,simulated binary crossover），遗传算法采用浮点数编码的时候可以使用。

4）多项式变异:

（3）仿真流程：

仿真代码已上传至：NSGA-II.zip-算法与数据结构文档类资源-CSDN下载
MATLAB代码，可以完美运行无错误，需要的朋友可以下载，已附上文章可供参考学习。

参考文献

[1] K. Deb, A. Pratap, S. Agarwal and T. Meyarivan, “A fast and elitist multiobjective genetic algorithm: NSGA-II,” in IEEE Transactions on Evolutionary Computation, vol. 6, no. 2, pp. 182-197, April 2002, doi: 10.1109/4235.996017.
[2]公茂果,焦李成,杨咚咚,等.进化多目标优化算法研究[J].软件学报,2009(2):271-289.