遗传算法(geatpy)
Posted hellobigorange
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了遗传算法(geatpy)相关的知识,希望对你有一定的参考价值。
文章目录
参考博客:https://blog.csdn.net/weixin_37790882/article/details/84034956
遗传算法
被用来进行目标优化的,即选择什么样的个体时,可以使目标值最高,优胜劣汰
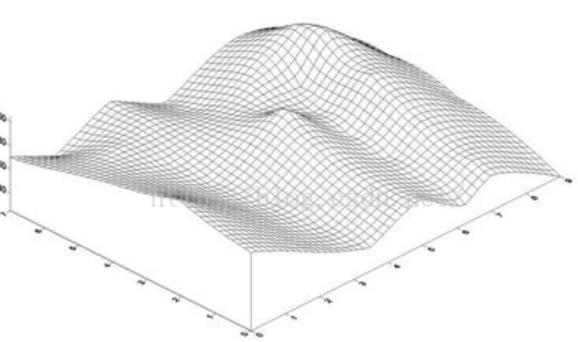
遗传算法中每一条染色体,对应着遗传算法的一个解决方案,一般我们用适应性函数(fitness function)来衡量这个解决方案的优劣。所以从一个基因组到其解的适应度形成一个映射。可以把遗传算法的过程看作是一个在多元函数里面求最优解的过程。 可以这样想象,这个多维曲面里面有数不清的“山峰”,而这些山峰所对应的就是局部最优解。而其中也会有一个“山峰”的海拔最高的,那么这个就是全局最优解。而遗传算法的任务就是尽量爬到最高峰,而不是陷落在一些小山峰。(另外,值得注意的是遗传算法不一定要找“最高的山峰”,如果问题的适应度评价越小越好的话,那么全局最优解就是函数的最小值,对应的,遗传算法所要找的就是“最深的谷底”
计算 x + 16 ∗ s i n ( 5 ∗ x ) + 10 ∗ c o s ( 4 ∗ x ) x + 16 * sin(5 * x) + 10 * cos(4 * x) x+16∗sin(5∗x)+10∗cos(4∗x)的最大值,x在区间(5,20)内,
# -*- coding: utf-8 -*-
import numpy as np
import matplotlib.pyplot as plt
# 适应度函数,目标函数,求取最大值
def fitness(x):
return x + 16 * np.sin(5 * x) + 10 * np.cos(4 * x)
# 个体类
class indivdual:
def __init__(self):
self.x = 0 # 染色体编码
self.fitness = 0 # 个体适应度值
def __eq__(self, other):
self.x = other.x
self.fitness = other.fitness
# 初始化种群
# pop为种群适应度存储数组,N为个体数
def initPopulation(pop, N):
for i in range(N):
ind = indivdual() # 个体初始化
ind.x = np.random.uniform(-10, 10) # 个体编码。-10,10的正态分布,可以自己设定限定边界
ind.fitness = fitness(ind.x) # 计算个体适应度函数值
pop.append(ind) # 将个体适应度函数值添加进种群适应度数组pop
# 选择过程
def selection(N):
# 种群中随机选择2个个体进行变异(这里没有用轮盘赌,直接用的随机选择)
return np.random.choice(N, 2)
# 交叉/重组过程
def crossover(parent1, parent2):
'''
这里选用了线性交叉重组VarChild[i] = VarParent1[i] ·α + VarParent2[i] ·(1−α),i ∈ [1,2,...,N]
:param parent1: 父辈1
:param parent2: 父辈2
:return: 经过交叉后的子辈1,子辈2
'''
child1, child2 = indivdual(), indivdual() # 父亲,母亲初始化
child1.x = 0.9 * parent1.x + 0.1 * parent2.x # 交叉0.9,0.1,可以设置其他系数
child2.x = 0.1 * parent1.x + 0.9 * parent2.x
child1.fitness = fitness(child1.x) # 子1适应度函数值
child2.fitness = fitness(child2.x) # 子2适应度函数值
return child1, child2
# 变异过程
def mutation(pop):
'''
:param pop: 种群列表
:return: 从种群中挑选一个个体进行变异
'''
# 种群中随机选择一个进行变异
ind = np.random.choice(pop)
# 用随机赋值的方式进行变异
ind.x = np.random.uniform(5, 20) # 均匀分布
ind.fitness = fitness(ind.x)
# 最终执行
def implement():
# 种群中个体数量
N = 40
# 种群
POP = []
# 迭代次数
iter_N = 400
# 初始化种群
initPopulation(POP, N)
# 进化过程
for it in range(iter_N): # 遍历每一代
a, b = selection(N) # 随机选择两个个体作为父辈
if np.random.random() < 0.65: # 以0.65的概率进行交叉结合
child1, child2 = crossover(POP[a], POP[b])
new = sorted([POP[a], POP[b], child1, child2], key=lambda ind: ind.fitness,
reverse=True) # 依据函数值,将父母亲和子代进行比较,保留最好的两个(值最大的)
POP[a], POP[b] = new[0], new[1] # 种群总数量不变,优胜劣汰
if np.random.random() < 0.1: # 以0.1的概率进行变异
mutation(POP)
return POP
if __name__ == '__main__':
pop = implement()
# 绘图代码
def func(x):
return x + 16 * np.sin(5 * x) + 10 * np.cos(4 * x)
x = np.linspace(5, 20, 100000)
y = func(x)
scatter_x = np.array([ind.x for ind in pop])
scatter_y = np.array([ind.fitness for ind in pop])
best = sorted(pop, key=lambda pop: pop.fitness, reverse=True)[0] # 最佳点
print('best_x', best.x)
print('best_y', best.fitness)
plt.plot(x, y)
# plt.scatter(scatter_x, scatter_y, c='r')
plt.scatter(best.x, best.fitness, c='g', label='best point')
plt.legend()
plt.show()
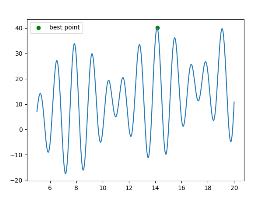
best_x 14.155236796527797
best_y 40.06386706919228
geatpy实现遗传算法
geatpy的官方文档:http://geatpy.com/index.php/details/
geatpy官网:http://www.geatpy.com
文章参考:https://blog.csdn.net/weixin_37790882/article/details/84034956
准备工作:安装geatpy包
pip install geatpy
一、基础术语
1、个体
- 个体染色体:决策变量编码后得到的行向量,如二级制编码(决策变量)x1=010,x2=001,个体[x1,x2]
- 个体表现型:对个体染色体进行解码,如上述解码x1=2,x2=1; “1 2”,它就是个体的表现型
- 染色体区域描述器
注:可以进行实际值编码,此时个体染色体等同个体表现型。
2、种群
-
种群染色体矩阵:矩阵每一行代表一个个体
-
种群表现型矩阵:对种群染色体矩阵解码
-
种群个体违反约束矩阵(CV):它每一行对应一个个体,每一列对应一种约束条件(可以是等式约束或不等式约束)。CV矩阵中元素小于或等于0表示对应个体满足对应的约束条件,大于0则表示不满足,且越大表示违反约束条件的程度越高。比如有两个约束条件:
x 1 + 2 x 3 < = 2 x_1+2x_3<=2 x1+2x3<=2
x 1 + x 2 + x 3 = 1 x_1+x_2+x_3=1 x1+x2+x3=1
-
如何计算CV矩阵?可以创建两个列向量CV1和CV2,然后把它们左右拼合而成一个CV矩阵。
import numpy as np
"""phen为种群表现性矩阵,由4个个体组成"""
phen = np.array([[1, 0, 0], [1.1, 1, 2], [2, -3.1, 2.1], [1, -1, 0]])
"""x1,x2,x3为决策变量"""
x1 = phen[:, 0]
x2 = phen[:, 1]
x3 = phen[:, 2]
"""计算CV矩阵"""
cv1 = x1 + 2*x2 - 2 # 不等式约束
cv2 = np.abs(x1 + x2 + x3 - 1) # 等式约束,加绝对值,就可以保证CV矩阵的值只有等于0满足约束
CV = np.vstack((cv1,cv2)).T # 上下合并两个行向量,并转置
print("种群约束矩阵:\\n",CV)
种群约束矩阵:
[[-1. 0. ]
[ 1.1 3.1]
[-6.2 0. ]
[-3. 1. ]]
由此可见,第一个个体满足两个约束条件;第二个个体违反了2个约束条件;第三和第四个个体满足第一个约束条件但违反了第二个约束条件。
下面学一下:geatpy包创建真实值染色体矩阵
import numpy as np
from geatpy import crtpc
# help(crtpc) # 查看帮助
Nind = 7 # 定义种群规模(个体数目)
Encoding = 'RI' # 表示采用“实整数编码”,即变量可以是连续的也可以是离散的
# 创建“区域描述器”,表明有4个决策变量,范围分别是[-3.1, 4.2], [-2, 2],[0, 1],[3, 3],
# FieldDR第三行[0,0,1,1]表示前两个决策变量是连续型的,后两个变量是离散型的
FieldDR=np.array([[-3.1, -2, 0, 3],
[ 4.2, 2, 1, 5],
[ 0, 0, 1, 1]])
# 调用crtri函数创建实数值种群
Chrom=crtpc(Encoding, Nind, FieldDR)
print("实值染色体矩阵:\\n",Chrom)
实值染色体矩阵:
[[-3.05633545 0.20690918 -0. 5. ]
[ 1.90761108 -0.27868652 1. 5. ]
[ 3.21710205 0.72753906 -0. 3. ]
[-2.36126709 1.80065918 1. 5. ]
[ 0.56381226 -0.3190918 0. 5. ]
[ 2.30549316 -0.3861084 0. 5. ]
[ 1.51663513 -1.08215332 -0. 3. ]]
这里要插入讲一下**“区域描述器”(见上述代码中的FieldDR),它是用于描述种群染色体所表示的决策变量的一些信息,如变量范围、连续/离散性。另外还有一种区域描述器(FIeldD),用于描述二进制/格雷码的种群染色体。FieldDR和FieldD两个合称“Field”,又可以认为它们是“译码矩阵”**。FieldDR具有以下的数据结构:

代码1中的FieldDR矩阵的第三行即为这里的varTypes。它如果为0,表示对应的决策变量是连续型的变量;为1表示对应的是离散型变量。
***下面学习一下构建一个二进制种群染色体矩阵:***

- lens: 每个决策变量编码后在染色体中所占的长度。
- lb: 指明每个变量使用的下界。
- ub: 指明每个变量使用的上界。
- codes: (0:binary | 1:gray) 指明子串是怎么编码的,0为标准二进制编码,1为格雷编码。
- scales: (0: rithmetic | 1:logarithmic) 指明每个子串是否使用对数或算术刻度,1为使用对数刻度,0为使用算术刻度。
- lbin: (0:excluded | 1:included)。
- ubin: (0:excluded | 1:included)。
- varTypes: (0:continued | 1:discrete)。
- lbin和ubin指明范围中是否包含每个边界。lbin=0或ubin=0,表示范围中不包含相应边界;lbin=1或ubin=1,表示范围中包含相应边界。
注意:对于二进制编码,二进制种群的染色体具体代表决策变量的什么含义是不由染色体本身决定的,而是由解码方式决定的。因此在创建二进制种群染色体之初就要设定好译码矩阵(又称“区域描述器”)。
import numpy as np
from geatpy import crtpc
# help(crtpc) # 查看帮助
# 定义种群规模(个体数目)
Nind = 4
Encoding = 'BG' # 表示采用“二进制/格雷”编码
# 创建“译码矩阵”
FieldD_2 = np.array([[3, 2,3], # 各决策变量编码后所占二进制位数,3个决策变量,长度3,2,3
[0, 0,0], # 各决策变量的范围下界
[7, 3,7], # 各决策变量的范围上界
[0, 0,0], # 各决策变量采用什么编码方式(0为二进制编码,1为格雷编码)
[0, 0,0], # 各决策变量是否采用对数刻度(0为采用算术刻度)
[1, 1,1], # 各决策变量的范围是否包含下界(对bs2int实际无效,详见help(bs2int))
[1, 1,1], # 各决策变量的范围是否包含上界(对bs2int实际无效)
[0, 0,0]])# 表示两个决策变量都是连续型变量(0为连续1为离散)
# 调用crtpc函数来根据编码方式和译码矩阵来创建种群染色体矩阵
Chrom_2=crtpc(Encoding, Nind, FieldD_2)
print("二进制染色体矩阵:\\n", Chrom_2)
二进制染色体矩阵:
[[0 0 0 1 0 0 0 0]
[0 1 0 0 1 1 1 1]
[0 0 1 0 0 0 1 0]
[1 1 0 1 1 0 1 0]]
3、编码和解码
对于二进制编码染色体矩阵需要解码,实值染色体矩阵未编码,因此不需要解码。
对上述的二进制种群染色体矩阵Chrom_2和FieldD译码矩阵进行译码可得:
from geatpy import bs2ri
# help(bs2ri)
Phen = bs2ri(Chrom_2, FieldD_2)
print('表现型矩阵 = \\n', Phen)
表现型矩阵 =
[[0. 2. 0.]
[2. 1. 7.]
[1. 0. 2.]
[6. 3. 2.]]
4、目标函数值
种群的目标函数值存在一个矩阵里面(一般命名为ObjV),它每一行对应一个个体的目标函数值。对于单目标而言,这个目标函数值矩阵只有1列,而对于多目标而言,就有多列了,比如下面就是一个含两个目标的种群目标函数值矩阵:
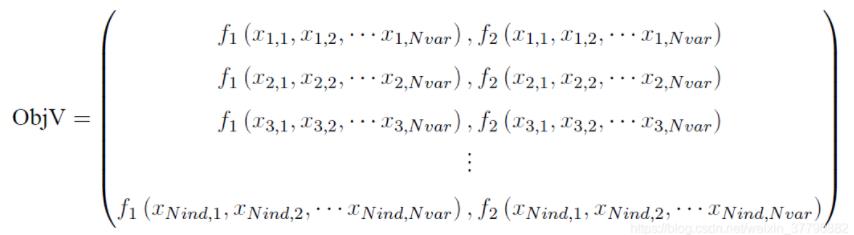
(这里Nind表示种群的规模,即种群含多少个个体;Nvar表示决策变量的个数)
def get_aim(phen):
x1=phen[:,[0]] # 所有的个体决策变量x1
x2=phen[:,[1]] # 所有的个体决策变量x2
x3=phen[:,[2]] # 所有的个体决策变量x3
f=x1+x2+x3 # 目标函数值f
cv= np.abs(x1+x2+x3-2) # 种群个体约束条件矩阵
return f,cv
f,cv = get_aim(Phen)
print("目标函数值f:\\n",f,"\\n个体约束条件矩阵cv:\\n",cv)
目标函数值f:
[[ 2.]
[10.]
[ 3.]
[11.]]
个体约束条件矩阵cv:
[[0.]
[8.]
[1.]
[9.]]
由上述可以看出,个体1的目标值为2,满足cv约束条件
5、适应度值
适应度值通俗来说就是对种群个体的”生存能力的评价“。对于简单的单目标优化,我们可以简单地把目标函数值直接当作是适应度值(注意:当用geatpy遗传和进化算法工具箱时,则需要对目标函数值加个负号才能简单地把它当作适应度值,因为geatpy遵循的是”目标函数值越小,适应度值越大“的约定。)
对于多目标优化,则需要根据“非支配排序”或是其他方法来确定种群个体的适应度值
种群适应度:(FitnV):它是一个列向量,每一行代表一个个体的适应度值:

Nind表示种群含多少个个体
from geatpy import ranking
# help(ranking)
f= np.array([[8.],[70.],[10.],[8.]])
cv =np.array([[0.],[0.],[0.1],[1.]])
FitnV = ranking(f, cv)
print('种群适应度矩阵 = \\n', FitnV)
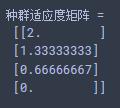
由上述结果可知,在个体cv都满足约束(值<=0)的情况下,目标函数值越大,适应度越低,上述适应度为1>2>3>4。
二、遗传算法基本算子
1、选择
在进化算法中存在两个阶段的选择。第一次是参与进化操作的个体的选择。这个阶段的选择可以是基于个体适应度的、也可以是完全随机地选择交配个体。一旦个体被选中,那么它们就会参与交叉、变异等进化操作。未被选中的个体不会参与到进化操作中。
第二次是常被称为“重插入”或“环境选择”的选择,它是指在个体经过交叉、变异等进化操作所形成的子代(或称“育种个体”)后用某种方法来保留到下一代从而形成新一代种群的过程。这个选择过程对应的是生物学中的” 自然选择”。它可以是显性地根据适应度(再次注意:适应度并不等价于目标函数值)来进行选择的,也可以是隐性地根据适应度(即不刻意去计算个体适应度)来选择。例如在多目标优化的NSGA-II 算法中,父代与子代合并后,处于帕累托分层中第一层级的个体以及处于临界层中的
且拥挤距离最大的若干个个体被保留到下一代。这个过程就没有显性地去计算每个个体的适应度。
经典的选择算子有:“轮盘赌选择”、“随机抽样选择”、“锦标赛选择”、“本地选择”、“截断选择”、“一对一生存者竞争选择”等等

"""举例:锦标赛选择"""
import numpy as np
from geatpy import selecting
# help(selecting)
Chrom=np.array([[1,11,21],
[2,12,22],
[3,13,23],
[4,14,24],
[5,15,25],
[6,16,26],
[7,17,27],
[8,18,28]])
FitnV = np.array([[1.2],[0.8],[2.1], [3.2],[0.6],[2.2],[1.7],[0.2]])
SelCh = Chrom[selecting('tour', FitnV, 6), :] 以上是关于遗传算法(geatpy)的主要内容,如果未能解决你的问题,请参考以下文章