遗传算法存在问题?

Posted 2023-05-08

在遗传算法的路径规划中，初始种群是随机产生的。为了避免陷入局部极值点，种群数量必须达到一定的规模。然而，种群数量大会导致搜索空间大、删除冗余个体的能力差等问题，会严重影响路径规划的速度。 参考技术A ? 在遗传算法的路径规划中，初始种群是随机产生的。为了避免陷入局部极值点，种群数量必须达到一定的规模。然而，种群数量大会导致搜索空间大、删除冗余个体的能力差等问题，会严重影响路径规划的速度。 参考技术B 我对你 比我任何一任都要爱得多你就像这个世界上还存在另外一个我如果说没有你 我估计还在借酒消愁在高楼和大厦的孤城间独自漂流除了不放你走 对你没任何要求在一切能想到的地点和你不断交流该怎么形容你在我心中的地俗渡盐拭窍诰口逃

模糊时间的柔性车间调度问题-Python实现遗传算法求解

目录

1 问题描述

1.1 模糊加工时间的运算

 2 编码解码

 3 算例

4 算法

4.1 文献【2】中算例验证

4 部分代码展示

完整代码：https://github.com/Aihong-Sun/FJSP_FP_GA

---

1 问题描述

        模糊性和灵活性的概念普遍存在于实际制造系统中，因为机器通常具有多种功能，并且无法提前不精确地知道处理时间。因此，研究具有模糊处理时间的柔性调度问题对于实际应用非常重要。        

        FJSPF（the FJSP with Fuzzy Processing time）可以表述如下：有n 个工件要在 m 台机器上加工。每个工件有ni个工序，每个工件必须按确定的路径完成所有工序，每道工序有1台及以上加工工序，工序的加工时间为模糊时间。

1.1 模糊加工时间的运算

        当工序加工时间为模糊时间时，要想能很好的排产出来，比如在甘特图上排产，需要一些模糊数运算操作。这些运算包括加法运算、两个模糊数的最大运算和模糊数的排序方法。加法运算用于计算运算的模糊完成时间。最大操作用于定义操作。另一种方法是比较最大模糊完成时间。

 对于两个三角模糊数（Triangle fuzzy numbers），和,

(1)加法操作：

(2)取大操作：为了衡量三角模糊书的大小关系,, Sakawa等[1]提出判定方法,此后又有许多学者 重新进行了定义. 本文采用Lei[2] 提出的判别规则, 令

 有: 

        1）若F(X)>F(Y),则X>Y.

        2)   若F(X)=F(Y),则比较,若,则X>Y

        3)   若F(X)=F(Y),且,则比较区间大小，如果,则X>Y

 2 编码解码

参考文献[3]

算例如下：

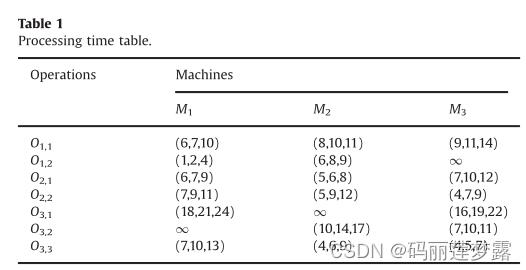
 编码：编码采用OSMS编码，不太知道的可以看我之前写的关于柔性作业车间调度的文章

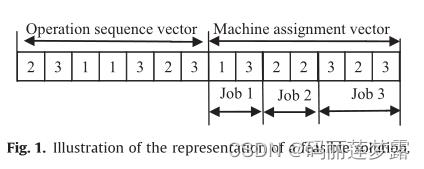
解码：

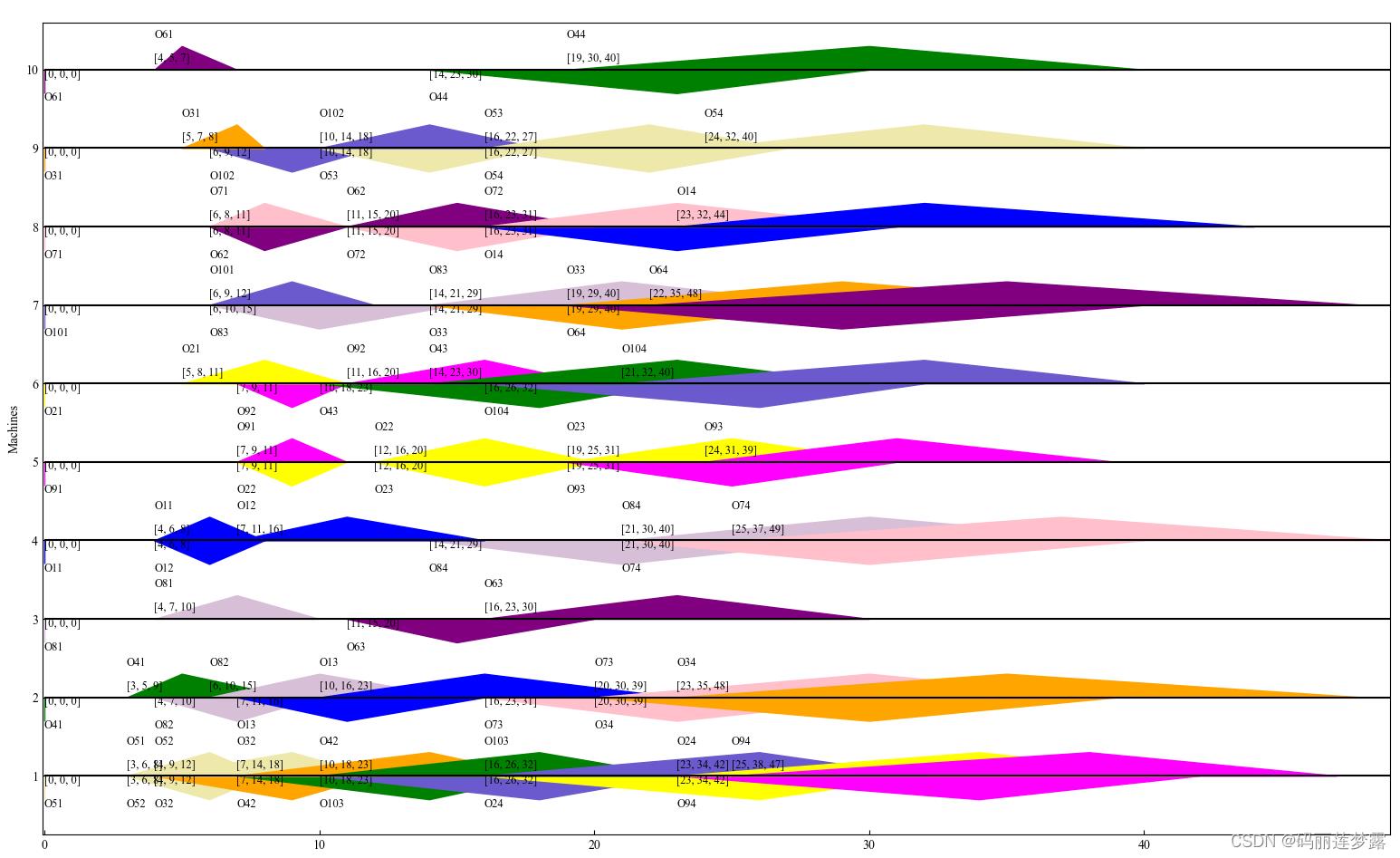
解码前，首先对三角模糊Gantt图进行说明，我们都知道，Gantt图是对各工序在每个机器上加工的开始结束时间进行可视化表述，同理三角模糊Gantt图也是如此，同一横线上的表示一个机器上的工序，横线下方为工序的模糊开始时间，横线上方为工序的模糊结束时间。

普通解码：从左到右读取OS、MS编码，不考虑插入，直接解码

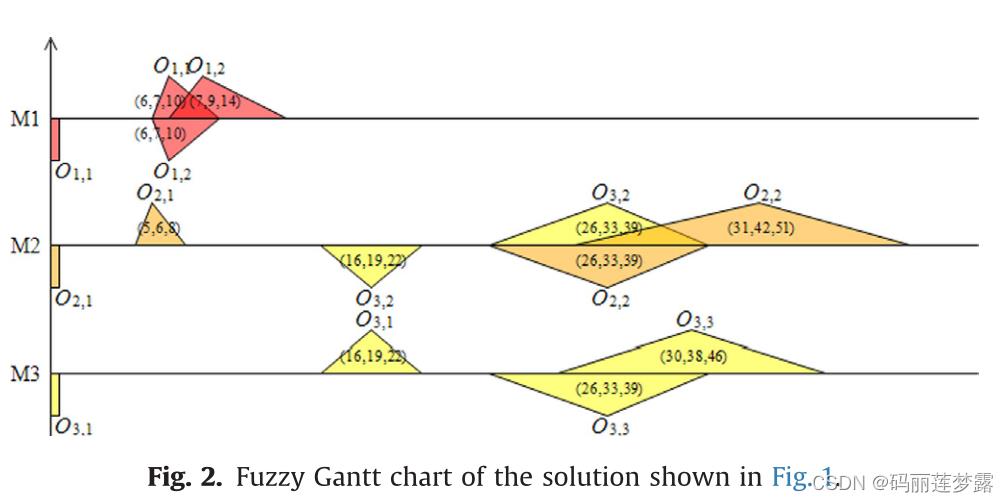
 贪婪解码：考虑工序前插（这跟普通FJSP问题差不多，唯一的区别在于，这里的工序时间是模糊时间）

上诉普通解码的考虑前插后变为：

适应度值为模糊完工时间的三角模糊数：

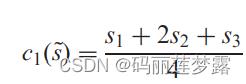
 3 算例

上面给出的文献【2】中提供了4个算例。（单目标），我也对算例进行了整理，需要的可前往此处获取：Aihong-Sun/Fuzzy_time_FJSP_Instance: Instance from <A genetic algorithm for flexible job shop scheduling with fuzzy processing time> (github.com)文献[3]中提供了以完工时间、加工成本、设备负载平衡和加工能耗为目标的多目标算例:

Fuzzy_time_FJSP_Instance/base_instance.py at main · Aihong-Sun/Fuzzy_time_FJSP_Instance (github.com)

4 算法

使用普通GA+精英保留策略（种群个数：100，迭代次数：100，交叉率：0.8，变异率：0.05，Elite个数：10）对算例进行了测试.

注：本文的交叉变异设置较为随意且未加任意局部搜索等，效果有差距属于正常，

4.1 文献【2】中算例验证

        文献2中对自己生成的算例的测试结果如下：

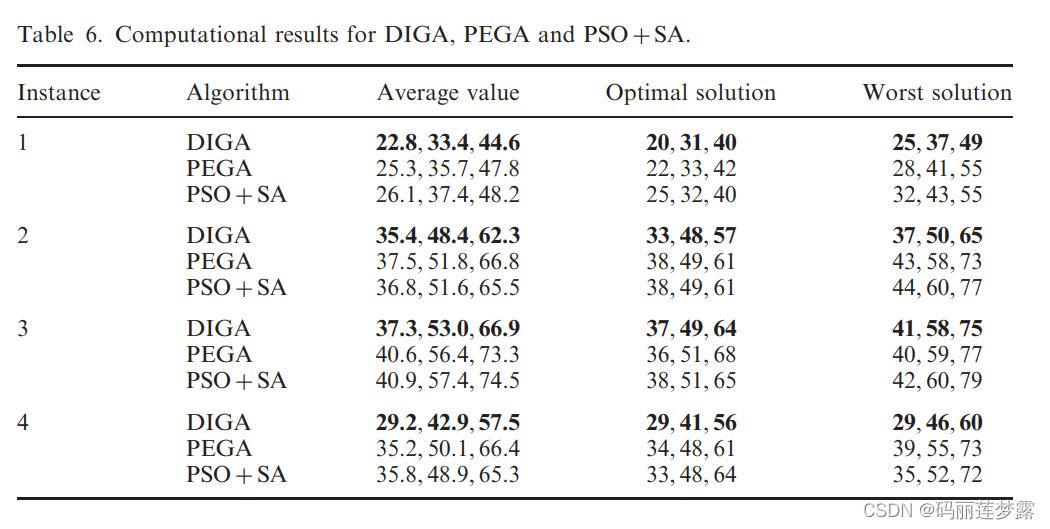
        本文用普通GA的测试10次得到的效果如下 ：

Instance	Best	worst	CPU(s)
1	[21,32,44]	[25,35,49]	4.19
2	[35,50,62]	[36,50,67]	4.06
3	[40,55,69]	[38,55,74]	5.53
4	[28,40,57]	[30,43,62]	5.52

参考文献：

[1]Sakawa M, Kubota R. Fuzzy programming for multiobjective job shop scheduling with fuzzy processing time and fuzzy duedate through genetic algorithms[J]. European Journal of Operational Research, 2000, 120(2): 393-407.

[2]Lei D M. A genetic algorithm for flexible job shop scheduling with fuzzy processing time[J]. International Journal of Production Research, 2010, 48(10): 2995-3013.

[3]Xu,,Ye,Wang,,Ling,Wang,,Sheng-yao,Liu,,& Min.(2015).An effective teaching-learning-based optimization algorithmfor the flexible job-shop scheduling problem with fuzzy processing time.NEUROCOMPUTING,148,260-268.

[4]郭钧,钟精诚,杜百岗等.考虑模糊作业时间的再制造加工车间多目标调度方法[J].控制与决策,2020,35(6):1497-1504.

4 部分代码展示

'''
by: Aihong-Sun
use for: Job describe
'''
from Flexible_Job_Shop.Job import Job
from Flexible_Job_Shop.Machine import Machine
from Fuzzy_Shop_Floor.Fuzzy_time_operator import *

class Job_fuzzy(Job):
    def __init__(self,idx,processing_machine,processing_time):
        super(Job_fuzzy, self).__init__(idx,processing_machine,processing_time)
        self.end=[0,0,0]

class Machine_fuzzy(Machine):
    def __init__(self, idx):
        super(Machine_fuzzy, self).__init__(idx)

    def update(self,s,e,Job):
        self.start.append(s)
        self.start.sort(key=lambda u:u[1])
        self.end.append(e)
        self.end.sort(key=lambda u:u[1])
        idx=self.start.index(s)
        self._on.insert(idx,Job)

    def find_start(self,s,o_pt):
        if self.end==[]: return s
        else:
            if Measure(s,self.end[-1]):return s
            else:
                o_s=self.end[-1]
                l = len(self.end) - 2
                while l>=0:
                    if Measure(add(s,o_pt),self.start[l+1]):
                        break
                    if Measure(self.end[l],s) and Measure(self.start[l+1],add(self.end[l],o_pt)):
                        o_s=self.end[l]
                    elif  Measure(s,self.end[l]) and Measure(self.start[l+1],add(s,o_pt)):
                        o_s=s
                    l-=1
                return o_s

'''
by: Aihong-Sun
use for: Job shop describe
'''
from Fuzzy_Shop_Floor.fuzzy_SF_Item import Job_fuzzy as Job
from Fuzzy_Shop_Floor.fuzzy_SF_Item import Machine_fuzzy as Machine
from Fuzzy_Shop_Floor.Fuzzy_time_operator import *

class Job_shop:
    def __init__(self,args):
        self.n= args.n
        self.m=args.m
        self.O_num=args.O_num
        self.PM = args.Processing_Machine
        self.PT = args.Processing_Time

    def reset(self):
        self.C_end=[0,0,0]
        self.C_max = 0
        self.Jobs=[]
        for i in range(self.n):
            Ji=Job(i,self.PM[i],self.PT[i])
            self.Jobs.append(Ji)
        self.Machines=[]
        for j in range(self.m):
            Mi=Machine(j)
            self.Machines.append(Mi)

    #Xu,,Ye,Wang,,Ling,Wang,,Sheng-yao,Liu,,& Min.(2015).An effective teaching-learning-based optimization algorithm
    # for the flexible job-shop scheduling problem with fuzzy processing time.NEUROCOMPUTING,148,260-268.
    def decode(self,Job,Machine):
        Ji=self.Jobs[Job]
        o_pt, s,M_idx = Ji.get_next_info(Machine)
        Mi=self.Machines[M_idx-1]
        start=Mi.find_start(s,o_pt)
        end=add(start,o_pt)
        Ji.update(end)
        Mi.update(start,end,[Ji.idx,Ji.cur_op])
        if Measure(end,self.C_end):
            self.C_end=end
            self.C_max=TFN_value(end)

'''
operation of fuzzy time
Contain function: add(X,Y);Measure(X,Y);
'''

def add(X,Y):
    return [X[_]+Y[_] for _ in range(3)]

def TFN_value(X):
    return (X[0] + 2 * X[1] + X[2]) / 4

def Measure(X,Y):
    F_X=TFN_value(X)
    F_Y=TFN_value(Y)
    if F_X!=F_Y:
        if F_X>F_Y:return True
        else:return False
    else:
        if X[1]!=Y[1]:
            if X[1]>Y[1]:return True
            else:return False
        else:
            if X[2]-X[0]>Y[2]-Y[0]:return True
            else:return False