正态分布的分布函数是啥?

Posted 2023-05-09

正态分布（Normal distribution），也称“常态分布”，又名高斯分布（Gaussian distribution），最早由棣莫弗（Abraham de Moivre）在求二项分布的渐近公式中得到。

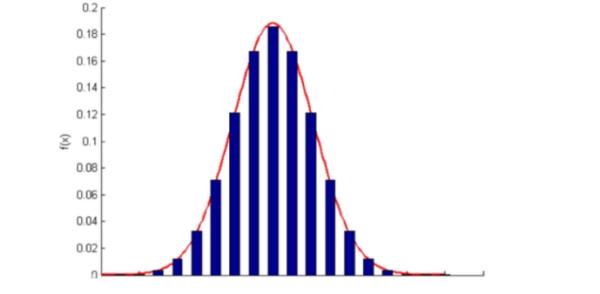正态曲线呈钟型，两头低，中间高，左右对称因其曲线呈钟形，因此人们又经常称之为钟形曲线。若随机变量X服从一个数学期望为μ、方差为σ2的正态分布，记为N(μ，σ2)。其概率密度函数为正态分布的期望值μ决定了其位置，其标准差σ决定了分布的幅度。当μ=0,σ=1时的正态分布是标准正态分布。

扩展知识：

正态分布概念是由法国数学家棣莫弗（Abraham de Moivre）于1733年首次提出的，后由德国数学家Gauss率先将其应用于天文学研究，故正态分布又叫高斯分布，高斯这项工作对后世的影响极大，他使正态分布同时有了“高斯分布”的名称，后世之所以多将最小二乘法的发明权归之于他，也是出于这一工作。

但德国10马克的印有高斯头像的钞票，其上还印有正态分布的密度曲线。这传达了一种想法：在高斯的一切科学贡献中，其对人类文明影响最大者，就是这一项。在高斯刚作出这个发现之初，也许人们还只能从其理论的简化上来评价其优越性，其全部影响还不能充分看出来。这要到20世纪正态小样本理论充分发展起来以后。

其实，他提出的形式有相当大的局限性：海根把误差设想成个数很多的、独立同分布的“元误差” 之和，每只取两值，其概率都是1/2，由此出发，按棣莫弗的中心极限定理，立即就得出误差（近似地）服从正态分布。拉普拉斯所指出的这一点有重大的意义，在于他给误差的正态理论一个更自然合理、更令人信服的解释。

因为，高斯的说法有一点循环论证的气味：由于算术平均是优良的，推出误差必须服从正态分布；反过来，由后一结论又推出算术平均及最小二乘估计的优良性，故必须认定这二者之一为出发点。但算术平均到底并没有自行成立的理由，以它作为理论中一个预设的出发点，终觉有其不足之处。拉普拉斯的理论把这断裂的一环连接起来，使之成为一个和谐的整体，实有着极重大的意义。

以上内容参考百度百科：正态分布

参考技术A

正态分布（Normal distribution），也称“常态分布”，又名高斯分布（Gaussian distribution），最早由棣莫弗（Abraham de Moivre）在求二项分布的渐近公式中得到。C.F.高斯在研究测量误差时从另一个角度导出了它。P.S.拉普拉斯和高斯研究了它的性质。是一个在数学、物理及工程等领域都非常重要的概率分布，在统计学的许多方面有着重大的影响力。

正态曲线呈钟型，两头低，中间高，左右对称因其曲线呈钟形，因此人们又经常称之为钟形曲线。若随机变量X服从一个数学期望为μ、方差为σ2的正态分布，记为N(μ，σ2)。其概率密度函数为正态分布的期望值μ决定了其位置，其标准差σ决定了分布的幅度。当μ = 0,σ = 1时的正态分布是标准正态分布。

学习共享内存、分布式内存和/或 GPU 编程的典型问题和解决方案是啥？

【中文标题】学习共享内存、分布式内存和/或 GPU 编程的典型问题和解决方案是啥？

【英文标题】：What is an exemplar problem and solution for learning shared memory, distributed memory, and/or GPU programming?学习共享内存、分布式内存和/或 GPU 编程的典型问题和解决方案是什么？

【发布时间】：2011-08-10 17:16:18

【问题描述】：

我们正在寻找可在任何或所有共享内存、分布式内存和 GPGPU 架构上运行的示例问题和代码。我们使用的参考平台是 LittleFe (littlefe.net)，这是一个开放式设计、低成本的教育集群，目前有六个双核 CPU，每个 CPU 都有一个 nVidia 芯片组。

这些问题和解决方案将有助于向任何新手教授并行性，提供工作示例和机会来卷起袖子和代码。 *** 专家有很好的洞察力，并且可能有一些收藏夹。

计算曲线下的面积很有趣，简单易懂，但肯定有一些同样容易表达，并且充满了练习和学习的机会。

使用一种以上内存架构的混合示例是最可取的，并且反映了并行编程的趋势似乎在哪里。

在 LittleFe 上，我们主要使用三个应用程序。第一个是对飞镖上最佳目标的分析，该飞镖高度并行且通信开销很小。第二个是康威的生命游戏，这是一个典型的共享边界条件的问题。它具有适度的通信开销。第三个是星系形成的 n 体模型，需要大量的通信开销。

【参考方案1】：

CUDA programming guide(PDF) 包含对 GPU 上矩阵乘法实现的详细分析。这似乎是学习 GPU 编程的主要“hello world”示例。

此外，CUDE SDK 包含数十个其他解释清楚的 CUDA 和 OpenCL 中的 GPU 编程示例。我最喜欢的是碰撞球的例子。 （数千个球实时碰撞的演示）

【讨论】：

Sweet，自从《和米奇一起唱》以来，人们就喜欢弹跳球，也许可以修改它来展示理想气体定律。

【参考方案2】：

我最喜欢的两个是数值整数和寻找素数。首先，我们在函数 f(x) = 4.0 / (1.0 + x*x) 上编写中点矩形规则。函数在 0 和 1 之间的积分给出了常数 pi 的近似值，这使得检查答案的正确性变得容易。并行度跨越积分范围（计算矩形的面积）。

对于第二个，我们输入一个整数范围，然后识别并保存该范围内的素数。我们使用所有可能的因素对值进行强力划分；如果发现任何除数不是 1 或数字，则该值是合数。如果找到素数，则对其进行计数并存储在共享数组中。并行性正在划分范围，因为 N 的素数测试独立于 M 测试。在线程之间共享素数存储或收集分布式部分答案需要一些技巧。

这些都是非常基本且易于解决的问题，这使学生可以专注于并行实现，而不是过多地关注所涉及的计算。

【讨论】：

谢谢克莱。我知道我最喜欢的线猴会有一些很棒的建议。

Clay、Andrew Fitz Gibbon 和我在 Fitz 和我任教的 Petascale 研究所结束时相遇，从事 ACM 技术包 2 的并行编程工作。我使用了一个直接与单位圆方程相关的变体，x^2 + y^2 = 1，求解 y 得到 y=sqrt(1-x^2)。将其下方的面积从 -1 到 1 得出半圆的面积，即 pi/2。我在 Petascale 研究所用它来教授 mpi 点对点通信，也作为伯克利 Map-Reduce 主题的一个例子。其他人扩展了我的此代码的串行版本来教授 OpenMP 和 Cuda。

【参考方案3】：

其中一个更复杂但更简单的示例问题是 BLAS 例程 sgemm 或 dgemm (C = alpha * A x B + beta * C)，其中 A、B、C 是有效大小的矩阵，而 alpha 和 beta 是标量。类型可以是单精度浮点 (sgemm) 或双精度浮点 (dgemm)。

在不同的平台和架构上实现这个简单的例程，让我们了解了一些关于功能和工作原理的见解。有关 BLAS 和 ?gemm 例程的更多详细信息，请查看http://www.netlib.org/blas。

您只需要注意，对于 GPU 上的双精度实现，GPU 需要具有双精度功能。

【讨论】：

这是一个很好的建议。谢谢。它也自然而然地引发了对 BLAS 和其他数值库的调查/讨论。第二个出发点是讨论误差，从单精度到双精度并获得相同的结果并不足以验证算法的数值稳定性