复化梯形公式和复化Simpson公式的python实现

Posted 2022-11-25 小龙呀

复化求积的思想：
       将区间[a，b]分作n等分，步长h = (b-a) / n，等分点x(k) = a + kh，k = 0,1,2,3,…,n，先在每个子区间[x(k)，x(k+1)]上采用低阶的数值求积公式求得近似积分值I(k)，再将它们累加并以和作为积分I的近似值。

用复化梯形公式和复化Simpson公式计算：
$$I={\int }_0^{\pi }{e}^{x}cosxdx$$
精确值是：I = -12.0703463164

（1）复化梯形公式：

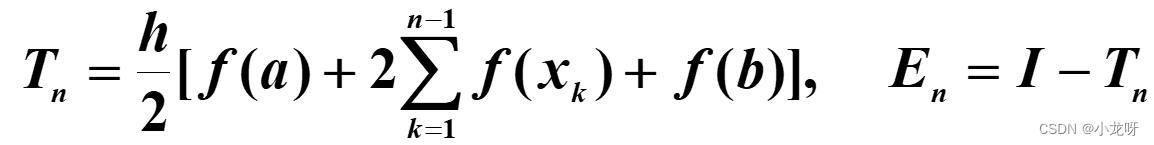
python代码：

运行结果：

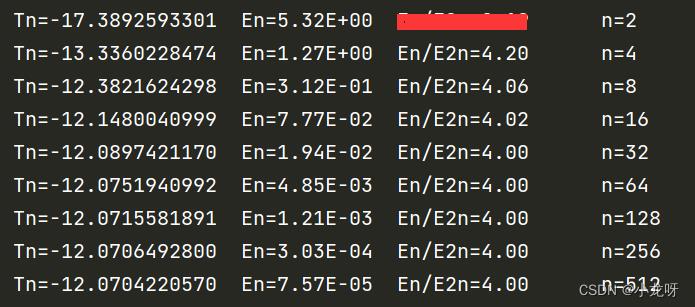
结论：
       当n加倍（步长h减半）时，误差E(n)按因子4递减，误差确是O(h^2)；当n增大时，复化梯形公式的误差越来越小，近似解也越来越收敛于精确解；但是，当n相对较小时，求解效果并不是太好，误差相对较大。

（2）复化Simpson公式：

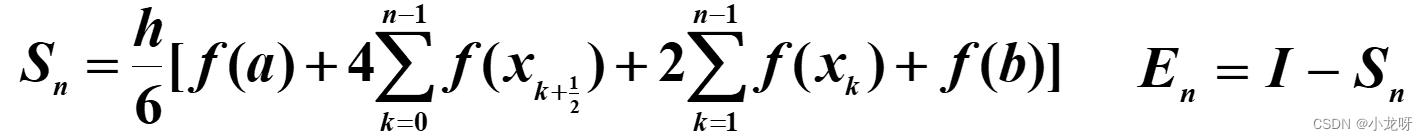
python代码：

运行结果：

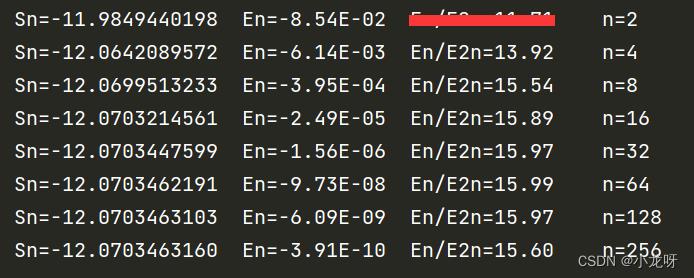
结论：
       当n加倍（步长h减半）时，误差E(n)按因子16递减，误差确是O(h^4)；当n增大时，复化Simpson公式的误差越来越小，近似解也越来越收敛于精确解；复化Simpson公式总体上近似效果较好，要比复化梯形公式优越的多。