由浅入深讲解哈夫曼树

Posted 2022-02-05 一直会努力的波吉

由浅入深讲解哈夫曼树

学前须知

哈夫曼树相关的名词

路径：在一棵树中，一个结点到另一个结点之间的通路，称为路径。下图中，从根结点到结点 a 之间的通路就是一条路径

路径长度：在一条路径中，每经过一个结点，路径长度都要加 1 。例如在一棵树中，规定根结点所在层数为1层，那么从根结点到第 i 层结点的路径长度为 i - 1 。图中从根结点到结点 c 的路径长度为 3

结点的权：给每一个结点赋予一个新的数值，被称为这个结点的权。例如，图中结点 a 的权为 7，结点的权为 5

结点的带权路径长度：指的是从根结点到该结点之间的路径长度与该结点的权的乘积。例如，图中结点 b 的带权路径长度为 2 * 5 = 10

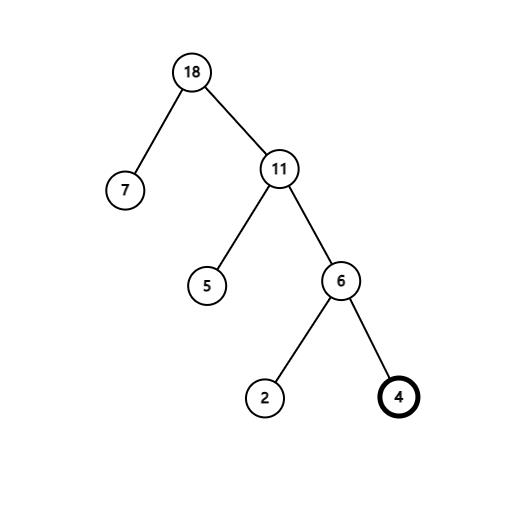
树的带权路径长度为树中所有叶子结点的带权路径长度之和。通常记作 “WPL” 。例如图中所示的这颗树的带权路径长度为：WPL = 7 * 1 + 5 * 2 + 2 * 3 + 4 * 3

什么是哈夫曼树

当用 n 个结点（都做叶子结点且都有各自的权值）试图构建一棵树时，如果构建的这棵树的带权路径长度最小，称这棵树为“最优二叉树”，有时也叫"哈夫曼树"。

构建哈夫曼树的过程是贪婪策略的体现，权重越大的结点离树根越近。在上图中，因为结点 a 的权值最大，所以应当作为根结点的孩子结点。

构建哈夫曼树

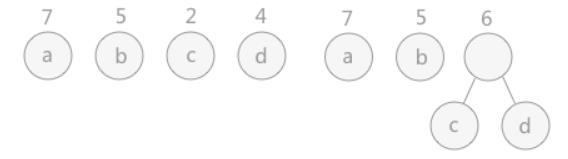
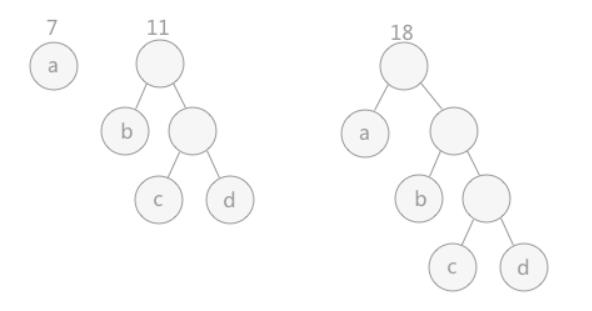
对于给定的有各自权值的 n 个结点，构建哈夫曼树有一个行之有效的办法：

1. 在 n 个权值中选出两个最小的权值，对应的两个结点组成一个新的二叉树，且新二叉树的根结点的权值为左右孩子权值的和；
2. 在原有的 n 个权值中删除那两个最小的权值，同时将新的权值加入到 n–2 个权值的行列中，以此类推；
3. 重复 1 和 2 ，直到所以的结点构建成了一棵二叉树为止，这棵树就是哈夫曼树。