数据结构和算法超详细，超多图解，赫夫曼树详解
Posted Linux猿
tags:
篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了数据结构和算法超详细，超多图解，赫夫曼树详解相关的知识，希望对你有一定的参考价值。
🎈 作者：Linux猿
🎈 简介：CSDN博客专家🏆，华为云享专家🏆，数据结构和算法、C/C++、面试、刷题、Linux尽管咨询我，关注我，有问题私聊！
🎈 关注专栏：动图讲解数据结构和算法（优质好文持续更新中……）🚀
🎈 欢迎小伙伴们点赞👍、收藏⭐、留言💬
目录
赫夫曼树是在考试、考研、面试中经常提到的一个知识点，下面就让我们一块来看下赫夫曼树及其应用吧！
🔶🔶🔶🔶🔶 我是分割线 🔶🔶🔶🔶🔶
🍓一、什么是赫夫曼树 ？
在说赫夫曼树之前，一定要先了解一个概念“带权路径长度”，简称 WPL。WPL 已在文章【数据结构和算法】超详细，超多图解，树的各种概念汇总 中进行了介绍。
赫夫曼树是带权路径长度（WPL） 最小的二叉树，也称作最优二叉树、哈夫曼树、霍夫曼树。
该算法是由 Huffman 在攻读博士学位期间开发的算法。
🔶🔶🔶🔶🔶 我是分割线 🔶🔶🔶🔶🔶
🍓二、赫夫曼树的特性
（1）赫夫曼树是一棵二叉树；
（2）赫夫曼树中结点的度为 0 或 2，即没有度为 1 的结点；
🔶🔶🔶🔶🔶 我是分割线 🔶🔶🔶🔶🔶
🍓三、赫夫曼树的构造过程
✨3.1 算法思路
假设给定 n 个权值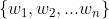 
要求构造一棵具有 n 个叶子结点的二叉树，每个叶子结点的权值为 
，求带权路径最小的二叉树。
构造赫夫曼树的算法步骤如下所示：
（1）根据给定的 n 个权值，构造一个二叉树的集合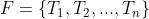 
，初始时，
为单个结点的子树，权值为 ，左右子树为空；
（2）在二叉树的集合中选择权值最小的两棵子树，两个子树分别作为新子树的左右子树，添加一个新结点作为两个子树的父节点，新结点的权值为左右子树根结点之和；
（3）删除原集合中步骤（2）选中的两棵子树，将新合并的子树加入到集合 F 中；
（4）重复步骤 （2）~（3），直到集合中只有一颗子树为止；
（5）此时的二叉树称为赫夫曼树。
✨3.2 实例演示
假设给定 7 个权值 {10, 8, 9, 15, 23, 7, 16} ，要求构造一棵具有 7 个叶子结点的二叉树，叶子结点的权值依次为{10, 8, 9, 15, 23, 7, 16}，求带权路径最小的二叉树。
初始时，集合 F 中子树根结点的权值为 {10, 8, 9, 15, 23, 7, 16}，如下图所示：
构造赫夫曼树的步骤如下所示：
（1）选择集合 F 中子树根结点最小的两个结点，选择 8 和 7，将其组成一个新的子树，如下所示：
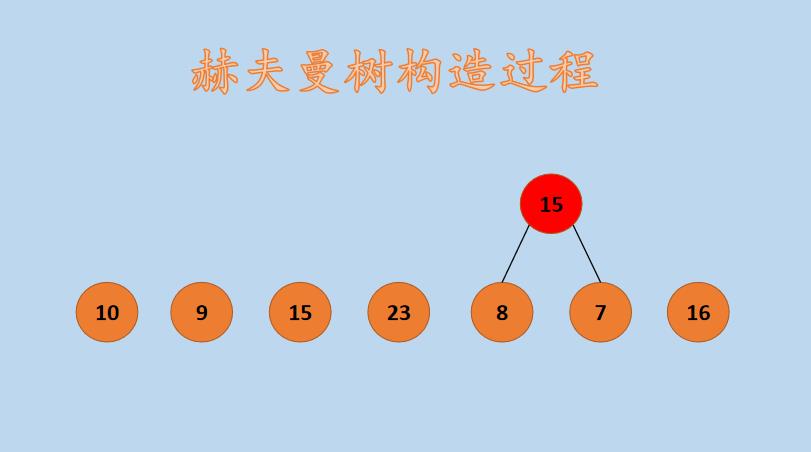
（2）此时，集合 F 中子树根结点的权值为 {10，9，15，23，15，16}，其中，第二个 15 为 8 和 7 合并后新的根结点的权值。再次选择两个最小权值的子树，选择 10 和 9，将其组成一个新的子树，如下所示：
（3）此时，集合 F 中子树根结点的权值为 {19,15,23,15,16}，19 为 10 和 9 合并后新的值。再次选择两个最小权值的子树，选择 15 和 15，将其组成一个新的子树，如下所示：
（4）此时，集合 F 中子树根结点的权值为 {19,23,30,16}，30 为 15 和 15 合并后的新值。再次选择两个最小权值的子树，选择19和16，将其组成一个新的子树，如下所示：
（5） 此时，集合 F 中子树根结点的权值为 {23,30,35}，35 为 19 和 16 合并后的新值。再次选择两个最小权值的子树，选择23 和 30，将其组成一个新的子树，如下所示：
（6）此时，集合 F 中子树根结点的权值为 {53,35}，其中，53 为 23 和 30 合并后的新值。再次选择两个最小权值的子树，选择 53 和 35，将其组成一个新的子树，如下所示：
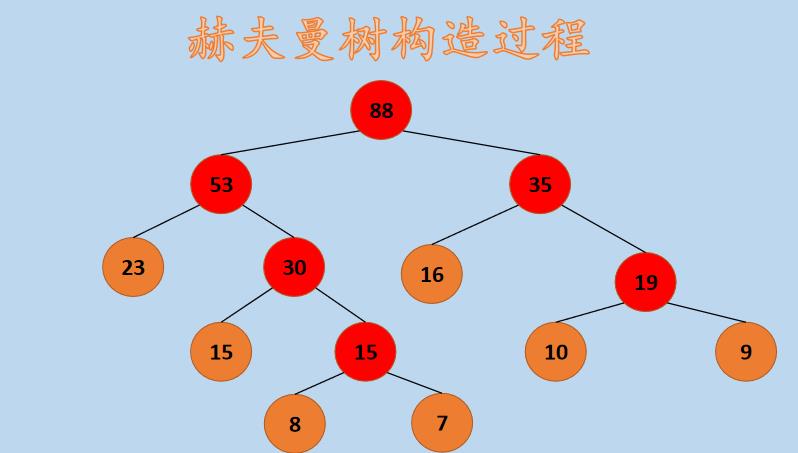
（7）此时，集合 F 中只有一颗树，这棵树便是最优二叉树/赫夫曼树。
🔶🔶🔶🔶🔶 我是分割线 🔶🔶🔶🔶🔶
🍓四、应用-赫夫曼编码
✨4.1 题目描述
已知存在字符集 {A，B，C，D，E，F} ，各字母出现的频率依次为 5，7，12，2，18，9。求哈夫曼编码。
✨4.2 算法思路
本题是赫夫曼编码的应用，字母出现的频率是字符的权重，将其作为叶子结点，计算赫夫曼树，然后进行赫夫曼编码即可。
✨4.3 动图解析
下面来看一下动图建立赫夫曼树的过程，如下所示：
在上图中，紫色表示为构造赫夫曼树新添加的点，建立完赫夫曼树后，本文按照左 0 右 1 的策略编码，如下所示：
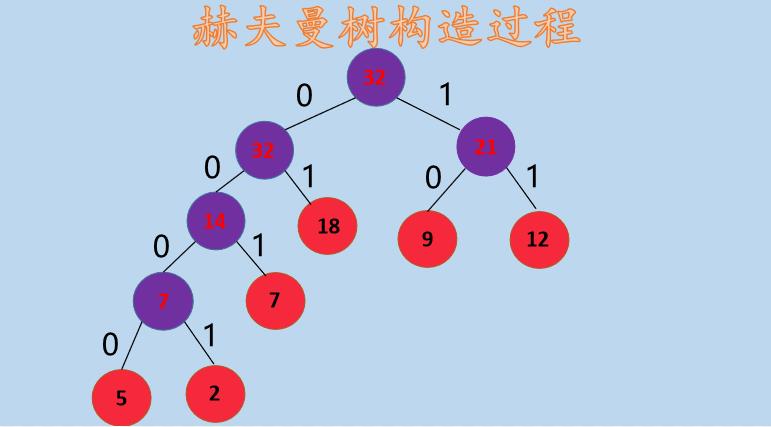
经过上图的编码后，各字符的编码如下所示：
A （权值为 5 的叶子结点）的编码为：0000
B（权值为 7 的叶子结点）的编码为：001
C（权值为 12 的叶子结点）的编码为：11
D（权值为 2 的叶子结点）的编码为：0001
E（权值为 18 的叶子结点）的编码为：01
F（权值为 9 的叶子结点）的编码为：10
赫夫曼编码是一种无前缀编码，什么是无前缀呢？
无前缀是指字符的编码相互之间没有哪个是另一个的前缀（例如：有两个字符编码分别为 0011 和 001，那么 001 就是 0011 的前缀），可以看到，上面的例子中，经过编码后，A、B、C、D、E、F 都是无前缀编码，相互之间没有一个是另一个的前缀。
🔶🔶🔶🔶🔶 我是分割线 🔶🔶🔶🔶🔶
🍓五、赫夫曼树题目
下面列出了两道练习题，理解后一定要联系哦！
（1）北大OJ Entropy
题解后续会更新到公众号中，记得关注文章末尾公众号！
🔶🔶🔶🔶🔶 我是分割线 🔶🔶🔶🔶🔶
🍓六、总结
在学习赫夫曼树时，首先要掌握赫夫曼树的构造过程，在此基础上掌握赫夫曼编码的原理，最后做题巩固即可！
如果感觉对你有帮助，点赞👍、收藏⭐、留言💬支持下吧！
关注下方👇👇👇👇👇公众号👇👇👇👇👇，获取更多优质好文🤞（比心）！
以上是关于数据结构和算法超详细，超多图解，赫夫曼树详解的主要内容，如果未能解决你的问题，请参考以下文章