数据结构 Java 版二叉树的实现（超多图超详解）

Posted 谢谢你，泰罗！

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了数据结构 Java 版二叉树的实现（超多图超详解）相关的知识，希望对你有一定的参考价值。

文章目录

1. 树型结构

1.1 概念

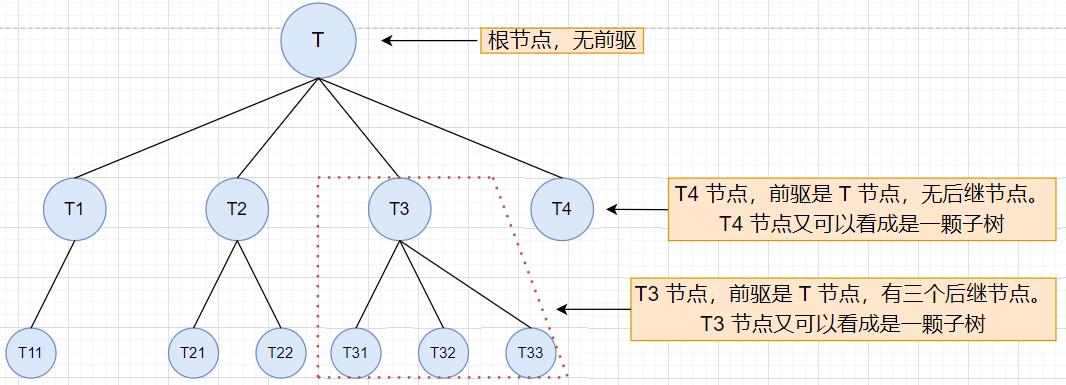
树：是一种非线性的数据结构，它是由 n（n>=0）个有限节点组成的一个具有层次关系的集合。把它叫做树是因为它看起来像一颗倒挂的树，它是根朝上，叶朝下。

特点：

  • 有一个特殊的节点，称为根节点，根节点没有前驱节点

  • 除根节点外，其余节点被分成 M（M>0）个互不相交的集合（T1、T2、…、Tm），其中每一个集合 Ti（1<=i<=m）又是一颗与树类似的子树。每颗子树的根节点有且只有一个前驱，可以有0个或多个后继

  • 一颗 N 个节点的树有 N-1 条边

  • 树是递归定义的

注意：

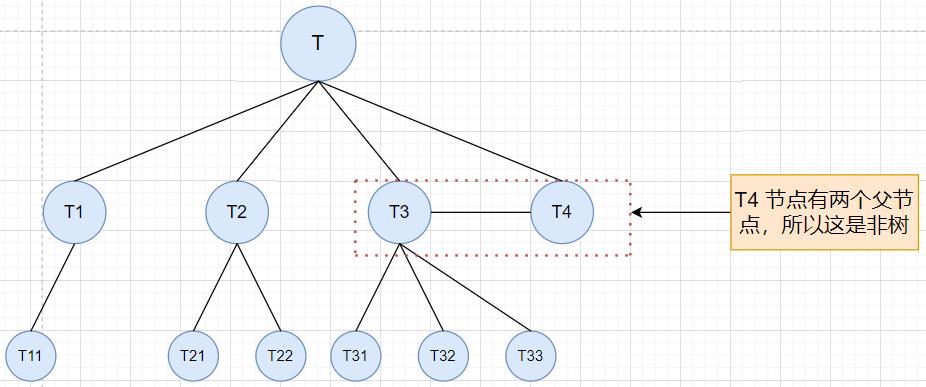
子树是不相交的，即除每个节点有且仅有一个父节点。而下面的几种情况都是非树

  • 情况一：
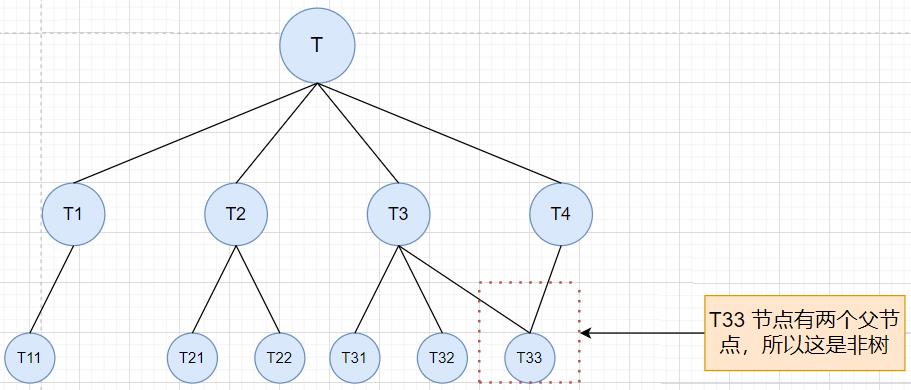
  • 情况二：
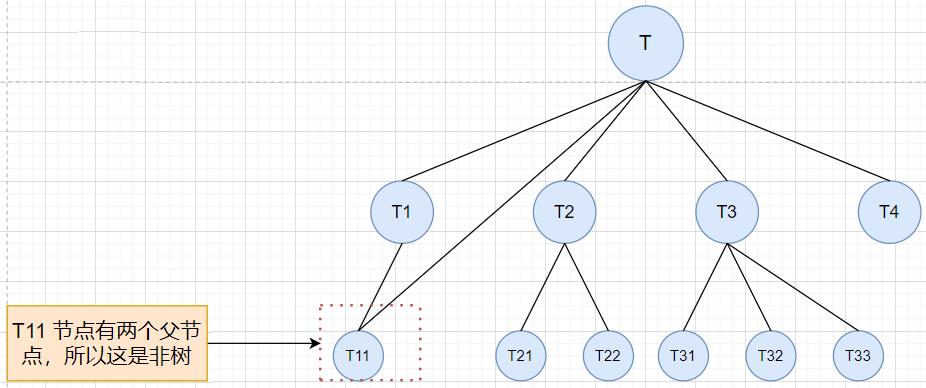
  • 情况三：

1.2 要掌握的知识点

大家可以配合此图，食用以下关于树的知识点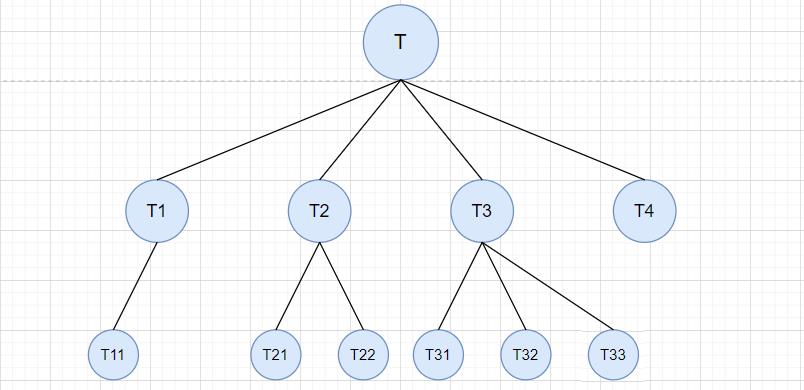

  • 节点的度： 一个节点含有的子树的个数称为该节点的度。如上图，T 节点的度为4
  • 树的度： 一颗树中，最大的节点的度称为树的度。如上图，该树的度为4
  • 叶子节点或终端节点： 度为0的节点称为叶子节点。如上图，T4、T11、T21、T22、T31、T32、T33为叶子节点
  • 双亲节点或父节点： 若一个节点含有子节点，则这个节点称为其子节点的父节点。如上图，T 节点是 T4 节点的父节点
  • 孩子节点或子节点： 一个节点含有的子树的根节点称为该节点的子节点。如上图，T4 节点是 T 节点的子节点
  • 根节点： 一颗树中，没有双亲节点的节点称为根节点。如上图，T 节点为根节点
  • 节点的层次： 从根开始定义，根为第1层，根的子节点为第二层，以此类推。如上图，该树有3层
  • 节点的深度： 某节点层次是第几层，则它的深度是多少。如上图，T 节点深度为1，T1 节点深度为2
  • 树的高度： 树中节点的最大层次。如上图，树的高度为3
  • 非终端节点或分支节点： 度不为0的节点。如上图，T、T1、T2、T3 为分支节点
  • 兄弟节点： 父亲节点相同的节点互称为兄弟节点。如上图，T1、T2、T3、T4 互称为兄弟节点
  • 堂兄弟节点： 双亲在同一层次的节点互称为堂兄弟节点。如上图，T11、T21 互称为堂兄弟节点
  • 节点的祖先： 从根节点到该节点所经过分支上的所有节点都称为该节点的祖先。如上图，T、T1 节点都为 T11 节点的祖先
  • 子孙： 以某节点为根的子树中，任意节点都称为该节点的子孙。如上图，该树中除 T 节点其它节点都是 T 节点的子孙
  • 森林： 由 m（m>=0）棵互不相交的树的集合称为森林。

1.3 树的存储形式

树是一种非线性的数据结构，所以存储数据相较于线性结构其实要麻烦很多。常用的方法有：双亲表示法、孩子表示法、孩子兄弟表示法等等。这里我们主要介绍最常用的孩子兄弟表示法。

孩子兄弟表示法的代码表现形式：

class Node{
    int val;			// 树中存储的数据
    Node firstChild;	// 第一个孩子的引用
    Node nextBrother;	// 下一个兄弟的引用
}

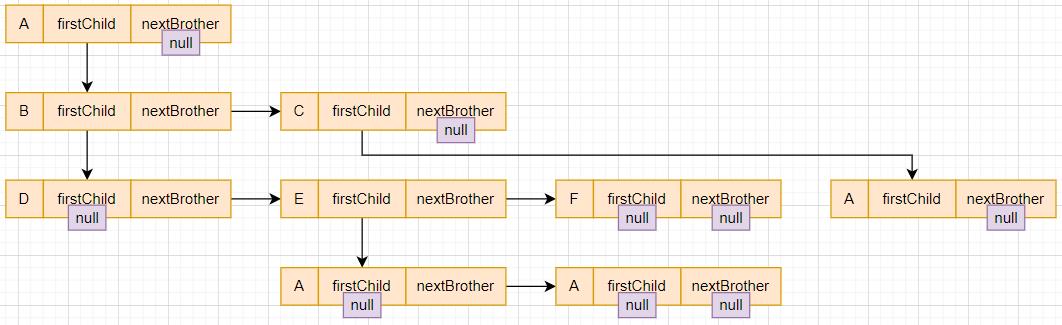
我们可以引用下面这棵树的图片，对它进行解析来理解上述代码的意思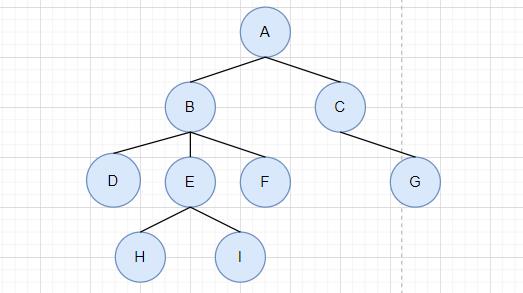

解析： 每一个节点都有一个第一个孩子结点和下一个兄弟结点，通过这两个结点，就可以将这棵树的所有结点联系起来。使得我们可以遍历，并将数据存储。

1.4 树的应用

其实我们电脑的文件系统管理和树的结构很相似，尤其是有着一切皆文件之称的 linux 系统。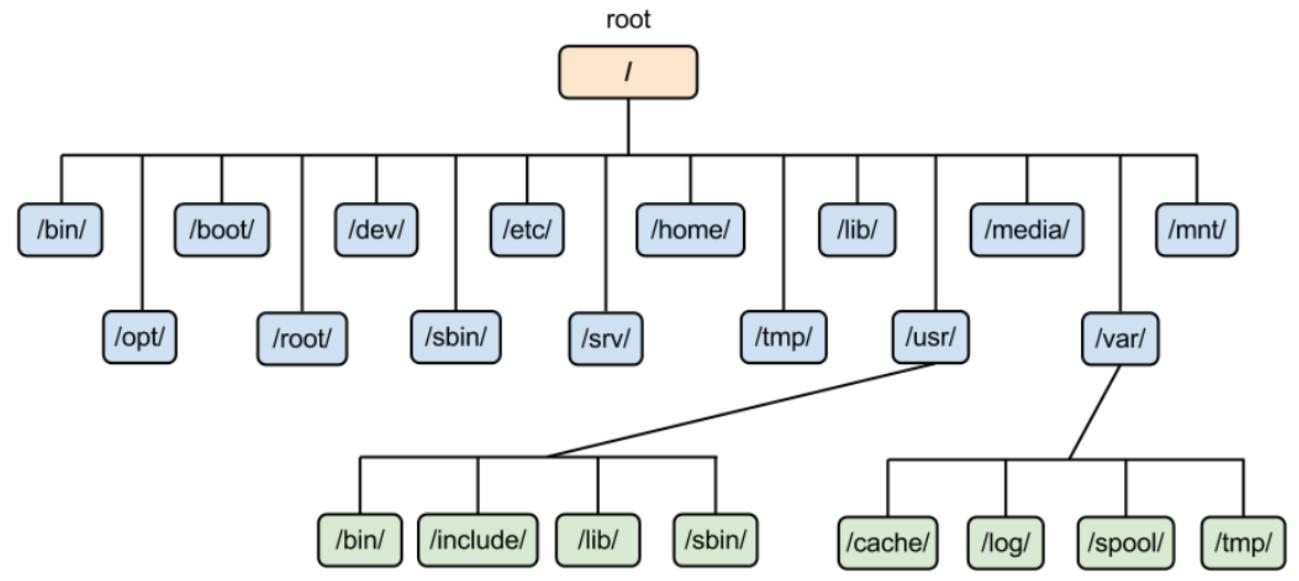

因此我们可以使用树的知识，去构建一个系统的目录和文件。

2. 二叉树

2.1 概念

二叉树：是 n 个有限元素的集合，该集合或者为空，或者是由一个根节点加上两棵不相交的，被分别称为左子树和右子树的二叉树组成。

特点：

  • 当集合为空时，该二叉树称为空二叉树。
  • 在二叉树中，一个元素也称为一个结点。
  • 每个结点最多有两棵子树，即二叉树不存在度大于2的结点。
  • 二叉树的子树有左右之分，其次子树的次序不能颠倒，因此二叉树是有序树。

2.2 二叉树的基本形态

一般二叉树都是由以下四种形态的二叉树组合形成的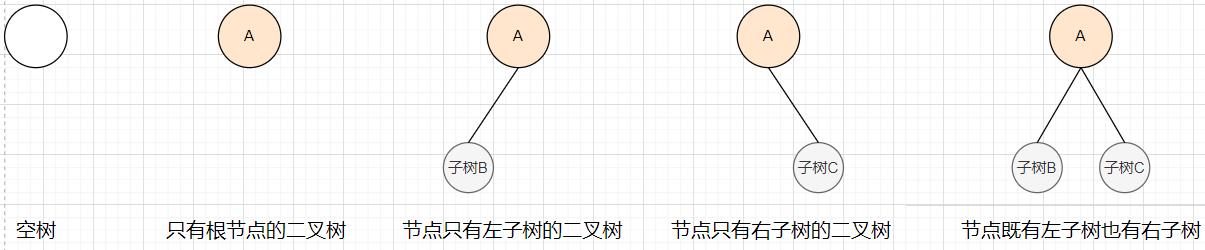

注意：

子树也必须是二叉树才能满足该树整体是一个二叉树

2.3 两种特殊的二叉树

2.3.1 满二叉树

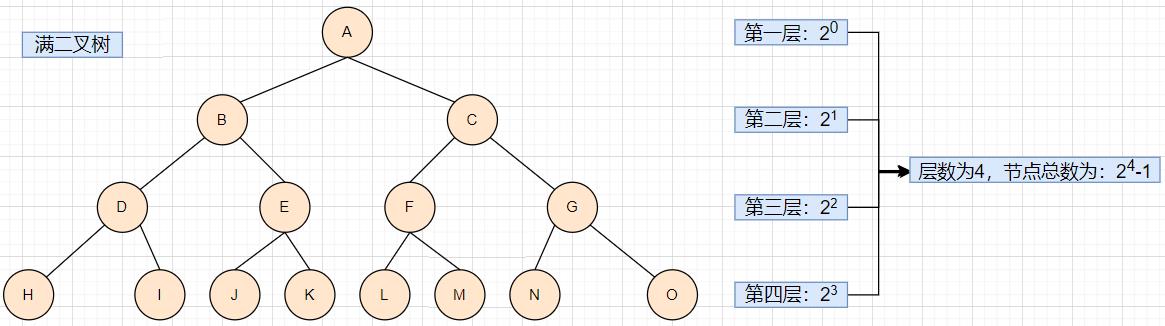
满二叉树： 一个二叉树，如果每一层的节点数都达到最大值，则这个二叉树就是满二叉树。

性质： 如果一个二叉树的层数是k，且节点数是 2k-1，则它就是满二叉树。

2.3.2 完全二叉树

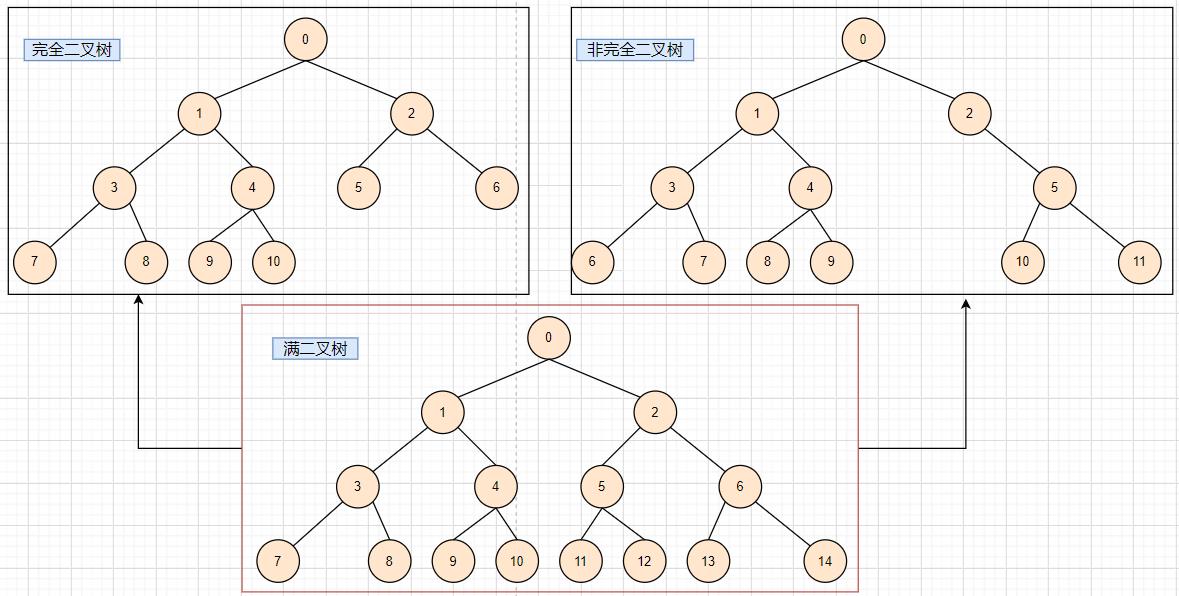
完全二叉树： 完全二叉树是效率很高的数据结构，它是由满二叉树引申出来的。它的叶子节点只会出现在最后2层，且最后一层的叶子节点都靠左对齐。 （满二叉树是一种特殊的完全二叉树）

2.4 二叉树的性质

  • 若规定根节点的层数为1，则一棵非空二叉树的第 i 层上最多有 2i-1（i>0）个节点
  • 若规定只有根节点的二叉树的深度为1，则深度为 k 的二叉树的最大节点数是 2k-1（k>=0）
  • 对任何一棵二叉树，如果其叶子节点个数为 m，度为2的非叶子节点个数为 n，则有 m=n+1
  • 具有 n 个节点的完全二叉树的深度为 log2(n+1) 向上取整
  • 对于具有 n 个节点的完全二叉树，如果按照从上至下、从左至右的顺序对所有节点从0开始编号，则对序号为 i 的节点有：
    • 若 i>0，双亲序号为：(i-1)/2
    • 若 i=0，i 为根节点编号，无双亲节点
    • 若 2i+1<n，左孩子序号为：2i+1，否则没有左孩子
    • 若 2i+2<n，右孩子序号为：2i+2，否则没有右孩子

练习题：

假设一棵完全二叉树中总共有1000个节点，则该二叉树中有____个叶子节点，____个非叶子节点，____个节点只有左孩子，____个节点只有右孩子。

答案：

500、500、1、0

解析：

  • 由于这是一个完全二叉树，所以不可能出现只有右孩子的节点，故最后一空为0
  • 通过节点个数1000，可以推导出该树的深度为10
  • 第10层节点数可以通过总节点数减去前9层节点数得到，为1000-511=489
  • 叶子节点数=第10层的节点数+第九层度为0的节点数，而通过第10层的节点数可以知道他们的父节点有489/2+1=245
  • 由于这是一个完全二叉树，所以第9层的节点肯定是满的，易得第9层节点数为256，而去除第九层度不为0的节点数，得到第九层叶子节点有256-245=11
  • 故叶子节点数为489+11=500，非叶子节点数为1000-500=500
  • 而完全二叉树的节点只有左子树的结果有1或0，通过第十层的节点数489为偶数，我们知道肯定有一个父节点只有一个孩子节点，即只有左子树的节点为1

2.5 二叉树的存储

二叉树的存储结构分为：顺序存储（在堆中介绍）和类似于链表的链式存储

二叉树的链式存储是通过一个一个的节点引用起来的，表示方法有：孩子表示法和孩子双亲表示法

孩子表示法：

class Node{
    int val;		// 数值域
    Node left;		// 左孩子的引用，常常代表以左孩子为根的整棵树
    Node right;		// 右孩子的引用，常常代表以右孩子为根的整棵树
}

孩子双亲表示法：

class Node{
    int val;		// 数值域
    Node left;		// 左孩子的引用，常常代表以左孩子为根的整棵树
    Node right;		// 右孩子的引用，常常代表以右孩子为根的整棵树
    Node parent;	// 当前节点的根节点
}

2.6 二叉树的基本操作

2.6.1 二叉树的前、中、后序遍历（递归实现）

二叉树是一个非线性的数据结构，对它进行遍历的方式其实有多种，因此如果我们都以自己的方式去遍历二叉树，那么这个代码的易懂性就大大降低，显得很混乱。

为此对于二叉树，根据遍历根节点的先后次序，我们有以下三种遍历方式（N：代表根节点；L：代表根节点的左子树；R：代表根节点的右子树）

  • 前序遍历（NLR）： 先访问根节点➡根的左子树➡根的右子树
  • 中序遍历（LNR）： 先访问根的左子树➡根节点➡根的右子树
  • 后序遍历（LRN）： 先访问根的左子树➡根的右子树➡根节点

练习题：

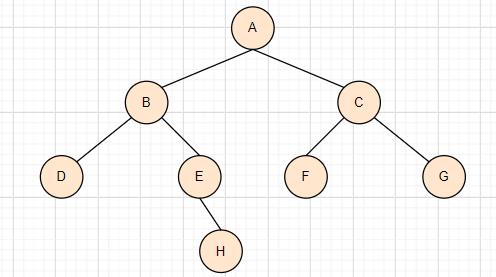
请写出下面这棵二叉树的四种遍历方式

答案：

  • 前序遍历：ABDEHCFG
  • 中序遍历：DBEHAFCG
  • 后序遍历：DHEBFGCA

注意：

不管是前序、中序还是后序遍历，遍历的路径是一样的，但访问的方式是不一样的

2.6.2 二叉树的层序遍历

除了前中后序遍历外，二叉树还有一种很直观的遍历方式：层序遍历。层序遍历就是从二叉树的根节点出发，首先访问该树的第一层的根节点，然后从左到右访问第二层的节点，接着是第三层的节点，以此类推。

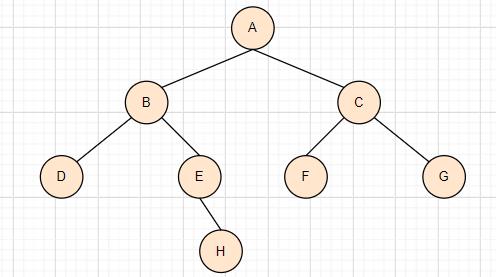
对于上图的树，使用层序遍历，节点被访问的顺序为：ABCDEFGH

层序遍历一般使用非递归的方式，具体的实现方法可以使用队列。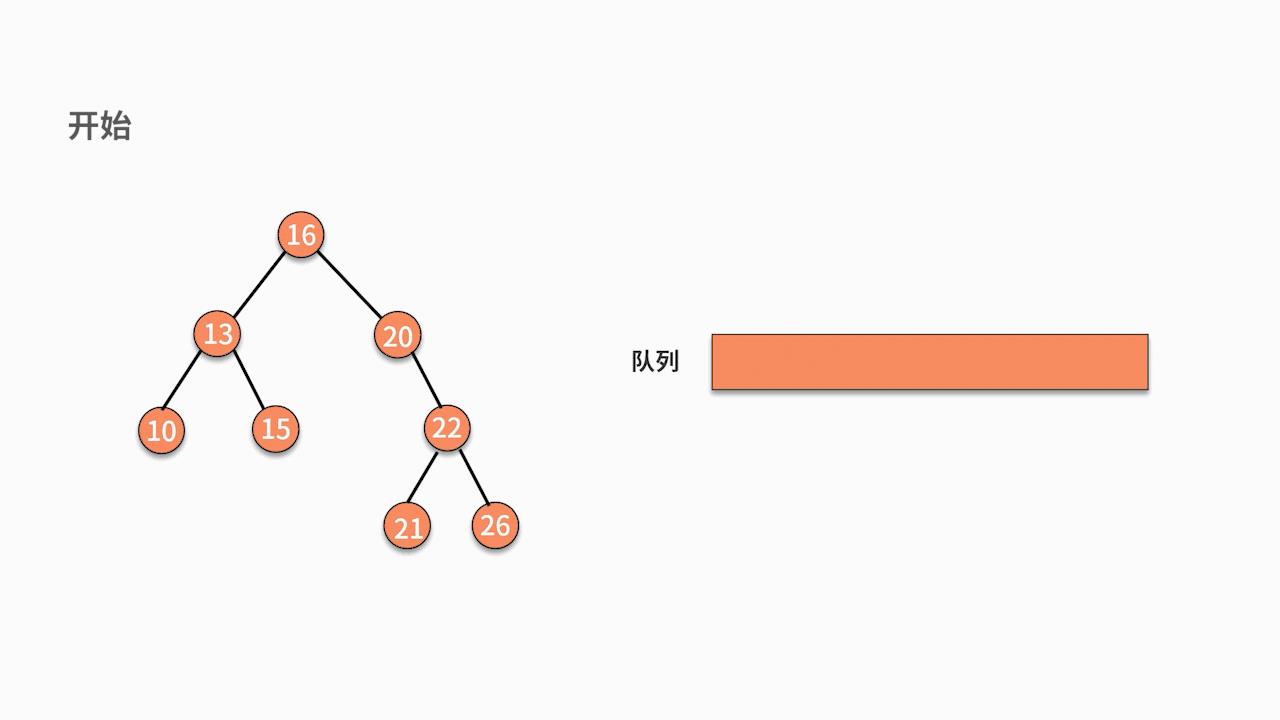

代码： 实现层序遍历

public void levelOrderTraversal(Node root){
    if(root==null){
        return;
    }
    Queue<Node> queue=new LinkedList<>();
    queue.offer(root);
    while(!queue.isEmpty()){
        Node node=queue.poll();
        System.out.print(node.val+" ");
        if(node.left!=null) {
            queue.offer(node.left);
        }
        if(node.right!=null) {
            queue.offer(node.right);
        }
    }
}

相关习题：

  • 习题一： 求一棵树的左视图

    代码：

    public List<Character> leftMap(Node root) {
    List<Character> ret=new ArrayList<>();
    if(root==null){
        return ret;
    }
    Queue<Node> queue =new LinkedList<>();
    queue.offer(root);
    while(!queue.isEmpty()){
        int size=queue.size();
        int count=size;
        while(size>0){
            Node top=queue.poll();
            if(count==size){
                ret.add(top.val);
            }
            if(top.left!=null){
                queue.offer(top.left);
            }
            if(top.right!=null){
                queue.offer(top.right);
            }
            size--;
        }
    }
    return ret;
}

  • 习题二： 求二叉树的最大宽度

    代码：

    public int maxWidth(Node root) {
    if(root==null){
        return 0;
    }
    Queue<Node> queue =new LinkedList<>();
    queue.offer(root);
    int max=0;
    while(!queue.isEmpty()){
        int size=queue.size();
        max=Math.max(max,size);
        while(size>0){
            Node top=queue.poll();
            if(top.left!=null){
                queue.offer(top.left);
            }
            if(top.right!=null){
                queue.offer(top.right);
            }
            size--;
        }
    }
    return max;
}

  • 习题三： 判断一棵树是不是完全二叉树

    代码：

    public boolean isCompleteTree(Node root){
    if(root==null){
        return true;
    }
    Queue<Node> queue=new LinkedList<>();
    queue.offer(root);
    while(!queue.isEmpty()){
        Node top=queue.poll();
        if(top==null){
            break;
        }
        queue.offer(top.left);
        queue.offer(top.right);
    }
    while(!queue.isEmpty()){
        Node top=queue.peek();
        if(top!=null){
            return false;
        }
        queue.poll();
    }
    return true;
}

2.6.2 二叉树的实现

由于二叉树的创建一般使用递归，而递归创建二叉树将在后面重点介绍。故这里使用穷举法来创建下面这棵二叉树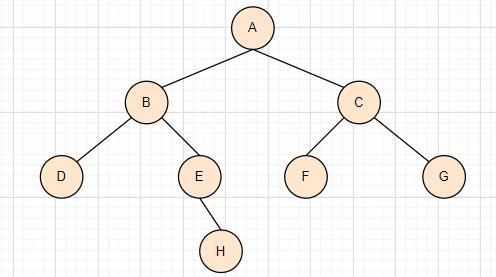

实现代码：

class Node{
    public char val;
    public Node left;
    public Node right;
    public Node(char val){
        this.val=val;
    }
}
public class TestBinaryTree {

    // 使用穷举的方式创建一棵二叉树
    public Node createTree(){
        Node A=new Node('A');
        Node B=new Node('B');
        Node C=new Node('C');
        Node D=new Node('D');
        Node E=new Node('E');
        Node F=new Node('F');
        Node G=new Node('G');
        Node H=new Node('H');
        A.left=B;
        A.right=C;
        B.left=D;
        B.right=E;
        E.right=H;
        C.left=F;
        C.right=G;
        return A;
    }

    // 前序遍历
    public void preOrderTraversal(Node root){
        if(root==null) {
            return;
        }
        System.out.print(root.val+" ");
        preOrderTraversal(root.left);
        preOrderTraversal(root.right);

    }

    // 中序遍历
    public void inOrderTraversal(Node root) {
        if (root == null) {
            return;
        }
        inOrderTraversal(root.left);
        System.out.print(root.val+" ");
        inOrderTraversal(root.right);
    }

    // 后序遍历
    public void posOrderTraversal(Node root){
        if(root==null){
            return;
        }
        posOrderTraversal(root.left);
        posOrderTraversal(root.right);
        System.out.print(root.val+" ");
    }

    // 遍历思路-求节点个数
    public static int size=0;
    public void getSize1(Node root){
        if(root==null){
            return;
        }
        size++;
        getSize1(root.left);
        getSize1(root.right);
    }

    // 子问题思路-求节点个数
    public int getSize2(Node root){
        if(root==null){
            return size;
        }
        int val=1+getSize2(root.left)+getSize2(root.right);
        return val;
    }

    // 遍历思路-求叶子节点个数
    public static int leafSize;
    public void getLeafSize1(Node root){
        if(root==null){
            return;
        }
        if(root.left==null&&root.right==null){
            leafSize++;
            return;
        }
        getLeafSize1(root.left);
        getLeafSize1(root.right);
    }

    // 子问题思路-求叶子节点个数
    public int getLeafSize2(Node root){
        if(root==null){
            return 0;
        }
        if(root.left==null&&root.right==null) {
            return 1;
        }
        int val=getLeafSize2(root.left)+getLeafSize2(root.right);
        return val;
    }

    // 第 k 层的节点个数
    public int getKLeafSize(Node root,int k){
        if(root==null){
            return 0;
        }
        if(k==1){
            return 1;
        }
        int val=getKLeafSize(root.left,k-1)+getKLeafSize(root.right, k-1);
        return val;
    }

    // 获取当前二叉树的高度
    public int getHeight(Node root){
        if(root==null){
            return 0;
        }
        return 1+Math.max(getHeight(root.left),getHeight(root.right));
    }

    // 查找二叉树的某个节点
    public Node find(Node root,char val){
        if(root==null){
            return null以上是关于数据结构 Java 版二叉树的实现（超多图超详解）的主要内容，如果未能解决你的问题，请参考以下文章
 

 数据结构C语言版二叉树的结构和遍历的实现


 [数据结构] 树与二叉树的超详细解析 建议收藏 看它就够了


 平衡树初阶——AVL平衡二叉查找树+三大平衡树（Treap + Splay + SBT）模板超详解


 数据结构 Java 版堆和优先级队列（超详解）


 数据结构 Java 版堆和优先级队列（超详解）


 数据结构中二叉树的顺序存储结构代码怎么编写？