[计算机数值分析]开方公式-牛顿法

Posted 2022-01-10 Spring-_-Bear

问题描述

对于给定的正整数 c，应用牛顿法解二次方程 x² - c = 0，可导出开方值根号 c 的计算公式 x₁ = x₀ - （x₀ - c²) / 2x₀，也即 x₁ = 1 / 2 *(x₀ + c / x₀), 设 x₁ 是根号 c 的某个近似值，则 c / x₀ 自然也是一个近似值，从以上的分析中不难看出，它们两者的算术平均值将是更好的近似值。

例：应用牛顿法求根号 115 的值。取迭代初值 x₀ = 10，精度要求 0.000001.

运行示例

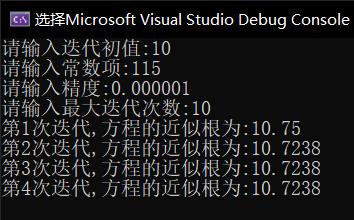
源码

//牛顿法-开方公式
#include<iostream>
#include<cmath>
using namespace std;

double f(double x, int c);   //f(x)为x的平方减去常数C
double f1(double x);   //f1(x)为f(x)的一阶导数即2x

int main(void)

	double accuracy, N;  //accuracy为精度；N为最大迭代次数;
	double x0, x1;    //x0为运用牛顿法时选取的初值;x1为迭代初值的下一次迭代值
	int C, count;   //C为给定的常数;count为当前迭代次数

	cout << "请输入迭代初值:";
	cin >> x0;
	cout << "请输入常数项:";
	cin >> C;
	C = abs(C);   //保证常数项为正值
	cout << "请输入精度:";
	cin >> accuracy;
	cout << "请输入最大迭代次数:";
	cin >> N;

	count = 0;

	do
	
		count++;   //迭代次数自增1

		if (count > N)   //迭代次数达到限制
		
			cout << "达到允许的最大迭代次数！迭代结束！" << endl;
			break;
		

		if (f1(x0) == 0)   //一阶导数值为0，无法进行牛顿迭代
		
			cout << "在x0附近f(x)的一阶导数值为0，不适用牛顿法求方程的根!" << endl;;
			break;
		
		else
		
			x1 = x0 - f(x0, C) / f1(x0);

			cout << "第" << count << "次迭代,方程的近似根为:" << x1 << endl;

			//交换x0与1的值，便于进行下一次迭代
			double temp;
			temp = x1;
			x1 = x0;
			x0 = temp;
		
	 while (abs(x1 - x0) > accuracy);

	return 0;


double f(double x, int c)   //原函数

	double result = pow(x, 2) - c;
	return result;


double f1(double x)    //导函数

	double result = 2 * x;
	return result;