高等数学伽马函数与斯特林公式
Posted 九死九歌
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了高等数学伽马函数与斯特林公式相关的知识,希望对你有一定的参考价值。
伽马函数的背景
1728年,哥德巴赫在考虑数列插值的问题,通俗的说就是把数列的通项公式定义从整数集合延拓到实数集合,例如数列1,4,9,16…可以用通项公式n²自然的表达,即便 n 为实数的时候,这个通项公式也是良好定义的。直观的说也就是可以找到一条平滑的曲线y=x²通过所有的整数点(n,n²),从而可以把定义在整数集上的公式延拓到实数集合。一天哥德巴赫开始处理阶乘序列1,2,6,24,120,720,…,我们可以计算2!,3!,是否可以计算2.5!呢?我们把最初的一些(n,n!)的点画在坐标轴上,确实可以看到,容易画出一条通过这些点的平滑曲线。

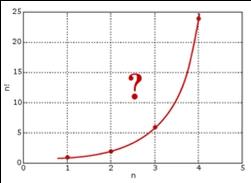
但是哥德巴赫无法解决阶乘往实数集上延拓的这个问题,于是写信请教尼古拉斯·伯努利和他的弟弟丹尼尔·伯努利,由于欧拉当时和丹尼尔·伯努利在一块,他也因此得知了这个问题。欧拉于1729 年解决了这个问题,由此导致了伽玛函数的诞生,当时欧拉只有22岁。
伽马函数的推导过程
对
1
1
−
x
进
行
离
散
展
开
:
对\\frac11-x进行离散展开:
对1−x1进行离散展开:
1
1
−
x
=
Σ
k
=
0
∞
x
k
\\frac11-x=\\Sigma^\\infty_k=0x^k
1−x1=Σk=0∞xk
再
对
他
进
行
连
续
展
开
:
再对他进行连续展开:
再对他进行连续展开:
1
1
−
x
=
∫
0
+
∞
e
−
(
1
−
x
)
t
d
t
=
∫
0
+
∞
e
−
t
⋅
e
x
t
d
t
=
∫
0
+
∞
e
−
t
⋅
Σ
k
=
0
∞
(
x
t
)
k
k
!
d
t
=
Σ
k
=
0
∞
∫
0
+
∞
e
−
t
t
k
d
t
k
!
x
k
\\frac11-x=\\int^+\\infty_0e^-(1-x)tdt\\\\=\\int^+\\infty_0e^-t\\cdot e^xtdt\\\\=\\int^+\\infty_0e^-t\\cdot \\Sigma^\\infty_k=0\\frac(xt)^kk!dt =\\Sigma^\\infty_k=0\\frac\\int^+\\infty_0e^-tt^kdtk!x^k
1−x1=∫0+∞e−(1−x)tdt=∫0+∞e−t⋅extdt=∫0+∞e−t⋅Σk=0∞k!(xt)kdt=Σk=0∞k!∫0+∞e−ttkdtxk
由 此 可 知 : Σ k = 0 ∞ x k = Σ k = 0 ∞ ∫ 0 + ∞ e − t t k d t k ! x k 即 k ! = ∫ 0 + ∞ e − t t k d t 由此可知:\\Sigma^\\infty_k=0x^k=\\Sigma^\\infty_k=0\\frac\\int^+\\infty_0e^-tt^kdtk!x^k\\\\ 即k!=\\int^+\\infty_0e^-tt^kdt 由此可知:Σk=0∞xk=Σk=0∞k!∫0+∞e−ttkdtxk即k!=∫0+∞e−ttkdt
我
们
设
伽
马
函
数
Γ
(
x
+
1
)
=
x
!
=
∫
0
+
∞
e
−
t
t
x
d
t
我们设伽马函数\\Gamma(x+1)=x!=\\int^+\\infty_0e^-tt^xdt
我们设伽马函数Γ(x+1)=x!=∫0+∞e−ttxdt
Γ
(
x
)
=
∫
0
+
∞
e
−
t
t
x
−
1
d
t
\\Gamma(x)=\\int^+\\infty_0e^-tt^x-1dt
Γ(x)=∫0+∞e−ttx−1dt
伽马函数与斯特林公式
lim
x
→
∞
Γ
(
x
)
=
2
π
e
−
x
x
x
−
1
2
\\lim_x\\rightarrow\\infty \\Gamma(x)=\\sqrt2\\pie^-xx^x-\\frac12
x→∞limΓ(x)=2πe−xxx−21
lim
x
→
∞
x
!
=
2
π
x
(
x
e
)
x
\\lim_x\\rightarrow\\inftyx!=\\sqrt2\\pi x(\\fracxe)^x
x→∞limx!=2πx(ex)x
以上是关于高等数学伽马函数与斯特林公式的主要内容,如果未能解决你的问题,请参考以下文章