极大极小搜索(α-β剪枝)_C++简单模拟

Posted 2021-12-20 一只特立独行的猫

文章目录

• • 与/或树
  • 博弈树
  • α-β剪枝
  • 完整模拟代码

网上大多数讲α-β剪枝算法的都是从博弈树开始讲起，但是我学过以后发现这样讲不太好理解， 所以打算从与/或树开始讲起，然后再引入博弈树，最后讲α-β剪枝。

与/或树

在解一个问题时，如果构造了一个解空间树求问题的最优解，那么必然是类似的这样一种情况。其中，红色结点为可解结点，有自己的解代价，而黑色结点为不可解结点，解的代价为$+\infty$

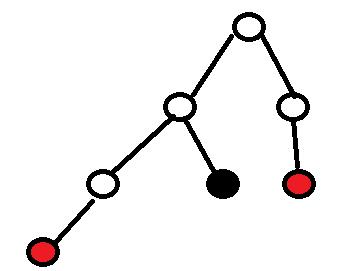
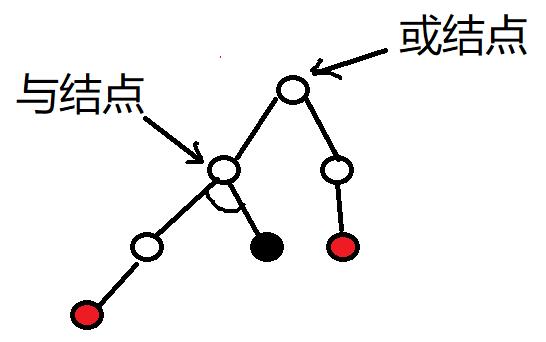
但是这样一棵树可以的解代价还无法计算，所以要引入一种解规则。就是与/或规则。一个非叶结点，可以由子节点的与操作（所有情况全部满足）或者或操作（满足一个情况即可）组成。
与操作=max子节点，或操作=min子节点

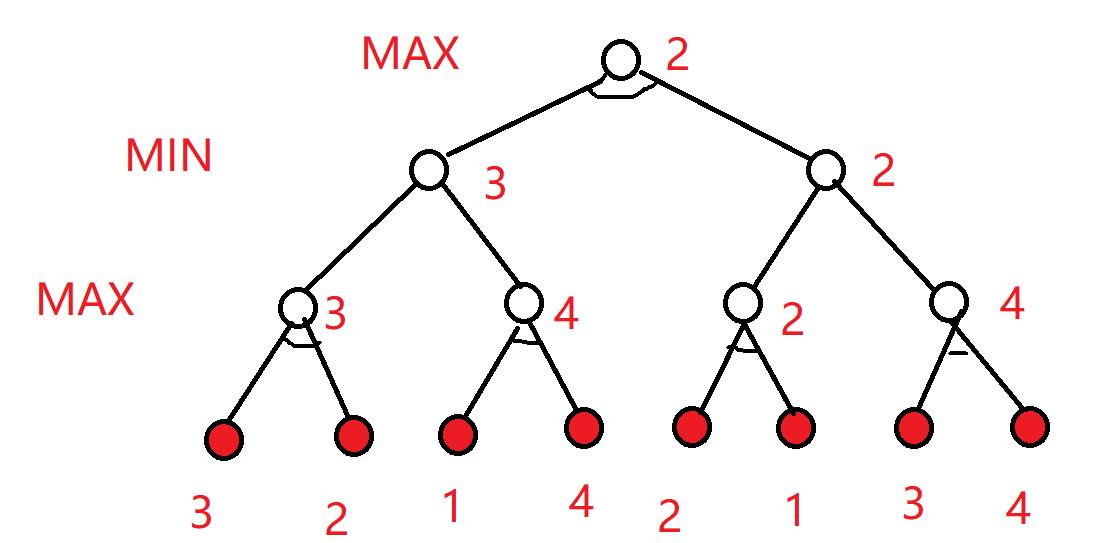
博弈树

博弈树就是一种特殊的与/或树。假设有两个绝对理性的人进行棋盘博弈，那么在其中一个人落子时，必然要考虑当前局面的最优解。假设当前棋局对他有一个分值，那么他落子时，需要考虑对他自己最优，对对方最劣的情况。那么博弈树就成了这样一棵与/或树。
博弈树一般是偶数层，因为考虑到最后肯定是对自己的落子，如果是奇数层，就是最后一步考虑了地方落子，变数更大。实际操作中偶数层博弈树的效果也比奇数层要好。

α-β剪枝

就是对博弈树进行了优化，减少解空间的计算。
对每一个非叶结点，设置一个α和β值，α表示子节点的最大值，β表示子节点的最小值。实际上，一个节点会用到一个值。MAX层的结点用到α，MIN层的结点用到β。
剪枝的思想就是这样：

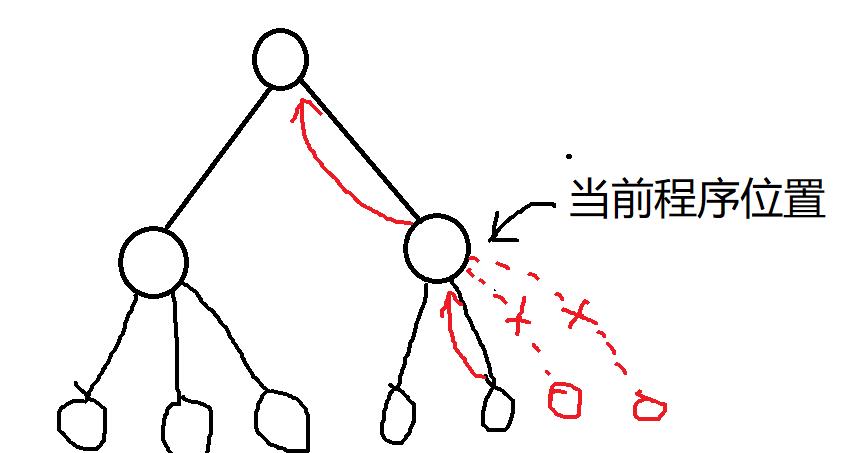
前提：任何结点只会对他的父节点产生影响。
满足如下规则的剪枝算法：
1.如果MAX层的α值大于父节点的β值，对当前结点进行剪枝。
2.如果MIN层的β值小于父节点的β值，对当前结点进行剪枝。
至于为什么这么做，可以参考一下α（子节点的最大值）和β（子节点的最小值）的意义，然后想一想就可以想通。
提示一下：

1.如果当前节点在MAX层，那么如果更新α，α只会更大，而当前节点要对父节点（MIN层）产生影响，则α必须比父节点的β更小，如果当前节点的α以及比父节点的β大了，则没有必要继续往下执行，因为当前节点一定不会对父节点产生影响了。

2.如果当前节点在MIN层，那么如果更新β，β只会更小，而当前节点要对父节点（MAX层）产生影响，则β必须比父节点的α更大，如果当前节点的β已经比父节点的α小了，则没有必要往下执行，因为当前节点一定不会对父节点产生影响了。

完整模拟代码

#include<iostream>

using namespace std;

const int MAX = 0x32769;
const int MIN = -1;

int dis;//每个节点的分叉数量
int high;//树的高度，根节点为1

void get(int leave,int &prealpha,int &prebeta) 
	//leave标识当前层数，prealpha标识父节点的alpha，prebeta标识父节点的beta
	int alpha = MIN, beta = MAX;
	if (leave == high) 
		//进入叶子节点,返回一个0~32768的随机数
		int k = rand();//给这个叶子节点一个权值
		if (leave%2 == 0) 
			//上一层是MAX层，可以更新alpha
			if (k > prealpha) 
				prealpha = k;
			
		
		else 
			//上一层是MIN层
			if (k < prebeta) 
				prebeta = k;
			
		
		cout <<"叶子节点："<<k <<endl;
		return ;
	
	if (leave%2 == 0) 
		//当前在MIN层
		for (int i = 0; i < dis; i++) 
			get(leave + 1, alpha, beta);
			if (beta <= prealpha) 
				//剪枝
				break;
			
		
		if (beta > prealpha) 
			prealpha = beta;
		
	
	else 
		//当前在MAX层
		for (int i = 0; i < dis; i++) 
			get(leave + 1, alpha, beta);
			if (alpha >= prebeta) 
				//剪枝
				break;
			
		
		if (alpha < prebeta) 
			prebeta = alpha;
		
	
	cout << leave << "层：alpha " << alpha << "  beta " << beta << endl;


int main() 
	//alpha-beta剪枝算法，alpha存放最大值，beta存放最小值
	//评估函数用rand函数代替
	cout << "请输入博弈树的高度（根节点为第一层，high<=5）" << endl;
	cin >> high;					//读入叶子节点的数量
	cout << "请输入每个节点的分叉数" << endl;
	cin >> dis;
	int alpha = MIN, beta = MAX;
	for (int i = 0; i < dis; i++) 
		get(2, alpha, beta);//根节点不需要剪枝      
	
	cout << endl;
	cout << alpha << endl;
	return 0;

结果如下：