基于FPGA的一维卷积神经网络CNN的实现

Posted 2021-12-19 Crazzy_M

理论建立与效果展示

环境：Vivado2019.2。
Part：xcku040-ffva1156-2-i，内嵌DSP个数 1920个，BRAM 600个也就是21.1Mb。

说明：通过识别加高斯白噪声的正弦波、余弦波、三角波较简单的实例来利用FPGA实现一维CNN网络，主要是实现CNN网络的搭建。
也就是将下列数据传输至FPGA，识别出下面哪些是正弦波、余弦波、三角波，通过简单实例实践，在融会贯通，最终实现雷达辐射源调制方式识别。

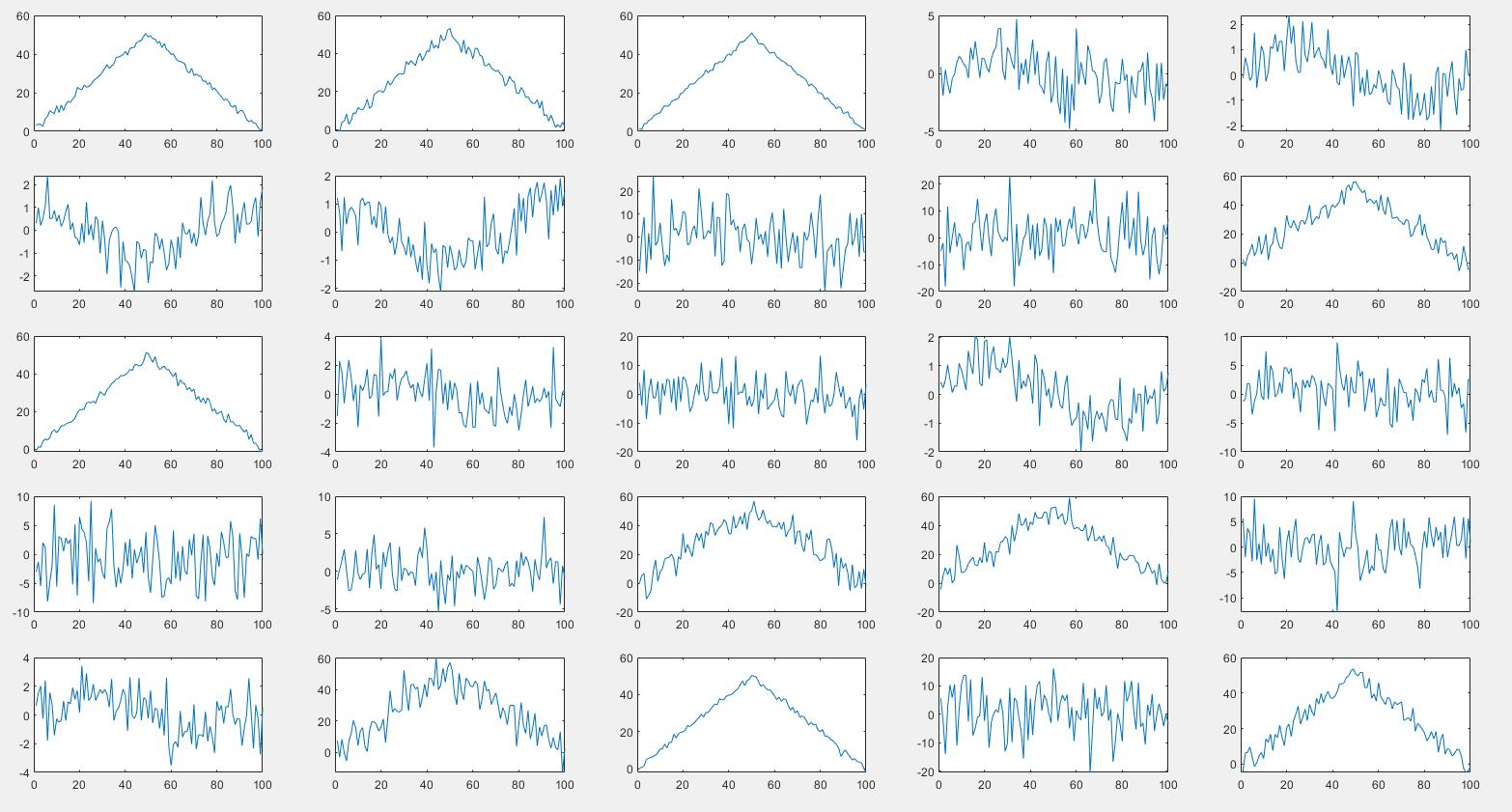
实现流程：
训练参数：通过pytorch对10000个训练集进行训练获得训练参数，反向计算不在FPGA中实现。
数据产生：Matlab产生1000个测试集。
数据传输：通过Pcie高速总线将数据传输到FPGA中进行识别。
实践效果：信噪比在 -20~5dB之间识别率100%。
数据长度：100。
CNN网络：第一层卷积：1个通道，6个卷积核，卷积核元素为5。
CNN网络：池化。
CNN网络：第二层卷积：6个通道，16个卷积核，卷积核元素为5。
CNN网络：池化。
CNN网络：第三层卷积：16个通道，16个卷积核，卷积核元素为5。
CNN网络：全连接。
CNN时效：100M时钟下，一条长度为100的数据识别耗时239个时钟周期，也就是2390ns=2.39us（因为综合实践太长了，还没实现最优，网络中有可以优化的地方，可以控制在200个时钟周期，也就是2us左右，也就是长度为100的数据的第一个数据到达FPGA到波形识别完成耗时为2us）。

文章目录

• • 一、卷积层
  • • 1.二维卷积
    • 2.一维卷积
  • 二、池化层
  • 三、全连接层
  • 四、网络搭建与演示
  • 五、温故知新
  • 六、结果展示
  • • 1.正弦波识别
    • 2.余弦波识别
    • 3.三角波识别
  • 七、资源占用情况

---

对CNN网络先进行简单介绍，详细了解请移至互联网。

一、卷积层

数学表达式

连续形式：
$$\mathrm{f}\ast \mathrm{g}={\int }_{-\infty }^{\infty }f(\tau )g(t-\tau )d\tau$$
离散形势：
$$\mathrm{f}\ast \mathrm{g}=\sum _{\tau =-\infty }^{\infty }f(\tau )g(n-\tau )$$

先对g函数进行向左翻转，然后再把g函数平移到n，在这个位置两个函数对应点相乘，再把所有位置相乘的结果相加。

1.二维卷积

二维卷积matlab演示：

5×5的矩阵a与3×3的矩阵b相卷积：

二维卷积图示（图中卷积核翻转还是和原来一样）：

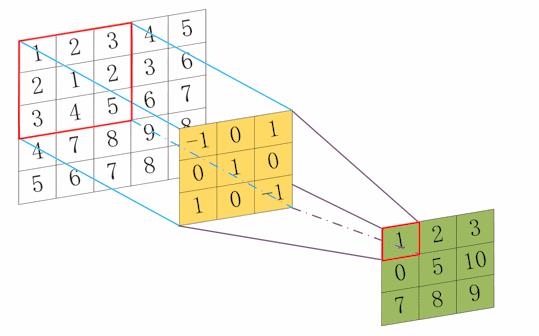
所谓两个函数的卷积，本质上就是先将一个函数翻转，然后进行滑动相应位置相乘然后再叠加。

2.一维卷积

一维卷积matlab演示：

一维卷积图示（注意卷积核是翻转后的）：

卷积结果的长度=数据长度+卷积核长度-1。

总而言之卷积的本质就是 翻转→滑动（对应相乘）→叠加的结果。

二、池化层

池化即降采样，即降低数据的大小，池化方法主要有最大池化、平均池化，其中最常用的就是最大池化。

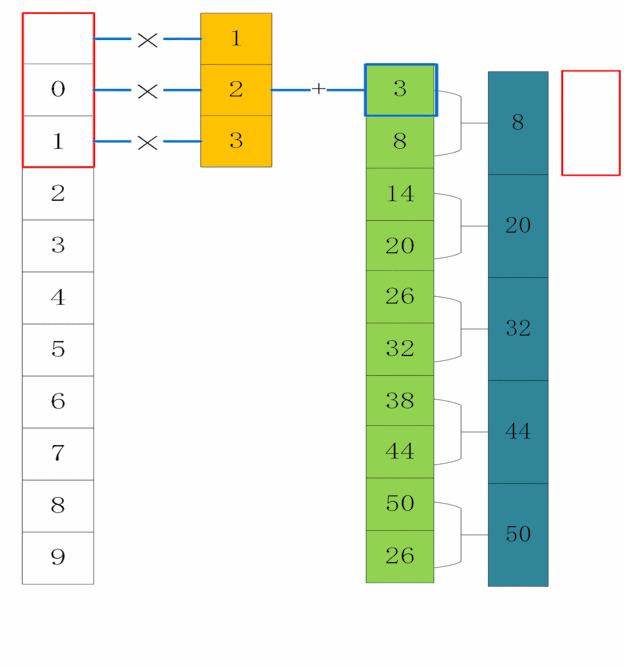
一维最大池化过程：
简而言之就是在卷积结果中以步长为2提取相邻结果的最大值。减少了特征，导致参数减少，进而简化卷积网络计算时的复杂度。

数据长度为10，卷积的结果我们取和数据长度一样的长度，池化结果的长度为5。

三、全连接层

这里只说怎么做，原理自行了解，简而言之就是将最终多个通道的卷积结果拼接成一条数据。

四、网络搭建与演示

波形识别网络如下：

网络层	输入	详细	输出
第一层卷积	1通道 100点数据	6个卷积核，卷积核元素为5	6通道 每通道100点数据
第一层池化	6通道 每通道100点数据	最大池化	6通道 每通道50点数据
第二层卷积	6通道 每通道50点数据	16个卷积核，卷积核元素为5	16通道 每通道50点数据
第二层池化	16通道 每通道50点数据	最大池化	16通道 每通道25点数据
第三层卷积	16通道 每通道25点数据	16个卷积核，卷积核元素为5	16通道 每通道25点数据
全连接	16通道 每通道25点数据	数据拼接	1通道 400点数据

网络层参数分析：
训练、训练、训练，训练的结果是什么？无非就是下面的权重和偏置参数。知道这些参数导入到FPGA搭建的加速网络里面，完整的人工智障CNN就搭建出来了。

网络层	通道数	核和核内元素	权重个数	偏置个数	总
第一层卷积	1	6个核，每个核5个元素	1×6×5	6	36
第二层卷积	6	16个核，每个核5个元素	6×16×5	16	496
第三层卷积	16	16个核，每个核5个元素	16×16×5	16	1296
全连接	1	三种波形，最后一层卷积16通道每通道25点数据	3×400	3	1203

网络图形化展示：

第一层卷积+池化：
输入：输入为1通道，数据长度为100（我们要识别的波形数据）。
卷积核：卷积核个数为6（训练出来的）。
卷积输出：6通道，数据长度为100（池化要用的）。
池化输出：6通道，数据长度为50（下一层卷积滴输入）。

第二层卷积+池化
输入：输入为6通道，数据长度为50（上一层卷积的输出）。
卷积核：卷积核个数为16（训练出来的）。
卷积输出：16通道，数据长度为50（池化要用的）。
池化输出：16通道，数据长度为25（下一层的输入）。

第三层卷积+全连接
输入：输入为16通道，数据长度为25（上一层的输出）。
卷积核：卷积核个数为16（训练出来的）。
卷积输出：16通道，数据长度为25（全连接要用的）。
全连接输出：1通道，数据长度为400（网络最终输出一条数据）。

三层卷积做完了那到底是什么波？

全连接输出了1通道400点的数据。
全连接参数为3个通道400点的参数。
让这3个通道分别和1通道全连接的输出相乘相加输出三个数。
三个数分别对应正弦波、余弦波、三角波。

五、温故知新

总结一下：
输入：
CNN网络的输入就是下面数据集的中任意一个波形的100个点：

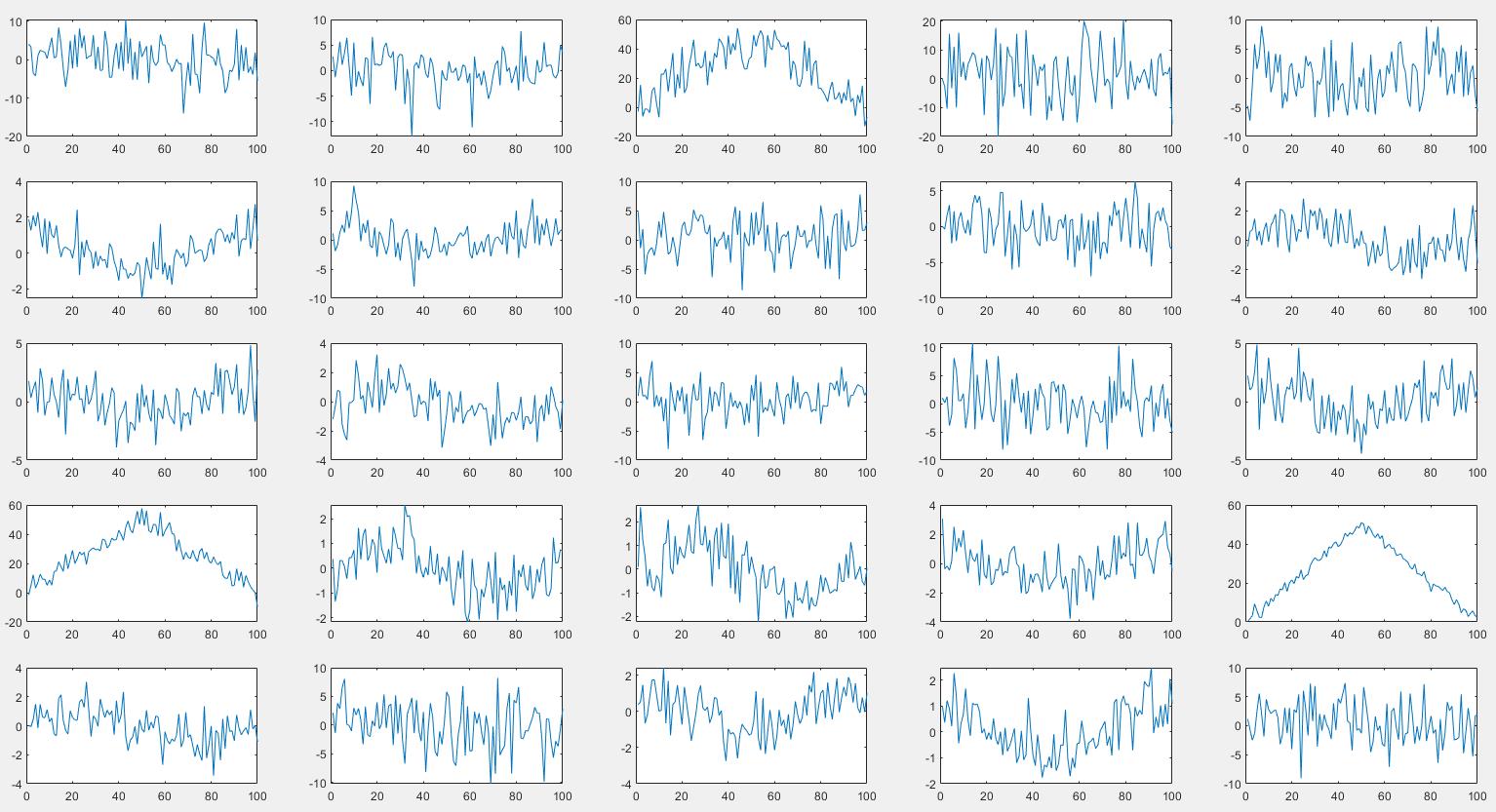
每一层的卷积核、偏置、以及全连接的权重和偏置：

每一层的卷积核、偏置是通过类似上面大量的数据集训练出来的，后面给代码，偏置其实就是卷积的结果后面加一个常量，到后面实践就知道了。

输出结果：
因为我们识别的种类为三种，我们训练的时候会给三种波形打上标签①②③，最终人工智障CNN网络就会算出三个结果，三个结果取最大的，该值对应哪个标签，就是识别结果。

六、结果展示

训练时的标签顺序为正弦波、余弦波、三角波，及最终的三个数据结果哪个大就是哪种波形。

1.正弦波识别

100点 信噪比:3.4226的正弦波导入网络

FPGA计算结果：

转换为小数：

Matlab计算结果：

2.余弦波识别

100点 信噪比:-4.8721的余弦波导入网络

FPGA计算结果：

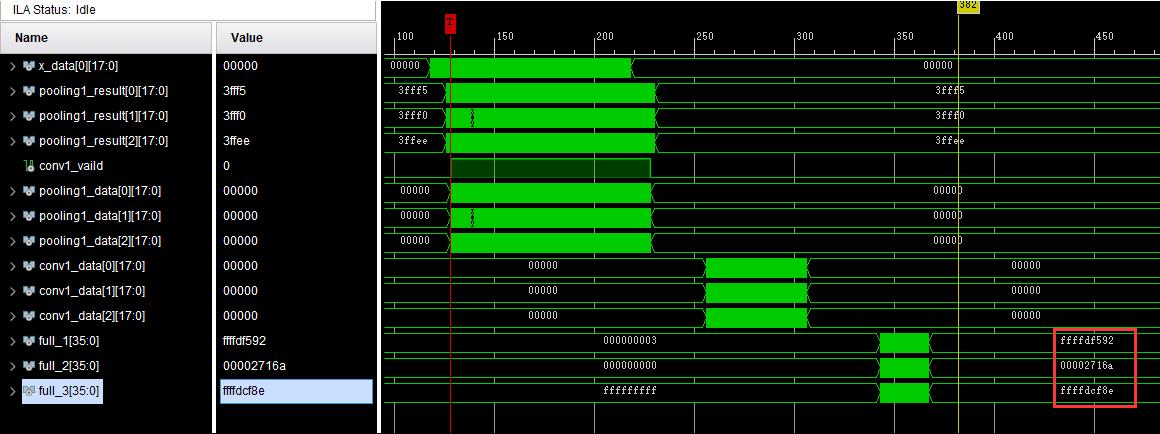
转换为小数：

Matlab计算结果：

3.三角波识别

以下100点三角波导入网络

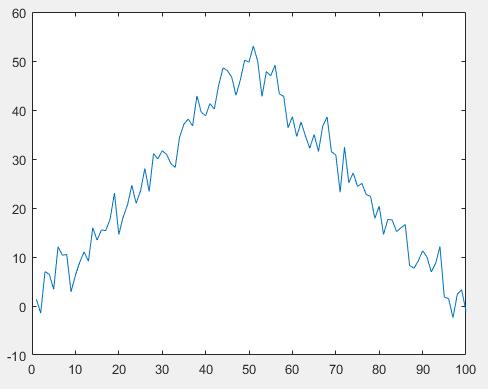
FPGA计算结果：

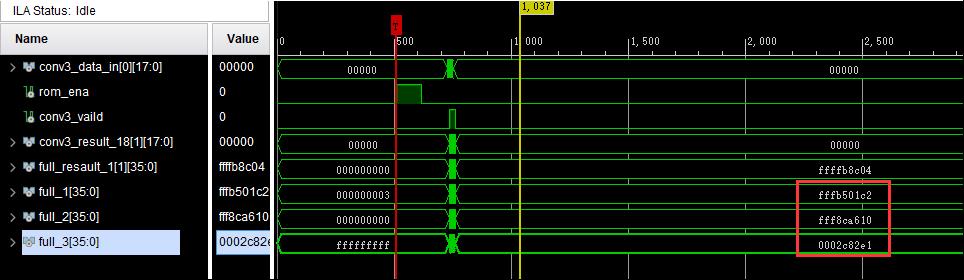
转换为小数：

Matlab计算结果：

因为涉及到数据的量化和浮点数转定点数，数据有一定的偏差，但是不会影响最终结果。

图中可以看到，当数据xdata进入FPGA开始到计算完成消耗200多个时钟周期。

七、资源占用情况

因为就想试试他最快能跑多快，所以用了大量的DSP，下一节来说这些DSP都用在了哪里。

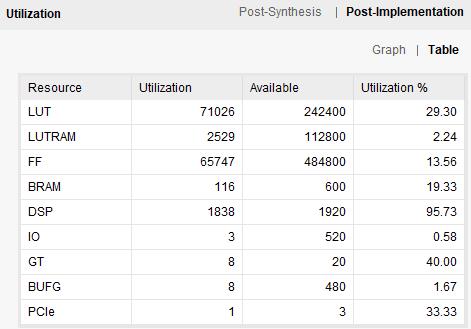
正在写。。。

★★★如有错误欢迎指导！！！