C Language 树和二叉树 - 哈夫曼树（十六）

Posted 2021-12-13 Adorable_Rocy

话不多说，直接上车~

1.初识哈夫曼树

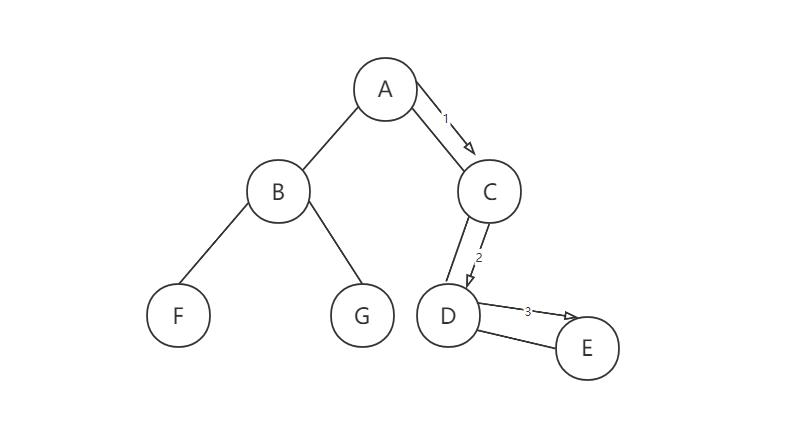
• 路径：从结点A到E之间路径为：A-C-D-E , 路径长度为3
  

• 结点带权路径长度：例如A-E之间的路径长度为3，带权路径为WPL(权重*路径长度)=3 * 8 = 24

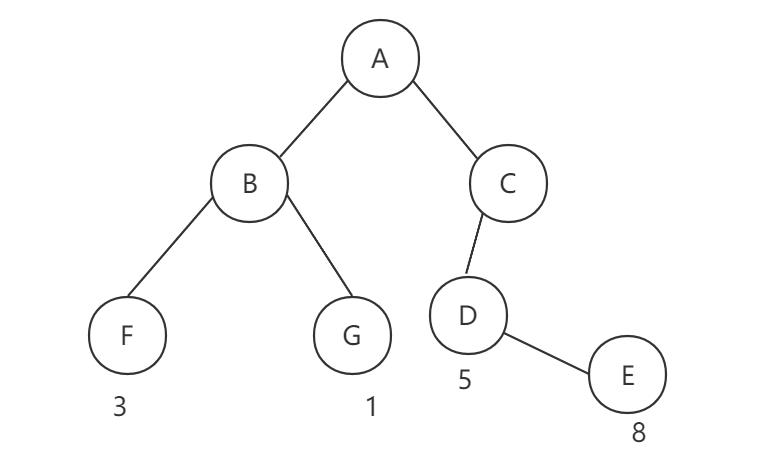
哈夫曼树的研究是什么？

在n0个带权叶子结点构成的二叉树中，带权路径长度WPL最小的二叉树成为哈夫曼树（Huffman tree）或最优二叉树。

2.创建哈夫曼树（最优二叉树构造法）

• 带权叶子结点如下：

构造方法口诀：

• 构造森林全是根

在6个根之中，1、5权重是最小的，所以单独选出来

• 选用两小造新树

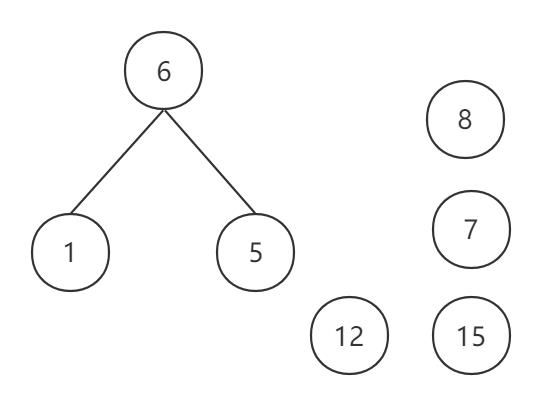
用5、6两颗小树生成新的新树

• 删除两小添新人

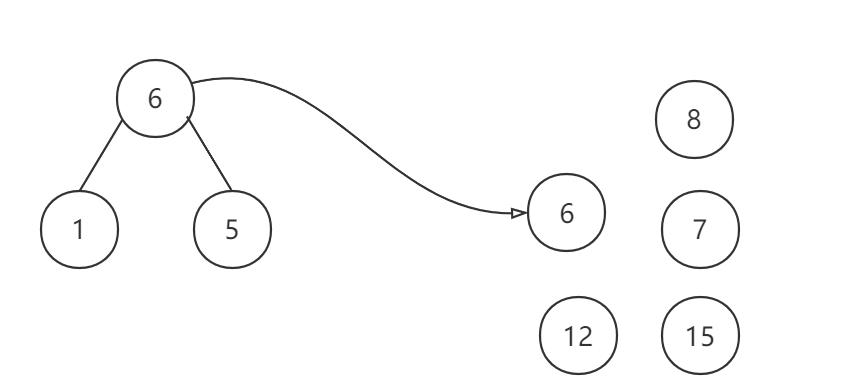
• 重复2、3剩单根

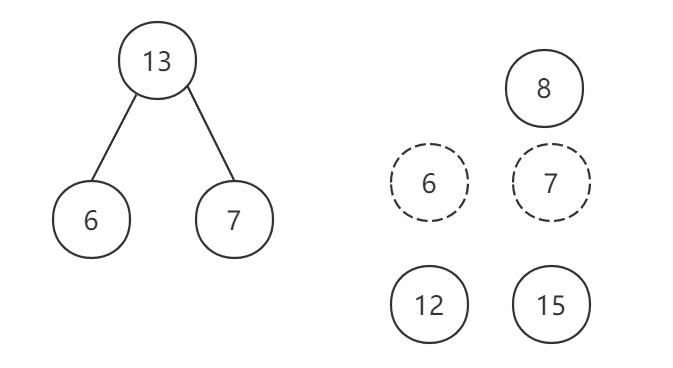
反复重复，然后完成哈夫曼树的构造

最优二叉树构成为：

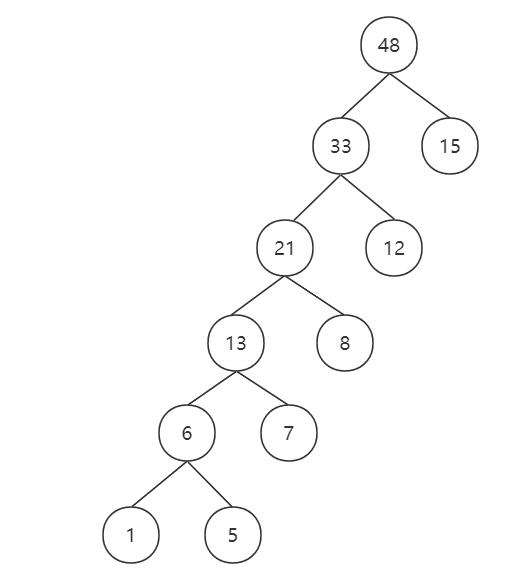
WPL=1x5+5x5+7x4+8x3+12x2+15x1 =121

一颗有n个叶子结点的哈夫曼树共有2n-1个结点

2.哈夫曼树算法：

1. 根据n0个带权值的二叉树，一共有2n-1个结点树，其带权值二叉树左右子树都为空。
2. 在森林中选取两颗权值最小的树构成新树
3. 构建2n-1个空间的数组大小用来存储所有的结点以及树
4. 用得到的新树代替之前两小树
5. 一直重复2 4 直到只含一棵树为止。

算法如下：

#include<stdio.h>
#include<malloc.h>
typedef struct HuffTree{
		int data;
		double weight;
		int parent , lchild , rchild;
}HuffTree;

void createHuffTree(HuffTree ht[] , int size , int *w){
	int index , k ,lnode , rnode;
	double min1 , min2;
	 
	for(index=0;index < size ;index++){
		ht[index].parent = ht[index].lchild = ht[index].rchild = -1; //初始化 
		ht[index].weight = w[index];
	}
	
	for(index = size ; index< 2 * size - 2; index++){
		min1 = min2 = 32767;
		lnode = rnode = -1;
		
		for(k = 0;k<=index - 1; k++){
			if(ht[k].parent == -1){
				if(ht[k].weight < min1){
					min2 = min1;rnode = lnode;
					min1 = ht[k].weight;lnode = k;
				}else if(ht[k].weight < min2){
					min2 = ht[k].weight;rnode = k;
				}
			}
			ht[index].weight=ht[lnode].weight + ht[rnode].weight;
			ht[index].lchild = lnode;ht[index].rchild = rnode;
			ht[lnode].parent=index;ht[rnode].parent = index;			 
		}
	}
}

main(){
	HuffTree *ht;
	ht = new HuffTree[MaxSize - 1];
	int w[MaxSize / 2] = {1,3,5,6,6,7,8,15};
	createHuffTree(ht,MaxSize / 2,w);
	dispTree(ht);
	return 0;
} 

3.哈夫编码：

很多时候我们也会质疑哈夫曼树到底是有什么用，为什么叫它最优二叉树？下面直接给出结论

字母	e	a	c	v	z	q
频率	0.6	0.17	0.11	0.4	0.28	0.15

根据上面给出的字母的频率（虚化），其实在应用中，早就已经有科学家统计好字母的频率，可以直接进行使用

• 构造最优表示法可以使用哈夫曼树的构造口诀进行构造

1. 构建哈夫曼树
2. 左子树通过路径记作‘0’
3. 油渍树通过路径记作‘1’
4. 所有路径都是唯一并且不重复的

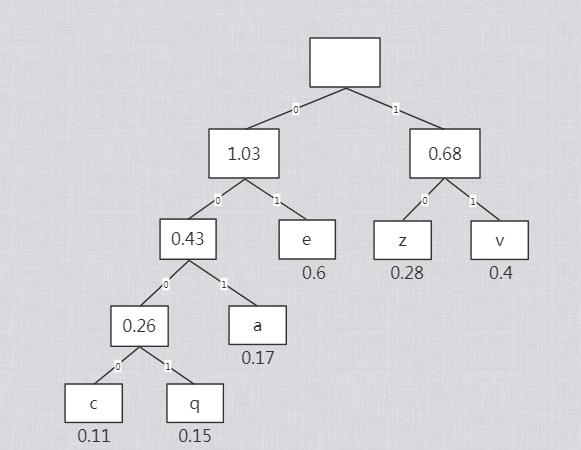
例如Q编码为：0001 A编码为：001

如何遍历呢？当遍历到的元素没有左右子树（叶子结点）时，根据编码输出字符

0110110010001101100010000…

输出结果为：ezvaqzvqc