实验3 动态规划（0/1背包）

Posted 2021-12-12 Roninaxious

1.问题给定的已知
N种物品和一个背包，物品的种类为wi，价值为vi，背包容量为C

2.所求目标
如何选择装入背包的物品，使得物品的总价值最大

3.数学模型

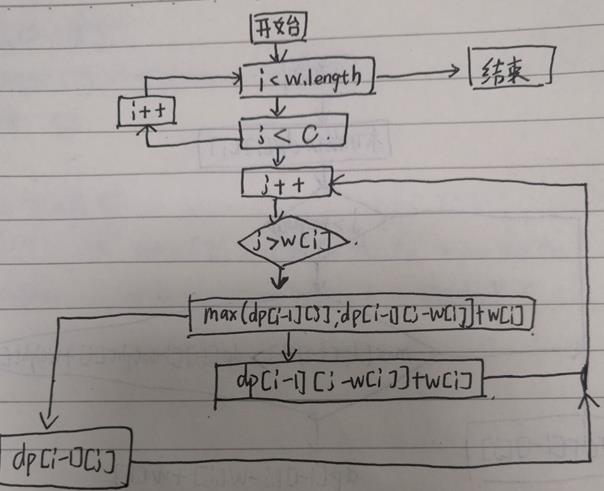
4.最优质子结构分析

现将问题分为n个子问题
（1）背包容量为c，从1号物品找出该问题的解
（2）背包容量为c，从1、2号物品找出该问题的解
（3）背包容量为c，从1、2、3号物品找出该问题的解
（4）背包容量为c，从1、2、3、4号物品找出该问题的解
……
（5）背包容量为c，从1、2、3、4、…N号物品找出该问题的解

5.建立最优值得递归关系式
递推式：M[i, j] = max{m[i+1,j]，m(i-1,j-w[i])+v[i]}
边界条件：j>=w[i]

6.程序代码

public class Package01 {

    private int[][] nums;
    private int[] weight;
    private int[] value;
    int maxWeight;
    public Package01(int[] weight, int[] value, int maxWeight) {
        this.weight = weight;
        this.value = value;
        this.maxWeight = maxWeight;
        nums = new int[weight.length + 1][maxWeight + 1];
    }

    /**
     * i代表物品
     * j代表背包容量
     */
    public void maxValue() {
        for (int i = 1; i <= weight.length; i++) {
            for (int j = 1; j <= maxWeight; j++) {
                if (j < weight[i - 1]) {
                    nums[i][j] = nums[i - 1][j];
                } else {
                    nums[i][j] = Math.max(nums[i - 1][j], nums[i - 1][j - weight[i - 1]] + value[i - 1]);
                }
            }
        }
    }
    public void print() {
        int i = nums.length;
        int j =nums[0].length;
        for (int k = 0; k < i; k++) {
            for (int s = 0; s < j; s++) {
                System.out.print(nums[k][s]+" ");
            }
            System.out.println();
        }
    }
    //测试
    public static void main(String[] args) {
        int[] weight = {1, 3, 4};
        int[] value = {1500, 2000, 3000};
        Package01 p = new Package01(weight, value, 4);
        p.maxValue();
        p.print();
    }

}

7.测试数据

第一组：

第二组:

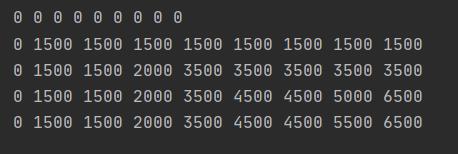
8.结果分析

测试结果正确

以上方法的时间和空间复杂度均为O(N*V）