动态规划:0-1背包问题
Posted Abro.
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了动态规划:0-1背包问题相关的知识,希望对你有一定的参考价值。
目录
前言
给定 n n n 种物品和一个背包。物品 i i i 的重量是 w i wi wi,其价值为 v i vi vi,背包的容量为 c c c。问应如何选择装入背包的物品,使得装入背包中物品的总价值最大?
一、原理
0 − 0 - 0− 1 1 1 背包问题是一个特殊的整数规划问题。
m a x max max ∑ i − 1 n v i x i {\\textstyle \\sum_{i-1}^{n}} v_{i} x_{i} ∑i−1nvixi
{ ∑ i = 1 n w i x i ≤ C x i ∈ ( 0 , 1 ) , 1 ≤ i ≤ n \\begin{cases}{\\textstyle \\sum_{i=1}^{n}} w_{i} x_{i} \\le C \\\\ x_{i} \\in (0,1),1\\le i \\le n \\end{cases} {∑i=1nwixi≤Cxi∈(0,1),1≤i≤n
1.1 最优子结构性质
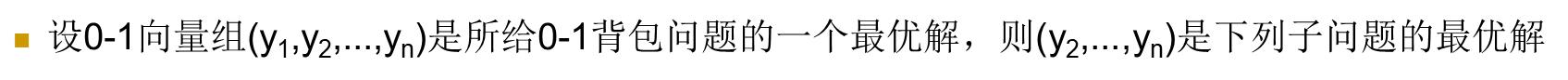
m
a
x
max
max
∑
i
=
2
n
v
i
x
i
{\\textstyle \\sum_{i=2}^{n}} v_{i} x_{i}
∑i=2nvixi
{ ∑ i = 2 n w i x i ≤ C − w 1 y 1 x i ∈ ( 0 , 1 ) , 2 ≤ i ≤ n \\begin{cases}{\\textstyle \\sum_{i=2}^{n}} w_{i} x_{i} \\le C-w_{1}y_{1} \\\\ x_{i} \\in (0,1),2\\le i \\le n \\end{cases} {∑i=2nwixi≤C−w1y1xi∈(0,1),2≤i≤n
1.2 递归关系
m a x max max ∑ k = i n v k x k {\\textstyle \\sum_{k=i}^{n}} v_{k} x_{k} ∑k=invkxk
{ ∑ k = i n w k x k ≤ j x k ∈ ( 0 , 1 ) , i ≤ k ≤ n \\begin{cases}{\\textstyle \\sum_{k=i}^{n}} w_{k} x_{k} \\le j \\\\ x_{k} \\in (0,1),i\\le k \\le n \\end{cases} {∑k=inwkxk≤jxk∈(0,1),i≤k≤n
设所给 0 − 1 0-1 0−1 背包问题的子问题的最优值为 m(i,j),即 m(i,j)是背包容量为 j,可选择物品为 i,i+1,…,n 时 0-1背包问题的最优值。由 0-1背包问题的最优子结构性质,可以建立计算 m(i,j)的递归式如下:
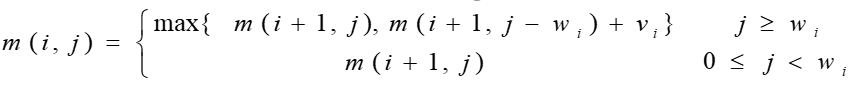
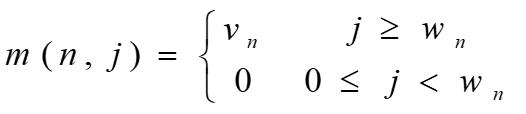
二、算法描述
2.1 算法描述
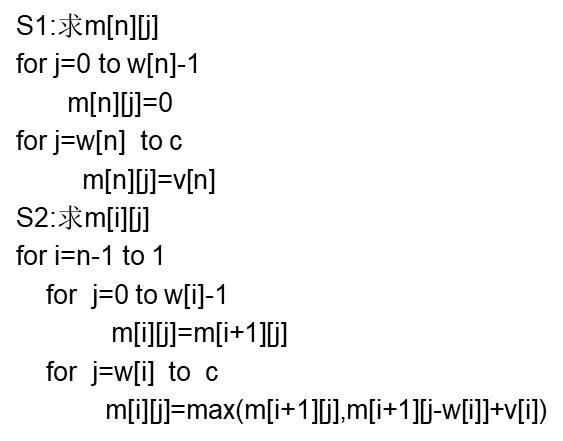
伪代码:

2.2 图解

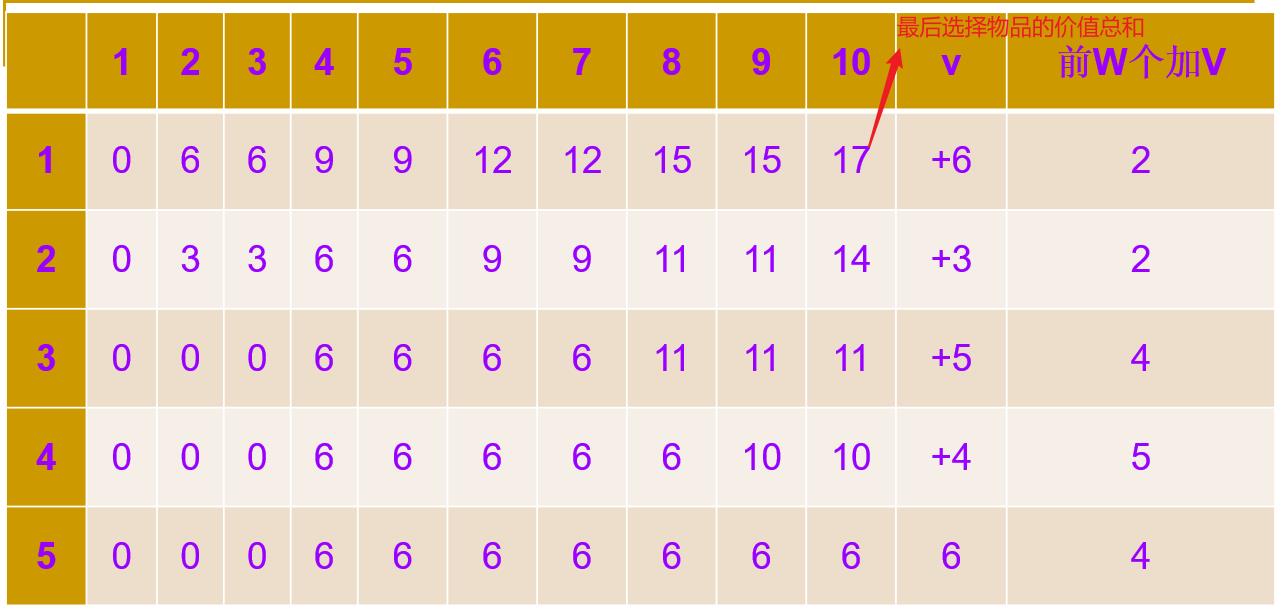
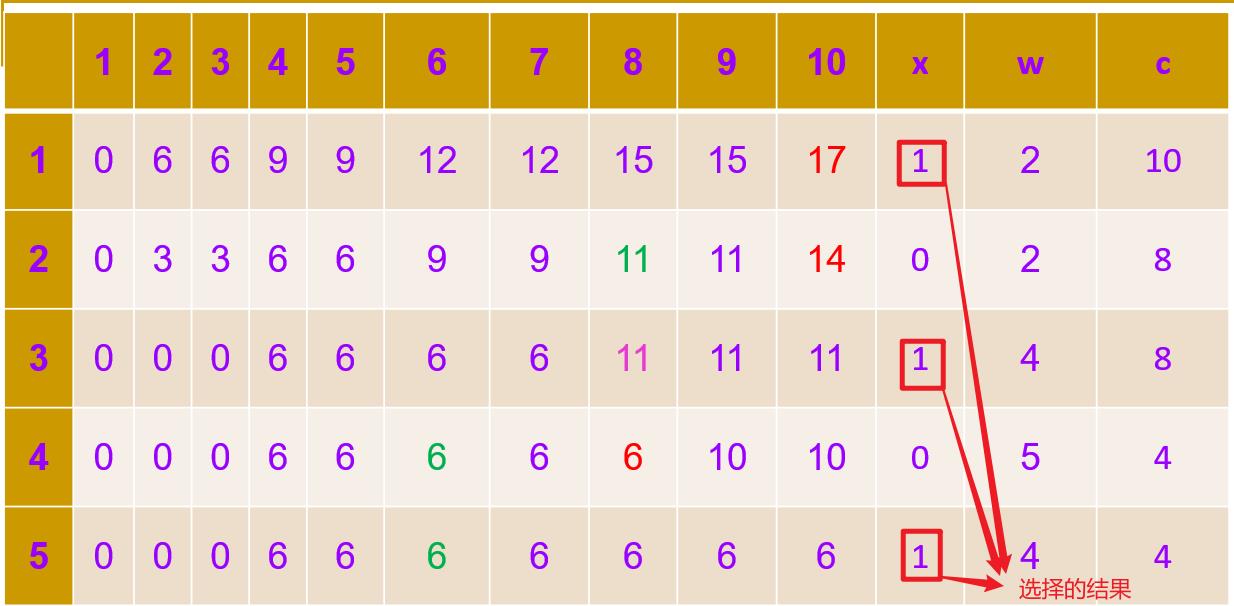
2.3 构造最优解

三、 0 − 1 0-1 0−1 背包问题相关题目
3.1 题目
已知有5个物体,它们的重量分别为:2,2,4,5,4,各物体的价值依次为6,3,5,4,6,背包大小为10,使用动态规划法求矩阵m[i][j],并给出最优解。
修改数据为:5个物体,它们的重量分别为:1,1,2,3,2,各物体的价值依次为6,3,5,4,6,背包大小为6,使用动态规划法求矩阵m[i][j],并给出最优解
3.2 源程序(Java求解 0 − 1 0-1 0−1背包问题)
/**
* 0-1背包问题(动态规划法求解)
*/
public class E3_9 {
//物品的个数+1(第一个数我写成0)
static int N = 6;
//static int C = 7;
static int C = 11;
/**
* 程序的入口
* @param args
*/
public static void main(String[] args) {
//int n = N-1;
//背包的容量
int c = C-1;
int i;
//物体的重量
//int w[] = new int[N];
int w[] = new int[]{0,2,2,4,5,4};
//int w[] = new int[]{0,1,1,2,3,2};
//物体的价值
//int v[] = new int[N];
int v[] = new int[]{0,6,3,5,4,6};
//动态规划法求解过程的矩阵
int m[][] = new int[N][C];
//选择的结果
int x[] = new int [N];
/*for (i = 1; i < N; i++) {
w[i] = 1+(int) (Math.random()*5);
v[i] = 1+(int) (Math.random()*10);
}*/
knapsack(v,w,c,m);
traceback(m,w,c,x);
System.out.printf("背包能装的最大价值为:"+"%d \\n ",m[1][c]);
for (i = 1; i <= c; i++) {
System.out.printf("%2d \\t",i);
}
System.out.printf("重量 价值\\n");
for (i = 1; i < N; i++) {
System.out.printf("%d:",i);
for (int j = 1; j <= c; j++) {
System.out.printf("%2d \\t",m[i][j]);
}
System.out.printf("%2d%4d\\n",w[i],v[i]);
}
System.out.printf("\\n\\n物品的重量");
for (i = 1; i < N; i++) {
System.out.printf("%2d \\t",w[i]);
}
System.out.printf("\\n物品的价值");
for (i = 1; i < N; i++) {
System.out.printf("%2d \\t",v[i]);
}
System.out.printf("\\n选择的结果");
for (i = 1; i < N; i++) {
System.out.printf("%2d \\t",x[i]);
}
System.out.printf("\\n");
}
/**
* 由0-1背包问题的最优子结构性质建立的递归式
* @param v 存储物品价值的数组
* @param w 存储物品重量的数组
* @param c 背包容量
* @param m 动态规划法求解过程的矩阵
*/
public static void knapsack(int []v,int []w,int c,int [][]m){
int n=v.length-1;
int jMax=Math.min(w[n]-1,c);
for(int j=0;j<=jMax;j++) m[n][j]=0;
for(int j=w[n];j<=c;j++) m[n][j]=v[n];
for(int i=n-1;i>0;i--){
jMax=Math.min(w[i]-1,c);
for(int j=0;j<=jMax;j++)
m[i][j]=m[i+1][j];
for(int j=w[i];j<=c;j++)
m[i][j]=Math.max(m[i+1][j],m[i+1]以上是关于动态规划:0-1背包问题的主要内容,如果未能解决你的问题,请参考以下文章