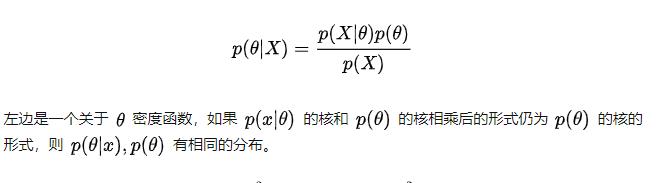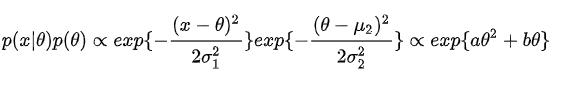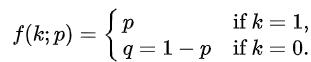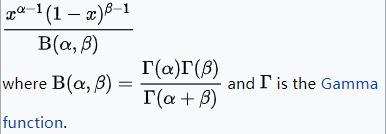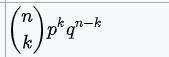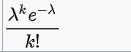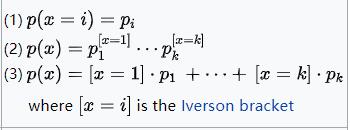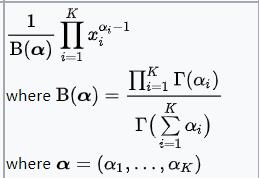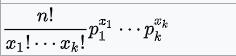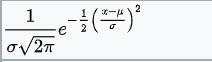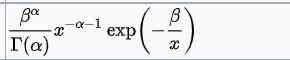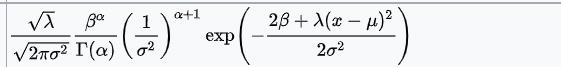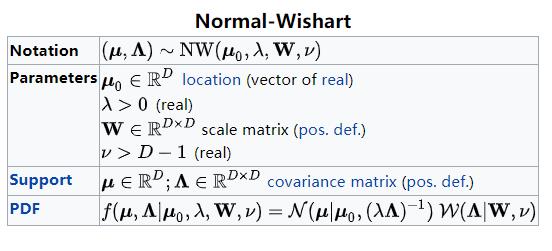概率统计笔记:共轭分布
Posted UQI-LIUWJ
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了概率统计笔记:共轭分布相关的知识,希望对你有一定的参考价值。
1 共轭的定义
在概率统计笔记:贝叶斯推断 Bayesian Inference_UQI-LIUWJ的博客-CSDN博客 中,我们有:

如果某个随机变量Θ的后验概率 p(θ|x)和先验概率p(θ)属于同一个分布簇的(有相同的形式),那么称p(θ|x)和p(θ)为共轭分布,同时,也称p(θ)为似然函数p(x|θ)的共轭先验。
换句话说:
我们以高斯分布为例,如果p(x|θ)和p(θ)都是高斯分布的话,它们的乘积也是高斯分布:
注意贝叶斯定理左边是θ的后验分布,只关心θ,所以推导时只保留θ有关的项。
此时称正态分布(贝叶斯定理中的p(x|θ),样本分布)关于均值(样本分布某参数)的共轭先验分布为正态分布(p(θ) ,参数分布)。
注意共轭先验分布是针对某一参数而言,如正态分布关于方差的共轭先验分布为倒Gamma分布。
再举一个例子,二项分布关于成功概率的共轭先验分布是贝塔分布
2 机器学习模型的角度理解共轭先验分布
我们可以将先验分布看做机器学习中的模型(比如Beta分布),那么Beta分布中的参数a,b可以作为模型状态的表示。
每次有新的训练数据(样本观测结果),我们就可以更新模型参数(根据数据将先验分布转换为后验分布),以Beta分布为例,如果数据生成过程服从二项分布,参数a,b根据数据更新后的值为a+s,b+f,其中s和f只依赖于训练数据。
那么我们可以说模型得到了“训练”,训练的结果就是模型的状态(a,b)得到了更新。
【贝塔分布是二项分布的先验分布】
2.1 共轭分布的意义
因为后验分布和先验分布形式相近,只是参数有所不同,这意味着当我们获得新的观察数据时,我们就能直接通过参数更新,获得新的后验分布,此后验分布将会在下次新数据到来的时候成为新的先验分布。
如此一来,我们更新后验分布就不需要通过大量的计算,十分方便。
3 常用共轭先验分布
来自维基百科 https://en.wikipedia.org/wiki/Conjugate_prior
3.1 离散条件概率分布
| 概率分布函数 | 关于哪个参数的共轭先验分布 | 共轭先验分布的概率分布函数 | 后验分布的参数(后验分布和先验分布是一个分类簇中的) |
| 伯努利分布
| 概率p | 贝塔分布
| 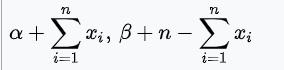 |
| 二项分布
| 概率p | 贝塔分布
| 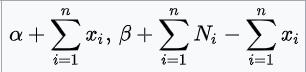 |
| 泊松分布
| λ | 伽马分布
| 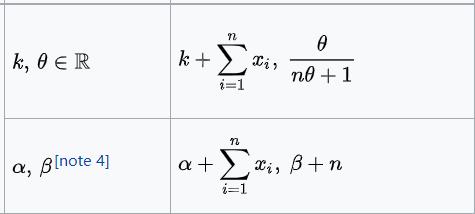 |
| 分类分布
| p | 迪利克雷分布
|  |
| 多分类分布
| p | 迪利克雷分布
| 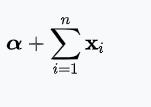 |
3.2 连续密度函数
| 概率分布函数 | 关于哪个参数的共轭先验分布 | 共轭先验分布的概率分布函数 | 后验分布的参数(后验分布和先验分布是一个分类簇中的) |
| 正态分布(已知标准差σ的情况下)
| 均值μ | 正态分布 | 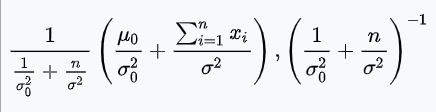 |
正态分布(已知精度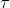 【方差的倒数】的情况下) 【方差的倒数】的情况下) | 均值μ | 正态分布 |
|
| 正态分布(已知均值μ的情况下) | 方差σ^2 | 逆伽马分布
| 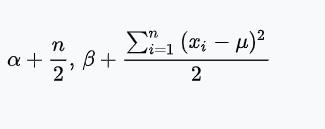 |
| 正态分布(已知均值μ的情况下) | 精度τ | 伽马分布(这里看α、β那一组)
| 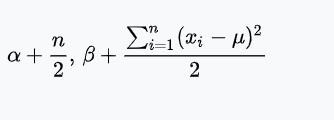 |
| 正态分布 | μ和σ^2 | 标准逆伽马分布
| 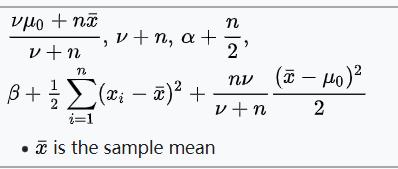 |
| 多元正态分布(已知协方差矩阵Σ的情况下) | 均值向量μ | 多元正态分布 | 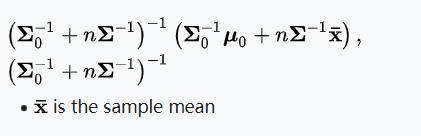 |
多元正态分布(已知精度矩阵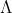 的情况下) 的情况下) | 均值向量μ | 多元正态分布 | 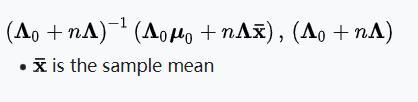 |
| 多元正态分布(已知均值向量μ的情况下) | 协方差矩阵Σ | 逆威沙特分布
| 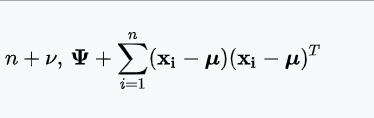 |
| 多元正态分布(已知均值向量μ的情况下) | 精度矩阵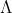 | 威沙特分布
|  |
| 多元正态分布 | μ和Σ | 高斯逆威沙特分布
| 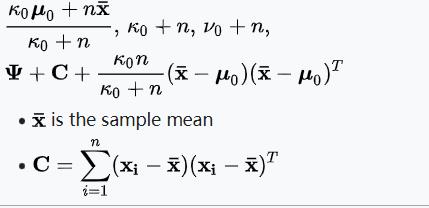 |
| 多元正态分布 | μ和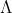 | 高斯威沙特分布
| 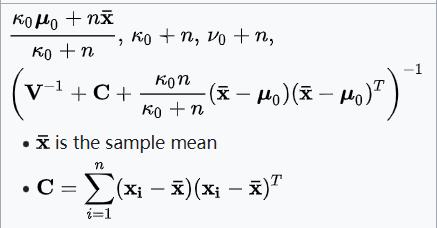 |
以上是关于概率统计笔记:共轭分布的主要内容,如果未能解决你的问题,请参考以下文章