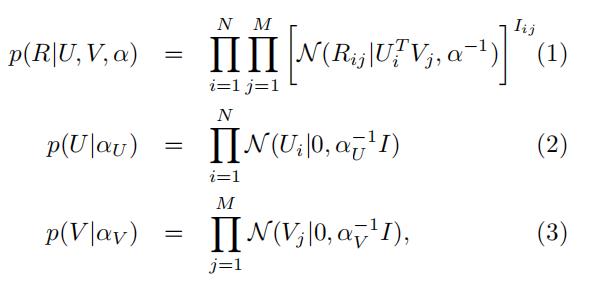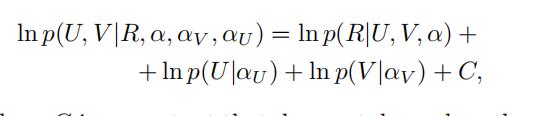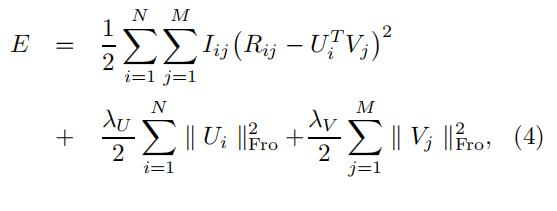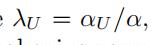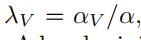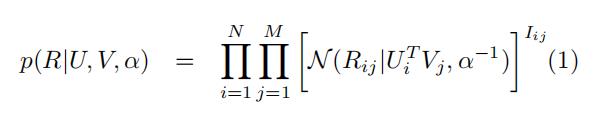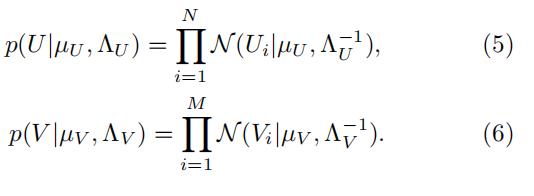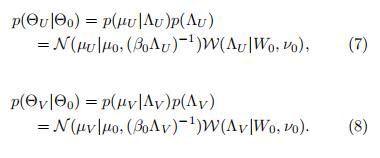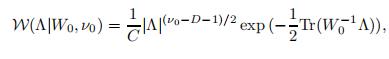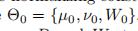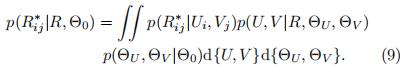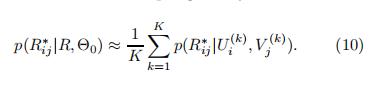论文笔记 Bayesian Probabilistic Matrix Factorizationusing Markov Chain Monte Carlo （ICML 2008）

Posted 2021-11-09 UQI-LIUWJ

0 摘要

        低秩矩阵逼近方法是协同过滤中最简单、最有效的方法之一。这类模型通常通过寻找模型参数的MAP估计来拟合数据，这一过程即使在非常大的数据集上也能有效地执行。

        然而，除非正则化参数被仔细地调整，否则这种方法很容易过度拟合，因为它找到了参数的单点估计。

        本文给出了概率矩阵分解(PMF)模型的完全贝叶斯处理方法，该方法通过对所有模型参数和超参数进行整合使用来自动控制模型容量。

        我们表明，贝叶斯PMF模型可以有效地训练使用马尔可夫链蒙特卡罗方法，将其应用到Netflix数据集，其中包含超过1亿电影评级。所得模型的预测精度明显高于使用MAP估计训练的PMF模型。

1 introduction

        N个用户对M部电影的N ×M偏好评分矩阵，是由一个D× N的用户系数矩阵U和D×M的因子矩阵V的乘积建模而成的。训练这样的模型相当于在给定的损失函数下找到观测到的N × M目标矩阵R的最佳近似。（使得U和V的乘积接近R）

        在实践中，我们通常对预测新用户/电影对的评级感兴趣，而不是估计模型参数。这个观点建议采用贝叶斯方法来解决涉及到整合模型参数的问题。在本文中，我们描述了一个完全贝叶斯处理的概率矩阵分解(PMF)模型。

        我们模型的特点是在该模型中使用了马尔可夫链蒙特卡罗(MCMC)方法进行近似推理。在实践中，MCMC方法很少用于大规模的问题，因为实践者认为它们非常慢。在本文中，我们证明MCMC可以成功地应用于大型、稀疏和非常不平衡的Netflix数据集，该数据集包含超过1亿用户/电影评级。

        我们还表明，与使用MAP训练的标准PMF模型相比，它显著提高了模型的预测精度，特别是对于不经常使用的用户。（使用MAP的PMF模型，它的正则化参数需要在验证集上经过仔细调整。）

2 PMF （Probabilistic Matrix Factorization）

线性代数笔记：概率矩阵分解 Probabilistic Matrix Factorization （PMF）_UQI-LIUWJ的博客-CSDN博客_pmf模型

 PMF的假设条件：

 其中表示均值为μ，精度（协方差矩阵的倒数）为α的高斯分布

 表示示性函数，当用户i对电影j有打分的时候，就是1

        在这个模型中，学习是通过在固定超参数的电影特征和用户特征的前提下，最大化对数后验来实现的

         

         最大化对数后验概率 等价于最小化如下的损失函数：

 

其中：

 

表示Frobenius 范数，见线性代数笔记：Frobenius 范数_UQI-LIUWJ的博客-CSDN博客）

         这种训练过程的主要缺点是需要手动的复杂性控制，这对于使模型很好地泛化至关重要，特别是在稀疏和不平衡的数据集上。

        控制模型复杂度的一种方法是寻找合适的正则化参数λU和λV的值。例如，我们可以考虑一组合理的参数值，针对每个参数设置训练一个模型，并选择在验证集上表现最好的模型。然而，这种方法在计算上非常昂贵，因为它需要训练大量模型，而不是单个模型。

        我们可以为超参数引入先验，并在参数和超参数上最大化模型的对数后验，从而允许基于训练数据自动控制模型的复杂性 。

        在下一节中，我们将描述使用MCMC方法集成模型参数和超参数的PMF模型的完全贝叶斯处理，它提供了完全自动的复杂性控制。

3 BPMF （Bayesian Probabilistic Matrix Factorization）

3.1 模型

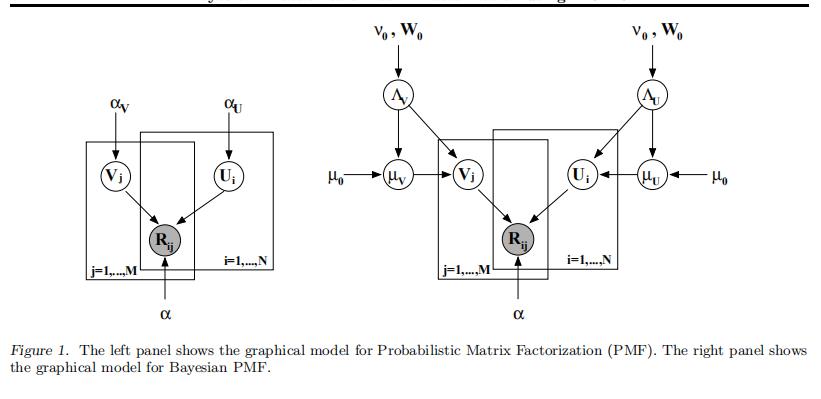
BPMF的图像化模型是由下图（右）展示的【下图（左）是PMF的图，以作对比】：

和PMF一样 观测打分矩阵的概率分布也是如式(1)所示

 用户特征矩阵和打分特征矩阵的先验如下：

  对于用户特征和电影打分特征的超参数和，它们满足如下的高斯威沙特分布 概率统计笔记：高斯威沙特分布_UQI-LIUWJ的博客-CSDN博客

        

W是有着v0自由度，D×D维度协方差矩阵的威沙特分布，它的概率分布如下：

 其中C是正则化长度。为了方便起见，我们令

在我们的实验中，我们令v0=D，W0=I，μ0=0 

 3.2 预测

        预测的打分矩阵R*的概率分布如下：

 

         由于后验的复杂性，准确评估这种预测分布在分析上是难以处理的，我们需要诉诸于近似推断。

         我们这里使用MCMC来进行近似

        

          其中，样本由一个马尔可夫链生成，这个马尔可夫链的平稳分布是模型参数和超参数（）的后验分布。

        基于蒙特卡罗的方法的优点是它们在渐近中产生精确的结果。然而，在实践中，MCMC方法通常计算量较大，因此它们的使用仅限于小规模问题。

 3.3 推断 

 

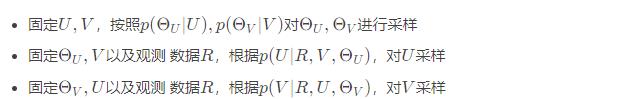
每完成这样一轮，称为一个Epoch。随着epoch增加，生成的预测矩阵R的分布逐渐准确。

...............................................................................................................

 3.3.1 采样θU

  

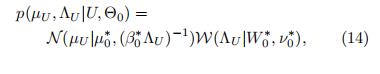
 从一个高斯威沙特分布里面提取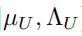

 其中

 

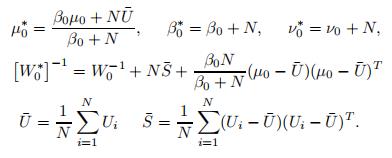
 推导过程如下：

BPMF论文辅助笔记： 固定U，更新θU 部分推导_UQI-LIUWJ的博客-CSDN博客

3.3.2 采样θV

和3.3.1 类似，只不过N 换成M，U换成V

3.3.3  固定R，θU，V，采样Ui

（在论文中，α设置为2）

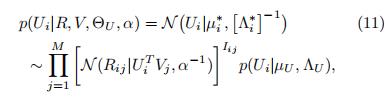
从一个高斯分布里面采样Ui

其中

 

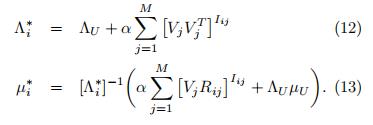
推导过程如下： BPMF论文辅助笔记：采样Ui 部分推导_UQI-LIUWJ的博客-CSDN博客

3.3.4 固定R，θV，U，采样Vi

和3.3.3 类似，只不过V换成U，M换成N

4 实验部分

4.1 数据集

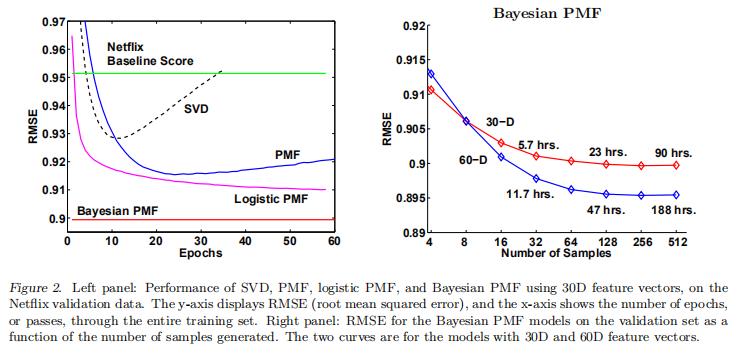
        Netflix收集的数据代表了Netflix在1998年10月至2005年12月间获得的所有收视率的分布。

        训练数据集由480,189个随机选择的匿名用户对17,770个电影标题的100,480,507个评分组成。（如果每个人都看完了所有的电影的话，理论上是8,532,958,530对用户-电影对）作为训练数据的一部分，Netflix还提供了包含1408395个验证数据。

        此外，Netflix还提供了一个包含2817131对用户/电影对的测试集，不提供评分。这些用户/电影对是从训练数据集中的用户子集中最近的评分中选择的。通过向Netflix提交预测的评分，然后发布测试集未知部分的均方根误差(RMSE)来评估性能。

        作为基准，Netflix提供了基于相同数据训练的自己系统的测试分数0.9514。

 注：左图中BPMF不是一条平行于x轴的直线，而是斜率很缓的向下斜线