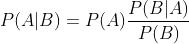概率统计笔记：贝叶斯推断 Bayesian Inference

Posted 2021-11-22 UQI-LIUWJ

1 贝叶斯定理和全概率公式（复习）

贝叶斯定理（条件概率的计算公式）：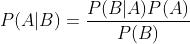

全概率公式：如果A和A'构成了样本空间的一个划分，那么事件B的概率为：

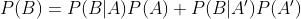
全概率公式下条件概率的另一种写法：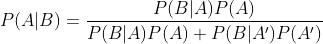

2 贝叶斯推断

        对条件概率公式进行变形，可以得到如下形式：

                ​​​​​​​        

        P(A)——先验概率（prior probability）【事件B发生之前，事件A概率的一个判断】

        P(A|B)——后验概率（posterior probability）【事件B发生后，对事件A概率的一个重新判断】

        ——可能性函数（likelihood）【似然，调整因子，使得估计概率更接近真实概率】

        所以条件概率可以表示为：

        后验概率=先验概率 × 调整因子

         这就是贝叶斯推断的含义。我们先预估一个"先验概率"，然后加入实验结果，看这个实验到底是增强还是削弱了"先验概率"，由此得到更接近事实的"后验概率"。

• 如果"可能性函数"大于1，意味着"先验概率"被增强，事件A的发生的可能性变大

•  如果"可能性函数"等于1，意味着B事件无助于判断事件A的可能性

•  如果"可能性函数"小于1，意味着"先验概率"被削弱，事件A的可能性变小

        

 参考资料：浅谈贝叶斯推断 - 加拿大小哥哥 - 博客园 (cnblogs.com)