置换群，Polya引理和burnside引理（等价类计数问题）

Posted 2021-11-04 Jozky86

参考文章：
等价类计数问题
Burnside引理&Pólya定理
Burnside引理与Polya定理
置换群和Burnside引理，Polya定理

概念引入：

离散数学应该学过置换群的相关概念，置换本质就是映射，可以理解成一个正方形绕其中心逆时针旋转90度，就可以看作是正方形四个顶点的置换。
置换会形成一个环。且如果一个状态经过置换后跟原来相同，可以认为该状态为f的不动点。
有些题目中经常出现”本质不同的方案数“，一般是指等价类的数目，题目定义一个等价关系，满足等价关系的元素属于同一等价类。等价关系通常是一个置换集合F，如果一个置换能把其中一个方案映射到另一个方案中，就认为两者是等价的。

题目引入：

问题描述

一个由2*2方格组成的正方形，每个格子上可以涂色或不涂色，问共有多少种本质不同的涂色方案。
（若两种方案可通过旋转互相得到，称作本质相同的方案）

解法：

先看一共有多少方案，不考虑本质不同，一共16种

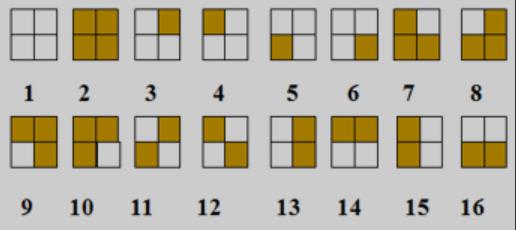
现在我们开始将本质相同的方案合并归类：
方案1：{1}
方案2：{2}
方案3：{3，4，5，6}
方案4：{7，8，9，10}
方案5：{11，12}
方案6：{13，14，15，16}
一共六种不同的方案
这里结合我们上面说的，旋转可以看作是置换，所有置换组成置换群。
如果x通过置换(旋转)得到y，说明x和y等价。
与x互相等价的一组元素组成一个集合，称为x的等价类。
不动元为旋转一定角度，图形不发生改变

在这个问题中，我们要求的就是有多少个等价类？
我们引入一个引理：burnside引理
burnside引理：
$$|X/G|=|G{|}^{-1}\cdot \sum _{g\in G}|x^g|$$
等价类的个数 = 每个置换中不动元的个数和 ➗置换群的大小
我们统计不动元的个数
不旋转（逆时针360度）：不动元16个
逆时针90度，不动元2个{1,2}
逆时针180度，不动元4个{1,2,11,12}
逆时针270度，不动元2个{1,2}
置换群大小为4
$$|X/G|=\frac{16+2+4+2}{4}$$

Burnside’s引理：

$$|X/G|=|G{|}^{-1}\cdot \sum _{g\in G}|x^g|$$
等价类的个数 = 每个置换中不动元的个数和 ➗置换群的大小
等价类的个数=不动元个数的平均数

Pólya引理：

$$|\frac{Y^X}{G}|=\frac{1}{|G|}\sum _{g\in G}|Y{|}^{c(g)}$$
$$染色方案数(等价类个数)=\frac{1}{珠子数(总置换数)}\sum _{对于每种置换}颜色数(映射数{)}^{循环节数}$$