图--06---加权有向图最短路径Dijstra算法
Posted 高高for 循环
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了图--06---加权有向图最短路径Dijstra算法相关的知识,希望对你有一定的参考价值。
文章目录
加权有向图
- 之前学习的加权无向图中,边是没有方向的,并且同一条边会同时出现在该边的两个顶点的邻接表中,为了能够处理含有方向性的图的问题,我们需要实现以下加权有向图。
加权有向图—边的表示
1. API设计:
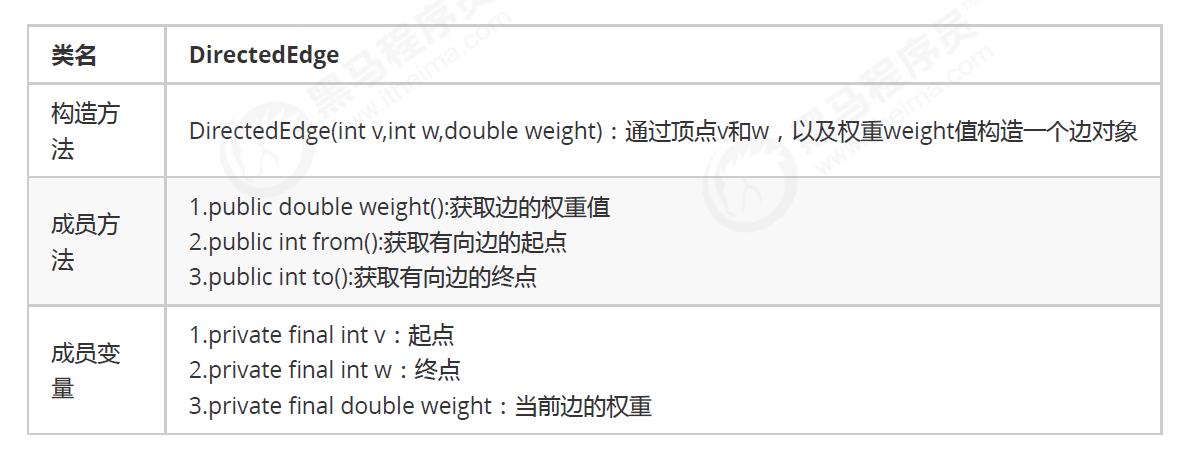
2. 代码:
public class DirectedEdge {
private final int v;//起点
private final int w;//终点
private final double weight;//当前边的权重
//通过顶点v和w,以及权重weight值构造一个边对象
public DirectedEdge(int v, int w, double weight) {
this.v = v;
this.w = w;
this.weight = weight;
}
//获取边的权重值
public double weight(){
return weight;
}
//获取有向边的起点
public int from(){
return v;
}
//获取有向边的终点
public int to(){
return w;
}
}
加权有向图----图的实现
1. API设计:

2. 代码:
package graph.tu;
import java.util.Queue;
import java.util.concurrent.ConcurrentLinkedDeque;
import java.util.concurrent.ConcurrentLinkedQueue;
public class EdgeWeightedDigraph {
//顶点总数
private final int V;
//边的总数
private int E;
//邻接表
private Queue<DirectedEdge>[] adj;
//创建一个含有V个顶点的空加权有向图
public EdgeWeightedDigraph(int V) {
//初始化顶点数量
this.V = V;
//初始化边的数量
this.E = 0;
//初始化邻接表
this.adj = new Queue[V];
for (int i = 0; i < adj.length; i++) {
adj[i] = new ConcurrentLinkedDeque<DirectedEdge>();
}
}
//获取图中顶点的数量
public int V() {
return V;
}
//获取图中边的数量
public int E() {
return E;
}
//向加权有向图中添加一条边e
public void addEdge(DirectedEdge e) {
//边e是有方向的,所以只需要让e出现在起点的邻接表中即可
int v = e.from();
adj[v].offer(e);
E++;
}
//获取由顶点v指出的所有的边
public Queue<DirectedEdge> adj(int v) {
return adj[v];
}
//获取加权有向图的所有边
public Queue<DirectedEdge> edges() {
//遍历图中的每一个顶点,得到该顶点的邻接表,遍历得到每一条边,添加到队列中返回即可
Queue<DirectedEdge> allEdges = new ConcurrentLinkedQueue<>();
for (int v = 0;v<V;v++){
for (DirectedEdge edge : adj[v]) {
allEdges.offer(edge);
}
}
return allEdges;
}
}
最短路径
- 有了加权有向图之后,我们立刻就能联想到实际生活中的使用场景,例如在一副地图中,找到顶点a与地点b之间的路径,这条路径可以是距离最短,也可以是时间最短,也可以是费用最小等,如果我们把
距离/时间/费用看做是成本,那么就需要找到地点a和地点b之间成本最小的路径,也就是我们接下来要解决的最短路径问题。
定义:
在一副加权有向图中,从顶点s到顶点t的最短路径是所有从顶点s到顶点t的路径中总权重最小的那条路径。
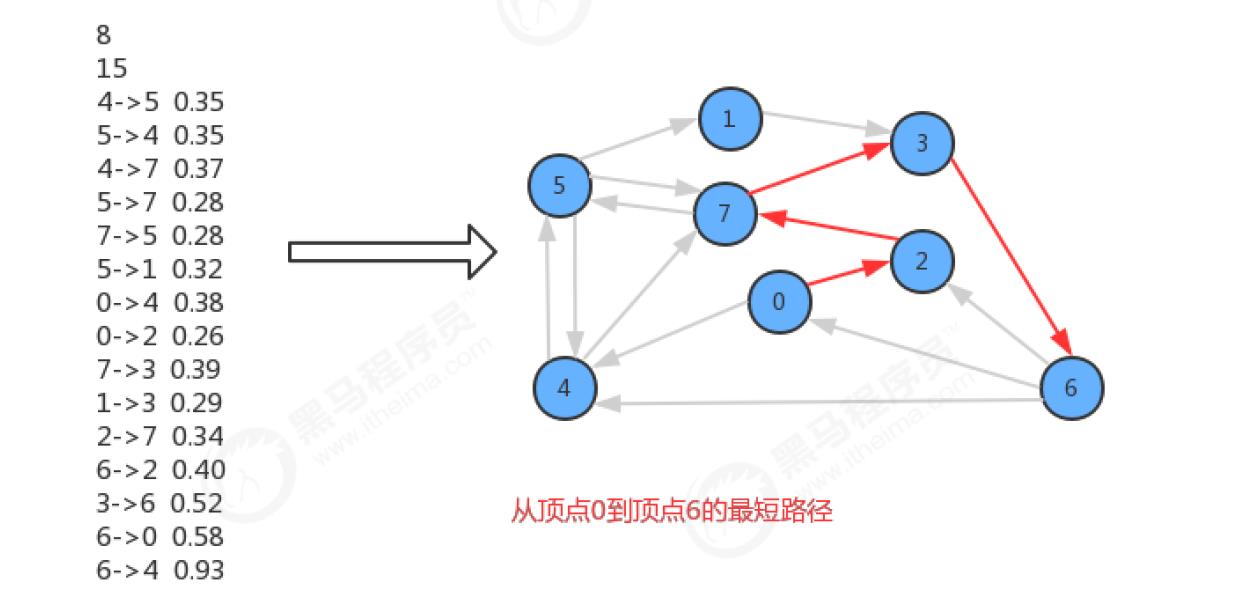
性质:
- 路径具有方向性;
- 权重不一定等价于距离。权重可以是距离、时间、花费等内容,权重最小指的是成本最低
- 只考虑连通图。一副图中并不是所有的顶点都是可达的,如果s和t不可达,那么它们之间也就不存在最短路径,为了简化问题,这里只考虑连通图。
- 最短路径不一定是唯一的。从一个顶点到达另外一个顶点的权重最小的路径可能会有很多条,这里只需要找出一条即可。
最短路径树:
- 给定一副加权有向图和一个顶点s,以s为起点的一棵最短路径树是图的一副子图,它包含顶点s以及从s可达的所有顶点。这棵有向树的根结点为s,树的每条路径都是有向图中的一条最短路径。
最短路径树API设计

松弛技术
- 松弛这个词来源于生活:一条橡皮筋沿着两个顶点的某条路径紧紧展开,如果这两个顶点之间的路径不止一条,还有存在更短的路径,那么把皮筋转移到更短的路径上,皮筋就可以放松了。
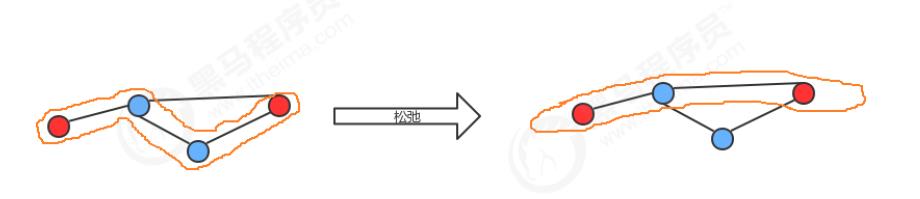
松弛这种简单的原理刚好可以用来计算最短路径树。
在我们的API中,需要用到两个成员变量edgeTo和distTo,分别存储边和权重。一开始给定一幅图G和顶点s,我们只知道图的边以及这些边的权重,其他的一无所知,此时初始化顶点s到顶点s的最短路径的总权重disto[s]=0;顶点s到其他顶点的总权重默认为无穷大,随着算法的执行,不断的使用松弛技术处理图的边和顶点,并按一定的条件更新edgeTo和distTo中的数据,最终就可以得到最短路劲树。
边的松弛:
放松边v->w意味着检查从s到w的最短路径是否先从s到v,然后再从v到w?
- 如果是,则v-w这条边需要加入到最短路径树中,更新edgeTo和distTo中的内容:edgeTo[w]=表示v->w这条边的DirectedEdge对象,distTo[w]=distTo[v]+v->w这条边的权重;
- 如果不是,则忽略v->w这条边。
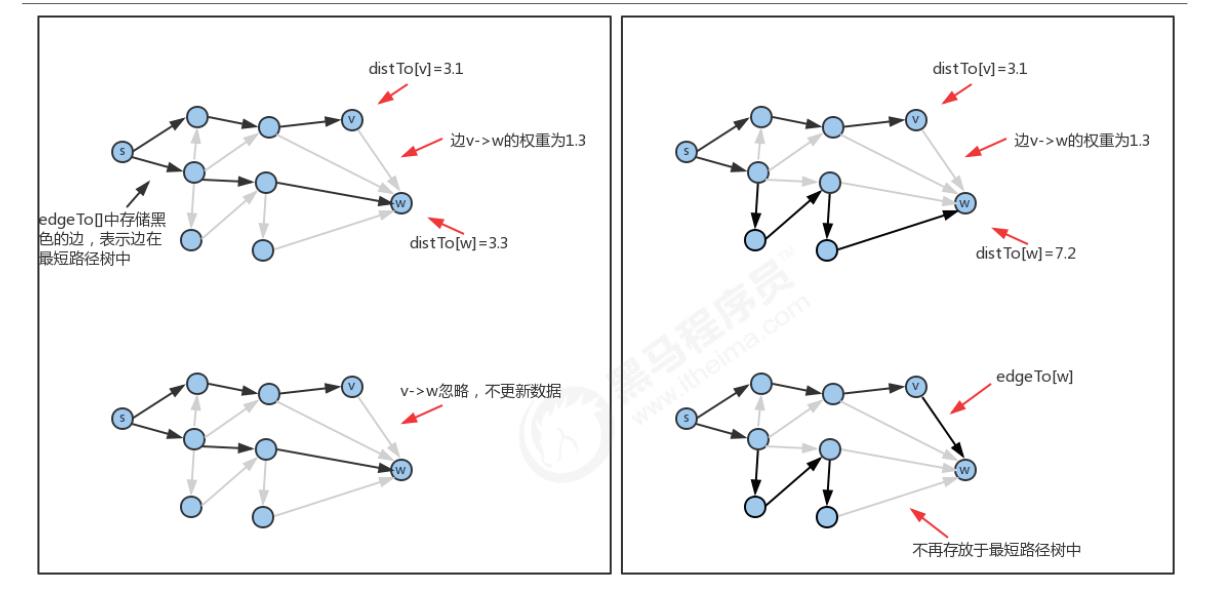
顶点的松弛:
顶点的松弛是基于边的松弛完成的,只需要把某个顶点指出的所有边松弛,那么该顶点就松弛完毕。例如要松弛顶点v,只需要遍历v的邻接表,把每一条边都松弛,那么顶点v就松弛了。
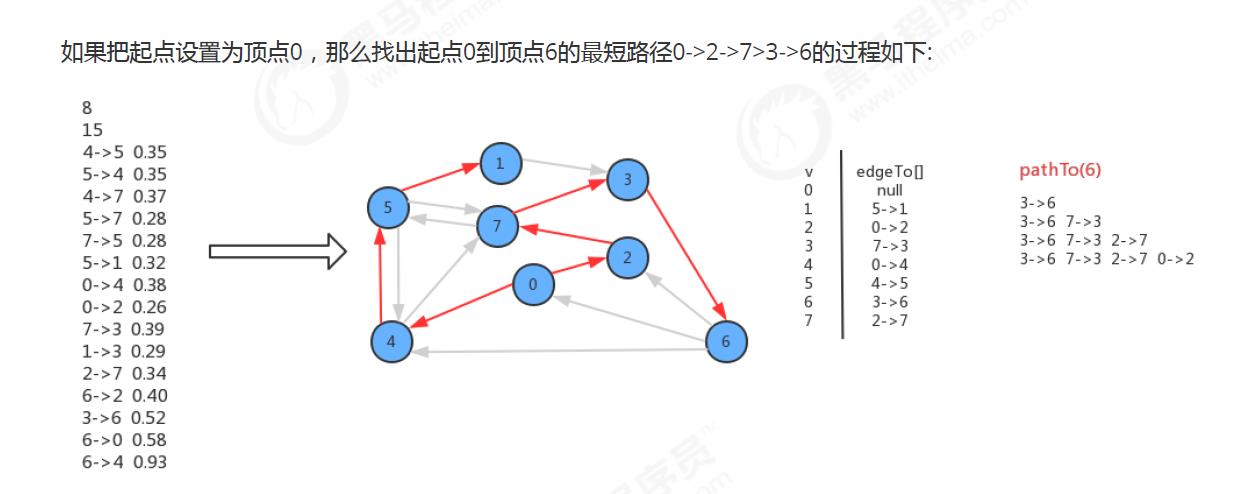
Dijstra算法实现
Disjstra算法的实现和Prim算法很类似,构造最短路径树的每一步都是向这棵树中添加一条新的边,而这条新的边是有效横切边pq队列中的权重最小的边。
辅助类:
1. DirectedEdge----加权有向边
2. EdgeWeightedDigraph----加权有向图
3. IndexMinPriorityQueue----最小优先队列
package graph.tu;
public class IndexMinPriorityQueue<T extends Comparable<T>> {
//存储堆中的元素
private T[] items;
//保存每个元素在items数组中的索引,pq数组需要堆有序
private int[] pq;
//保存qp的逆序,pq的值作为索引,pq的索引作为值
private int[] qp;
//记录堆中元素的个数
private int N;
public IndexMinPriorityQueue(int capacity) {
this.items = (T[]) new Comparable[capacity+1];
this.pq = new int[capacity+1];
this.qp= new int[capacity+1];
this.N = 0;
//默认情况下,队列中没有存储任何数据,让qp中的元素都为-1;
for (int i = 0; i < qp.length; i++) {
qp[i]=-1;
}
}
//获取队列中元素的个数
public int size() {
return N;
}
//判断队列是否为空
public boolean isEmpty() {
return N==0;
}
//判断堆中索引i处的元素是否小于索引j处的元素
private boolean less(int i, int j) {
return items[pq[i]].compareTo(items[pq[j]])<0;
}
//交换堆中i索引和j索引处的值
private void exch(int i, int j) {
//交换pq中的数据
int tmp = pq[i];
pq[i] = pq[j];
pq[j] = tmp;
//更新qp中的数据
qp[pq[i]]=i;
qp[pq[j]] =j;
}
//判断k对应的元素是否存在
public boolean contains(int k) {
return qp[k] !=-1;
}
//最小元素关联的索引
public int minIndex() {
return pq[1];
}
//往队列中插入一个元素,并关联索引i
public void insert(int i, T t) {
//判断i是否已经被关联,如果已经被关联,则不让插入
if (contains(i)){
return;
}
//元素个数+1
N++;
//把数据存储到items对应的i位置处
items[i] = t;
//把i存储到pq中
pq[N] = i;
//通过qp来记录pq中的i
qp[i]=N;
//通过堆上浮完成堆的调整
swim(N);
}
//删除队列中最小的元素,并返回该元素关联的索引
public int delMin() {
//获取最小元素关联的索引
int minIndex = pq[1];
//交换pq中索引1处和最大索引处的元素
exch(1,N);
//删除qp中对应的内容
qp[pq[N]] = -1;
//删除pq最大索引处的内容
pq[N]=-1;
//删除items中对应的内容
items[minIndex] = null;
//元素个数-1
N--;
//下沉调整
sink(1);
return minIndex;
}
//删除索引i关联的元素
public void delete(int i) {
//找到i在pq中的索引
int k = qp[i];
//交换pq中索引k处的值和索引N处的值
exch(k,N);
//删除qp中的内容
qp[pq[N]] = -1;
//删除pq中的内容
pq[N]=-1;
//删除items中的内容
items[k]=null;
//元素的数量-1
N--;
//堆的调整
sink(k);
swim(k);
}
//把与索引i关联的元素修改为为t
public void changeItem(int i, T t) {
//修改items数组中i位置的元素为t
items[i] = t;
//找到i在pq中出现的位置
int k = qp[i];
//堆调整
sink(k);
swim(k);
}
//使用上浮算法,使索引k处的元素能在堆中处于一个正确的位置
private void swim(int k) {
while(k>1){
if (less(k,k/2)){
exch(k,k/2);
}
k = k/2;
}
}
//使用下沉算法,使索引k处的元素能在堆中处于一个正确的位置
private void sink(int k) {
while(2*k<=N){
//找到子结点中的较小值
int min;
if (2*k+1<=N){
if (less(2*k,2*k+1)){
min = 2*k;
}else{
min = 2*k+1;
}
}else{
min = 2*k;
}
//比较当前结点和较小值
if (less(k,min)){
break;
}
exch(k,min);
k = min;
}
}
}
Dijstra算法代码
package graph.tu;
import java.util.Queue;
import java.util.concurrent.ConcurrentLinkedQueue;
public class DijkstraSP {
//索引代表顶点,值表示从顶点s到当前顶点的最短路径上的最后一条边
private DirectedEdge[] edgeTo;
//索引代表顶点,值从顶点s到当前顶点的最短路径的总权重
private double[] distTo;
//存放树中顶点与非树中顶点之间的有效横切边
private IndexMinPriorityQueue<Double> pq;
//根据一副加权有向图G和顶点s,创建一个计算顶点为s的最短路径树对象
public DijkstraSP(EdgeWeightedDigraph G, int s){
//初始化edgeTo
this.edgeTo = new DirectedEdge[G.V()];
//初始化distTo
this.distTo = new double[G.V()];
for (int i = 0; i < distTo.length; i++) {
distTo[i] = Double.POSITIVE_INFINITY;
}
//初始化pq
this.pq = new IndexMinPriorityQueue<>(G.V());
//找到图G中以顶点s为起点的最短路径树
//默认让顶点s进入到最短路径树中
distTo[s] = 0.0;
pq.insert(s,0.0);
//遍历pq
while(!pq.isEmpty()){
relax(G,pq.delMin());
}
}
//松弛图G中的顶点v
private void relax(EdgeWeightedDigraph G, int v){
for (DirectedEdge edge : G.adj(v)) {
//获取到该边的终点w
int w = edge.to();
//通过松弛技术,判断从起点s到顶点w的最短路径是否需要先从顶点s到顶点v,然后再由顶点v到顶点w
if (distTo(v)+edge.weight()<distTo(w)){
distTo[w] = distTo[v]+edge.weight();
edgeTo[w] = edge;
//判断pq中是否已经存在顶点w,如果存在,则更新权重,如果不存在,则直接添加
if (pq.contains(w)){
pq.changeItem(w,distTo(w));
}else{
pq.insert(w,distTo(w));
}
}
}
}
//获取从顶点s到顶点v的最短路径的总权重
public double distTo(int v){
return distTo[v];
}
//判断从顶点s到顶点v是否可达
public boolean hasPathTo(int v){
return distTo[v]<Double.POSITIVE_INFINITY;
}
//查询从起点s到顶点v的最短路径中所有的边
public Queue<DirectedEdge> pathTo(int v){
//判断从顶点s到顶点v是否可达,如果不可达,直接返回null
if (!hasPathTo(v)){
return null;
}
//创建队列对象
Queue<DirectedEdge> allEdges = new ConcurrentLinkedQueue<>();
while (true){
DirectedEdge e = edgeTo[v];
if (e==null){
break;
}
allEdges.offer(e);
v = e.from();
}
return allEdges;
}
}
测试:
查找最短路径,0->6的最短路径
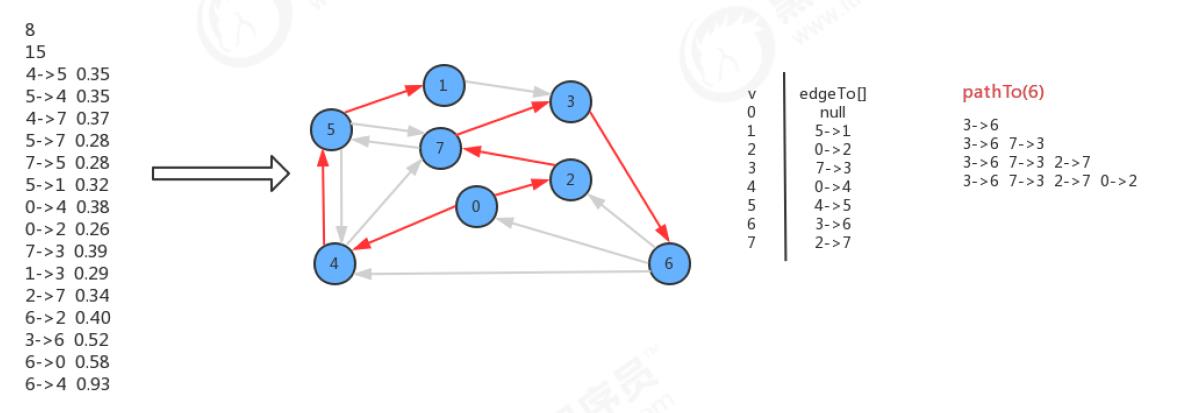
package graph.tu;
import java.io.BufferedReader;
import 以上是关于图--06---加权有向图最短路径Dijstra算法的主要内容,如果未能解决你的问题,请参考以下文章