一维数组寻找两个数字之和为N的组合
Posted 娃都会打酱油了
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了一维数组寻找两个数字之和为N的组合相关的知识,希望对你有一定的参考价值。
问题是这样的,一维数组,包含不重复的数字,求两个数相加之和为N的所有组合。
笛卡尔乘积方式
public static void Addition2WithCartesian(HashSet<int> hash, int sum)
{
Console.WriteLine("通过笛卡尔乘积进行计算2个数字组合(不允许重复)");
Console.WriteLine("数据源:" + string.Join(" ", hash));
var query = (from a in hash
from b in hash
where a + b == sum && a != b
select a < b ? $"{a} + {b}" : $"{b} + {a}").Distinct();
if (!query.Any())
{
Console.WriteLine("没有符合相加结果为{0}的数字组合", sum);
}
else
{
Console.WriteLine("两个数字相加为{0}的组合如下", sum);
foreach (var tmp in query)
{
Console.WriteLine(tmp);
}
}
}
这种方式虽然能出结果,但明显不是对方期望的结果,要求其它方式
遍历HashSet方式
public static void Addition2WithNormal(HashSet<int> hash, int sum)
{
Console.WriteLine("HashSet计算2个数字组合");
Console.WriteLine("数据源:" + string.Join(" ", hash));
while (hash.Count > 1)
{
var number = hash.First();
hash.Remove(number);
var needNumber = sum - number;
if (hash.Contains(needNumber))
{
hash.Remove(needNumber);
Console.WriteLine($"{number} + {needNumber} = {sum}");
}
}//O(n)
}
通过空间换时间,这里直接用HashSet<T>作为数组源,当集合剩余数字只有一个时,就可以结束循环,所以此时只需循环N-1次,时间复杂度是O(n)
出题方有些不开心,追问那现在数组变了,可以存在重复的数字,每个数字只能用一次,这时候如何获取所有的组合?
传统的两层循环方式
public static void Addition2Slowest(List<int> source, int sum)
{
Console.WriteLine("两层循环计算2个数字组合(允许存在重复数字)");
Console.WriteLine("数据源:" + string.Join(" ", source));
for (var i = 0; i < source.Count - 1; i++)
{
for (var j = 1; j < source.Count; j++)
{
if (source[i] + source[j] == sum)
{
Console.WriteLine($"{source[i]} + {source[j]} = {sum}");
source.RemoveAt(j);
source.RemoveAt(i);
i--;
break;
}
}
}//O(n^2) 最小O(n)
}
好吧,因为要移除已匹配的数字,所以不能用Array,好家伙,占了空间不说,时间复杂度也没少为O(n^2)
PS:用Array其实也可以,RemoveAt调整为设置数字值为null,循环时多一次null判断
遍历Dictionary方式
public static void Addition2RepeatWithNormal(IEnumerable<int> source, int sum)
{
//C#内置集合类的时间复杂度 https://www.cnblogs.com/wccfsdn/p/11945454.html
Console.WriteLine("Dictionary计算2个数字组合(允许存在重复数字)");
Console.WriteLine("数据源:" + string.Join(" ", source));
//GroupBy O(n) ToDictionary O(n) 也可以自行for循环 O(n)
var dic = source.GroupBy(_ => _).ToDictionary(k => k.Key, v => v.Count());
while (dic.Count > 0)//必须是0,避免出现sum是偶数,数据源中存在重复的sum/2数字
{
var number = dic.First().Key;//遍历是O(n),First是O(1)
CheckKey(number);
var needNumber = sum - number;
if (dic.ContainsKey(needNumber))
{
CheckKey(needNumber);
Console.WriteLine($"{number} + {needNumber} = {sum}");
}
}//O(n)
void CheckKey(int key)
{
dic[key]--; //O(1)
if (dic[key] == 0) //O(1)
{
dic.Remove(key); //O(1)
}
}
}
本质其实与HashSet<T>方式并没有太大差异,只是由直接HashSet<T>.Remove,变成了需要先判断下是否还有可用数字,只有数字数量为0时才执行Remove,当然时间复杂度也还是O(n)
排序后双指针方式
public static void Addition2RepeatWithDoublePointer(IEnumerable<int> source, int sum)
{
//排序的时间复杂度影响整个组合的时间复杂度
var tmpList = source.OrderBy(_ => _).ToList();
Console.WriteLine("双指针方式计算2个数字组合(允许存在重复数字)");
Console.WriteLine("排序后的数据源:" + string.Join(" ", tmpList));
int i = 0, j = tmpList.Count - 1;
while (i < j)
{
while (j > i)
{
var tmpSum = tmpList[i] + tmpList[j];
if (tmpSum <= sum)
{
if (tmpSum == sum)
{
Console.WriteLine($"{tmpList[i]} + {tmpList[j]} = {sum}");
j--;
}
//两数之和小于sum时,应当停止循环,且不更改指针
break;
}
j--;
}
i++;
}
}
这种方式虽然看起来有两层循环,但其实每个数字都只能被循环到一次,所以其时间复杂度还是为O(n)
测试上面的所有方式
var hash = Enumerable.Range(-5, 15).ToHashSet();
var repeatSource = Enumerable.Range(-7, 12).ToList();
repeatSource.AddRange(hash);//构建重复数据
var sum = 6;
Addition2WithCartesian(hash, sum);
Console.WriteLine();
Addition2Slowest(repeatSource.ToList(), sum);
Console.WriteLine();
Addition2WithNormal(hash, sum);
Console.WriteLine();
Addition2RepeatWithNormal(repeatSource, sum);
Console.WriteLine();
Addition2RepeatWithDoublePointer(repeatSource, sum);
执行结果如下
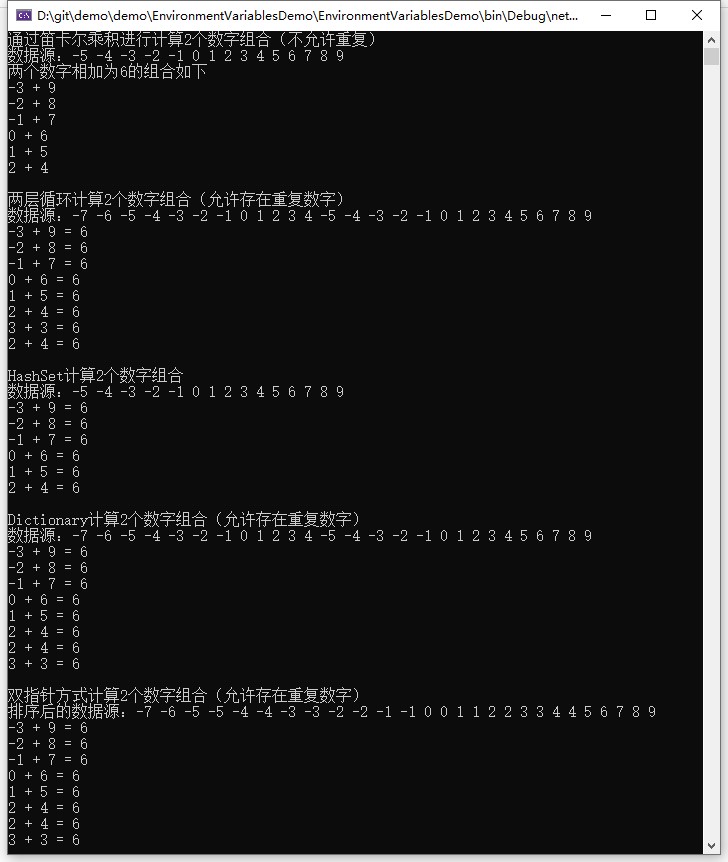
以上是关于一维数组寻找两个数字之和为N的组合的主要内容,如果未能解决你的问题,请参考以下文章