八大排序算法

Posted 2021-10-26 两片空白

目录

前言：

一.排序概念

二.常见的排序算法

        2.1 插入排序

         2.1.1 直接插入排序       

        2.1.2 希尔排序

        2.2 选择排序

        2.2.1 直接选择排序

        2.2.2 堆排序

        2.3 交换排序

        2.3.1 冒泡排序

         2.3.2 快速排序

        2.4归并排序

  2.5 计数排序

---

前言：

        为了方便复习，重新总结了一下排序。

一.排序概念

        排序：就是将一串数据，按照某个或者某些关键字的大小，按照递增或者递减减数据排列起来。

        稳定性：两相同的数据经过排序后，两数据的相对位置，相比较没排序之前的相对位置不变。比如：数据r[i] 和 r[j]。没排序之前r[i]在r[j]前面，记过排序算法排序后，r[i]还是在r[j]前面，则该排序算法是稳定的，否则是不稳定的。

        内部排序：数据元素放在内存中排序。

        外部排序：数据元素太多，不能同时放在内存中，根据排序过程的要求，在内外存之间引动数据的排序。

二.常见的排序算法

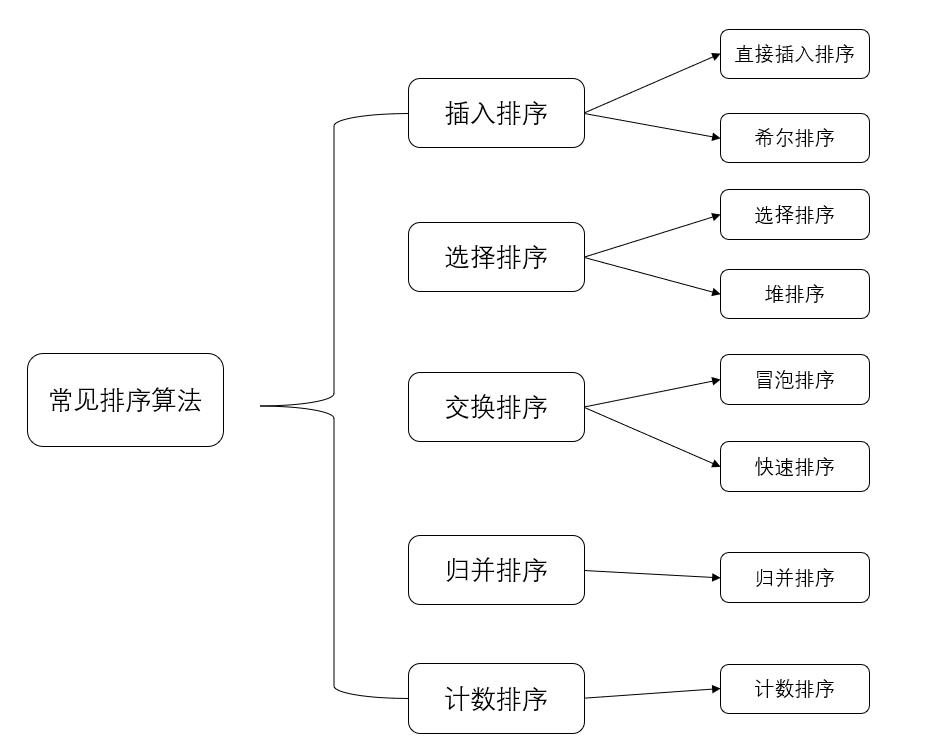
        2.1 插入排序

        原理：把待排序的数据按照关键码的大小，按照安排徐规则，将当前数据插入到已经排序好的数据中，使其称为一个新的排序好的数据，知道所有数据插完为止。

         2.1.1 直接插入排序       

        原理：当插入第i个元素时，前面的i-1个元素已经时有序的，此时用第i个元素的值和前面i-1个元素进行比较，直到找到插入位置，插入即可，原来位置的元素顺序后移。

         

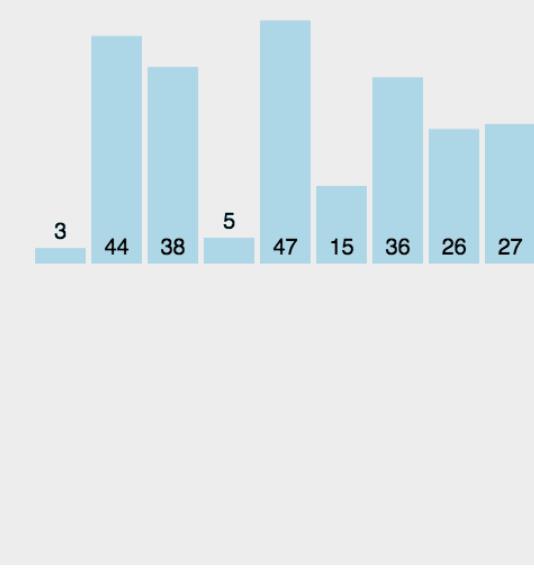
直接插入排序编写升序代码：如果想写降序，改变大小符号即可

1. 只有一个数据不需要排序
2. 从第二个数据开始，插入值不断和前面的数据进行比较，直到找到插入位置
3. 比较的同时需要将前面的值往后移
4. 找到插入位置，将数据插入即可。
5. 注意要保存插入的值，不然数据往后移时会改变插入值。

//升序
void InsertSort(int* a, int n){

	for (int i = 0; i<n - 1; i++){//到n-1，key是从end+1开始
		int end = i;
		//我们需要保存要插入的值，完后移的时候会改变原来的值
		int key = a[end + 1];
		//找插入位置
		while (end >= 0){
			//和前面值进行比较
			if (a[end] > key){
				a[end + 1] = a[end];
				end--;
			}
			else{
				//找到
				break;
			}
		}
		//插入
		a[end + 1] = key;
	}


}

       我们发现插入排序需要将数据不断的往后移。最坏的情况，要排升序，但是元素是降序的。随后的情况，要排升序，元素越接近升序。

时间复杂度：O(n^2)

空间复杂度：O(1)

稳定性：稳定，相同数据相对位置并不会发送改变。

        2.1.2 希尔排序

        希尔排序是对插入排序的优化，插入排序要排升序，但是元素是降序时，需要挪动数据的次数会很多。希尔排序就是将降序的数据，通过方法来使降序的数据，变成接近升序，来降低插入排序的次数。

 在博客希尔排序算法中，我有做详细介绍。

        2.2 选择排序

        原理：每次选择待排序数据区域中，最大(或者最小)的元素，与序列的起始位置进行交换，直到待排序的数据排完。

        2.2.1 直接选择排序

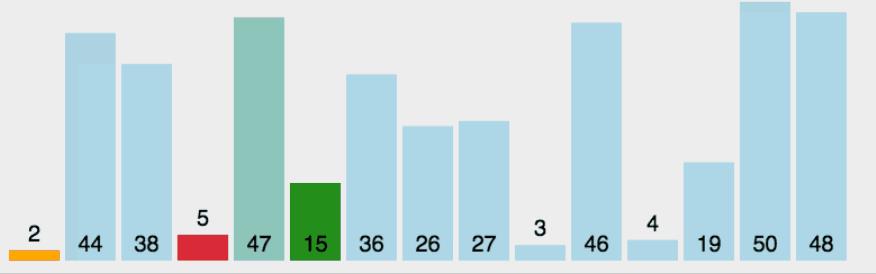
编码(升序)：

1.  在待排序元素中找到最小值
2. 如果不是开始位置，与开始位置进行值交换

//选择排序(一次选一个数)
void SelectSort(int* a, int n)
{
	for (int i = 0; i < n; i++){
		int min_t = a[i];//保存最小值
		int pos = i;//保存最小值下标
		for (int j = i; j < n; j++){
			if (min_t > a[j]){
				min_t = a[j];
				pos = j;
			}
		}
        //交换
		if (i != pos){
			int temp = a[i];
			a[i] = min_t;
			a[pos] = temp;
		}

	}
}

 时间复杂度：O(n^2)

空间复杂度：O(1)

稳定性：不稳定，由于交换，相同数据相对位置会发送改变。

        2.2.2 堆排序

        详情可以看博客堆排序与相关时间复杂度，里面我有详细介绍。

 时间复杂度：O(n*log(n))

空间复杂度：O(1)

稳定性：不稳定，由于交换，相同数据相对位置会发送改变。

        2.3 交换排序

        原理：根据序列中的两个键值的比较结果，交换两键值位置的值。交换的特点是：将较大值往后移动，将较小值往前移动。

        2.3.1 冒泡排序

        原理：通过相邻两元素比较，将待排序元素的最大值移动到最大下标处。

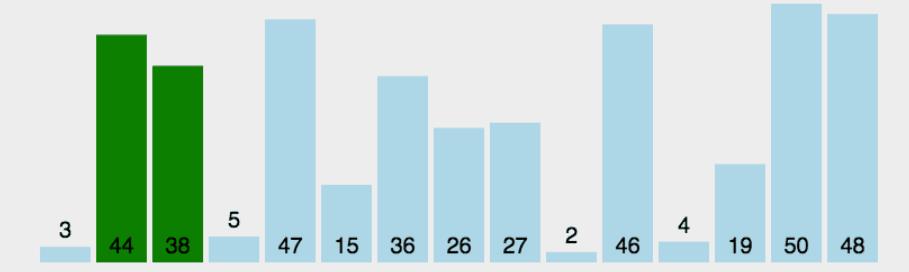 编码：

每次冒泡都会选出当前区间最大值或者最小值。

1. 比较相邻元素，将较大的值交换到后面，这样就将最大值移到最后了。
2. 注意控制区间范围。外层为区间元素个数，每次减少一个(为最后一个)。里层进行比较。

//将最大的数交换到最大下标处
void BubbleSort(int arr[], int n){
	//控制区间大小
	for (int i = n-1; i >=0 ; i--){
		int flag = 0;//记录是否进行交换
		for (int j = 0; j < i; j++){
			//相邻两元素比较
			if (arr[j]>arr[j + 1]){
				Swap(&arr[j], &arr[j + 1]);
				flag = 1;
			}

		}
		//没有进行交换，说明已经有序
		if (flag == 0){
			break;
		}
	}
}

时间复杂度：O(n^2)

空间复杂度：O(1)

稳定性：稳定，虽然也存在交换，但是相同的数并不存在交换所以稳定。

         2.3.2 快速排序

        快速排序我在快速排序(递归和非递归)及其优化博客有详细说明。

        2.4归并排序

        归并排序在博客归并排序算法有详细说明。

这里增加一个外排序：

首先，我先说明一下什么是内排序，什么是外排序：
 内排序：数据量相对少一些，可以放到内存中进行排序。
 外排序：数据量较大，内存中放不下，数据只能放到磁盘文件中，需要排序。

 上面介绍的排序算法均是在内存中进行的，对于数据量庞大的序列，上面介绍的排序算法都束手无策，而归并排序却能胜任这种海量数据的排序。

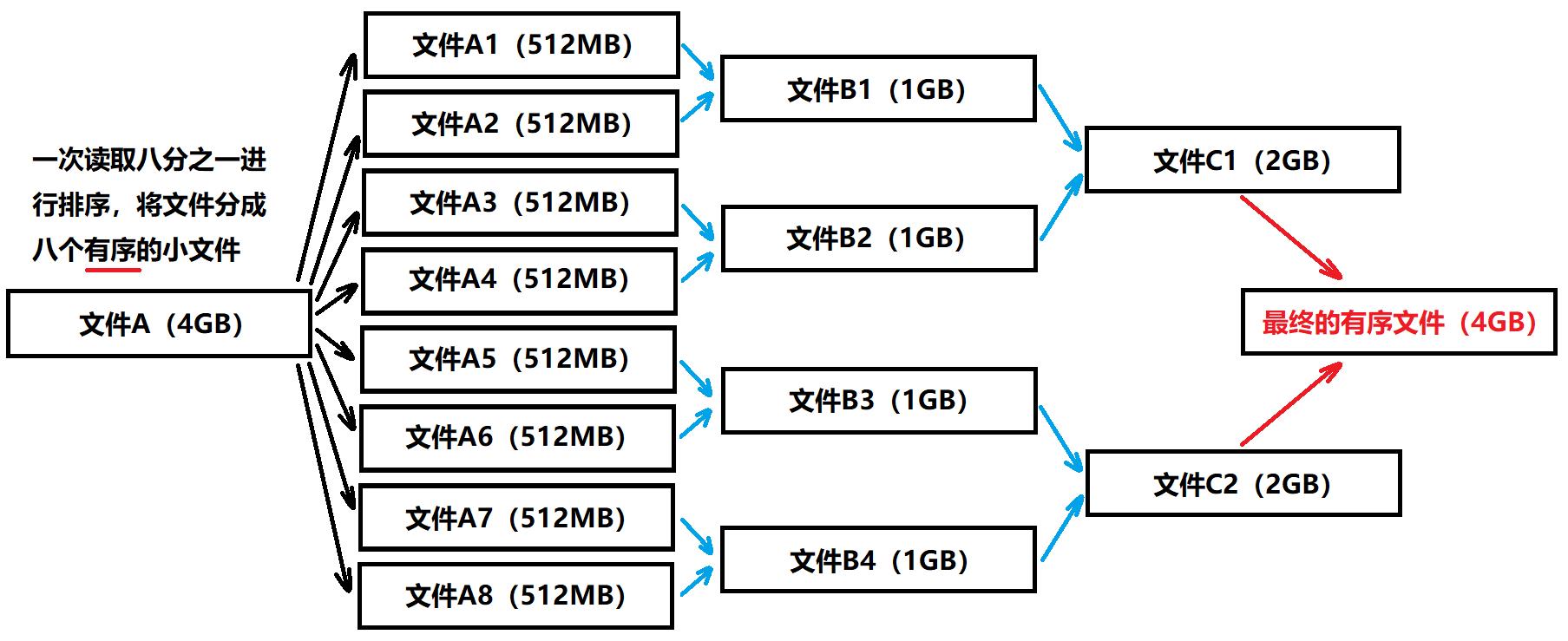
 假设现在有10亿个整数（4GB）存放在文件A中，需要我们进行排序，而内存一次只能提供512MB空间，归并排序解决该问题的基本思路如下：
 1、每次从文件A中读取八分之一，即512MB到内存中进行排序（内排序），并将排序结果写入到一个文件中，然后再读取八分之一，重复这个过程。那么最终会生成8个各自有序的小文件（A1~A8）。
 2、对生成的8个小文件进行11合并，最终8个文件被合成为4个，然后再11合并，就变成2个文件了，最后再进行一次11合并，就变成1个有序文件了。

注意：这里将两个文件进行11合并，并不是先将两个文件读入内存然后进行合并，因为内存装不下。这里的11合并是利用文件输入输出函数，从两个文件中各自读取一个数据，然后进行比较，将较小的数据写入到一个新文件中去，然后再读取，再比较，再写入，最终将两个文件中的数据全部写入到另一个文件中去，那么此时这个文件又是一个有序的文件了。

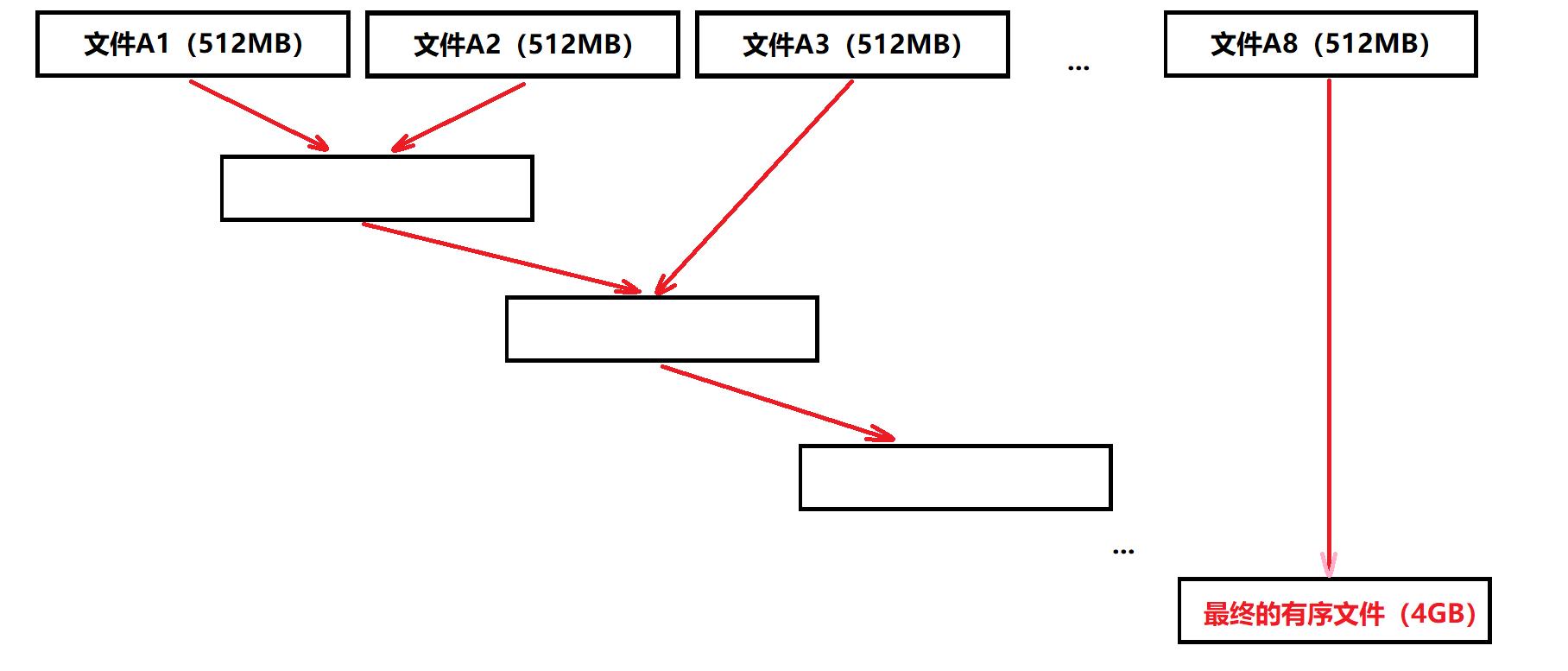
当然，你也可以这样合并文件：

  2.5 计数排序

        思想：开辟一个数组，来记录待排序元素中，元素的个数。根据统计的结果，从大到小(小到大)，在写到原来数组中。

        这里利用了哈希直接定址法的实现，将数映射到数组中，在按照数组，将数映射回原来的数组中。

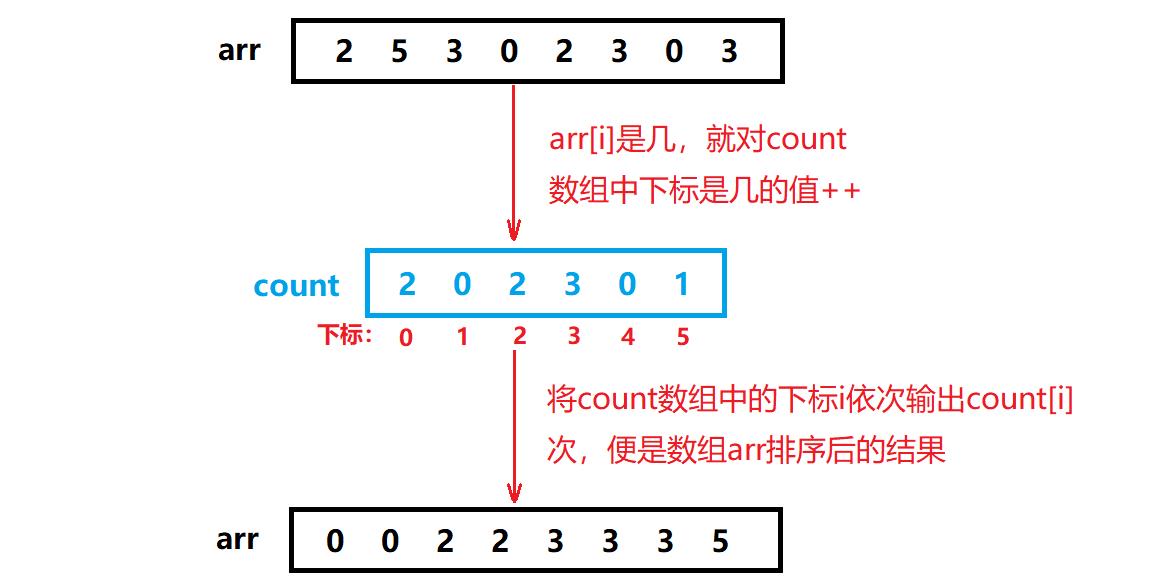
        映射方式有两种：

1. 绝对映射：元素的值直接映射到对应下标处。
2. 相对映射：按照y=ax+b的关系映射到下标y处。

计数排序算法在数据范围比较集中时，效率很高，并且只适用于整数。

//计数排序
void CountSort(int* a, int n)
{
	int min = a[0];//记录数组中的最小值
	int max = a[0];//记录数组中的最大值
	for (int i = 0; i < n; i++)
	{
		if (a[i] < min)
			min = a[i];
		if (a[i] > max)
			max = a[i];
	}
	int range = max - min + 1;//min和max之间的自然数个数（包括min和max本身）
	int* count = (int*)calloc(range, sizeof(int));//开辟可储存range个整型的内存空间，并将内存空间置0
	if (count == NULL)
	{
		printf("malloc fail\\n");
		exit(-1);
	}
	//统计相同元素出现次数（相对映射）
	for (int i = 0; i < n; i++)
	{
		count[a[i] - min]++;
	}
	int i = 0;
	//根据统计结果将序列回收到原来的序列中
	for (int j = 0; j < range; j++)
	{
		while (count[j]--)
		{
			a[i++] = j + min;
		}
	}
	free(count);//释放空间
}

有借鉴博客的图和外排序：https://blog.csdn.net/chenlong_cxy/article/details/116563972?ops_request_misc=%257B%2522request%255Fid%2522%253A%2522163358954616780357246597%2522%252C%2522scm%2522%253A%252220140713.130102334..%2522%257D&request_id=163358954616780357246597&biz_id=0&utm_medium=distribute.pc_search_result.none-task-blog-2~all~top_positive~default-1-116563972.pc_search_ecpm_flag&utm_term=%E6%8E%92%E5%BA%8F%E7%AE%97%E6%B3%95&spm=1018.2226.3001.4187