[Pytorch系列-27]:神经网络基础 - 多输入神经元实现波士顿房价预测
Posted 文火冰糖的硅基工坊
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了[Pytorch系列-27]:神经网络基础 - 多输入神经元实现波士顿房价预测相关的知识,希望对你有一定的参考价值。
作者主页(文火冰糖的硅基工坊):文火冰糖(王文兵)的博客_文火冰糖的硅基工坊_CSDN博客
本文网址:https://blog.csdn.net/HiWangWenBing/article/details/120605366
目录
前言 深度学习模型框架
第1章 业务领域分析
1.1 步骤1-1:业务领域分析

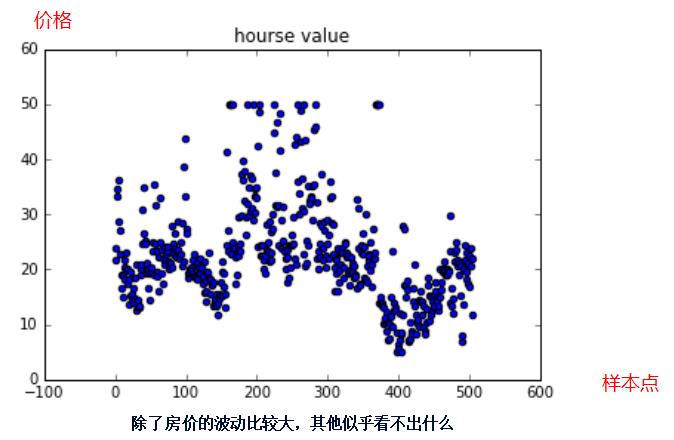
房价的起伏似乎没有规律,但决定房价的因素有12种,确实有规律可循的。
因此这个问题,实际上多元函数的非线性回归问题:
自变量:12个决定房价的维度。
因变量:最终的房价。
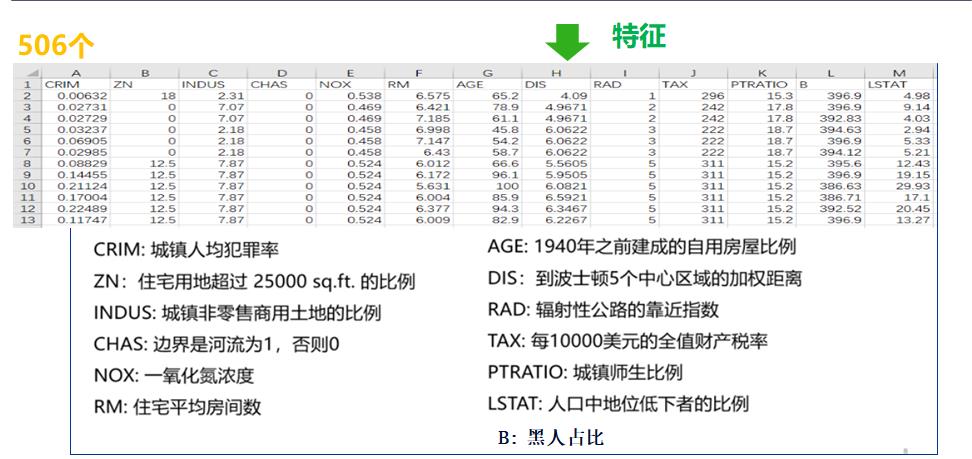
其中有13个影响因素。
1.2 步骤1-2:业务建模
单个神经元是都输入和单个输出。
可以构建两层的神经网络:

(1)隐藏层1:
- 输入属性数目:13
- 隐藏层神经元数目:30
- 隐藏层激活函数:relu
(2)输出层:
- 输入属性数目:30
- 隐藏层神经元数目:1
- 隐藏层激活函数:无
1.3 代码实例前置条件
#环境准备
import numpy as np # numpy数组库
import math # 数学运算库
import matplotlib.pyplot as plt # 画图库
import torch # torch基础库
import torch.nn as nn # torch神经网络库
import torch.nn.functional as F # torch神经网络库
from sklearn.datasets import load_boston
from sklearn.preprocessing import MinMaxScaler
from sklearn.model_selection import train_test_split
print("Hello World")
print(torch.__version__)
print(torch.cuda.is_available())Hello World 1.8.0 False
第2章 前向运算模型定义
2.1 步骤2-1:数据集选择
这里采用远程在线下载数据集:data_url = "http://lib.stat.cmu.edu/datasets/boston"
远程下载数据集的工具来源于:from sklearn.datasets import load_boston
#2-1 准备数据集
full_data = load_boston()
# 提前样本数据
x_raw_data = full_data['data']
print(x_raw_data.shape)
#提取样本标签
y_raw_data = full_data['target']
print(y_raw_data.shape)
y_raw_data = y_raw_data.reshape(-1,1)
print(y_raw_data.shape)
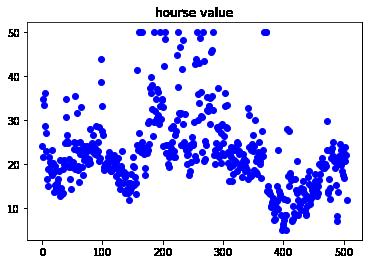
# 房价的波动范围
plt.scatter(range(len(y_raw_data)), y_raw_data, color="blue")
plt.title("hourse value")(506, 13) (506,) (506, 1)
2.2 步骤2-2:数据预处理
# 2-2 对数据预处理
print("数据规范化预处理,形状不变,内容改变")
ss = MinMaxScaler()
x_data = ss.fit_transform(x_raw_data)
y_data = y_raw_data
print(x_data.shape)
print(y_data.shape)
print("\\n把x、y从ndarray格式转成torch格式")
x_sample = torch.from_numpy(x_data).type(torch.FloatTensor)
y_sample = torch.from_numpy(y_data).type(torch.FloatTensor)
print(x_sample.shape)
print(y_sample.shape)
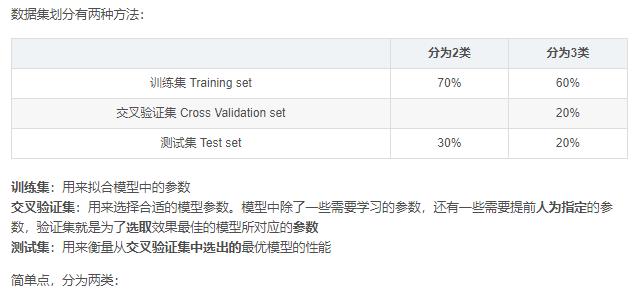
print("\\n数据集切割成:训练数据集和测试数据集")
# 0.2 表示测试集占比
x_train,x_test, y_train, y_test = train_test_split(x_sample , y_sample, test_size=0.2)
print(x_train.shape)
print(y_train.shape)
print(x_test.shape)
print(y_test.shape)数据规范化预处理,形状不变,内容改变 (506, 13) (506, 1) 把x、y从ndarray格式转成torch格式 torch.Size([506, 13]) torch.Size([506, 1]) 数据集切割成:训练数据集和测试数据集 torch.Size([404, 13]) torch.Size([404, 1]) torch.Size([102, 13]) torch.Size([102, 1])
2.3 步骤2-3:神经网络建模

# 2-3 定义网络模型
class Net(torch.nn.Module):
# 定义神经网络
def __init__(self, n_feature, n_hidden, n_output):
super(Net, self).__init__()
#定义隐藏层L1
# n_feature:输入属性的维度
# n_hidden: 神经元的个数 = 输出属性的个数
self.hidden = torch.nn.Linear(n_feature, n_hidden)
#定义输出层:
# n_hidden:输入属性的维度
# n_output: 神经元的个数 = 输出属性的个数
self.predict = torch.nn.Linear(n_hidden, n_output)
#定义前向运算
def forward(self, x):
h1 = self.hidden(x)
a1 = F.relu(h1)
out = self.predict(a1)
a2 = F.relu(out)
return a2
model = Net(13,30,1)
print(model)
print(model.parameters)
print(model.parameters())Net( (hidden): Linear(in_features=13, out_features=30, bias=True) (predict): Linear(in_features=30, out_features=1, bias=True) ) <bound method Module.parameters of Net( (hidden): Linear(in_features=13, out_features=30, bias=True) (predict): Linear(in_features=30, out_features=1, bias=True) )> <generator object Module.parameters at 0x000002922E120900>
2.4 步骤2-4:神经网络输出
# 2-4 定义网络预测输出
y_pred = model.forward(x_train)
print(y_pred.shape)torch.Size([404, 1])
第3章 后向运算模型定义
3.1 步骤3-1:定义loss函数
这里采用的MSE loss函数
# 3-1 定义loss函数:
# loss_fn= MSE loss
loss_fn = nn.MSELoss()
print(loss_fn)MSELoss()
3.2 步骤3-2:定义优化器
# 3-2 定义优化器
Learning_rate = 0.01 #学习率
# optimizer = SGD: 基本梯度下降法
# parameters:指明要优化的参数列表
# lr:指明学习率
optimizer = torch.optim.SGD(model.parameters(), lr = Learning_rate)
print(optimizer)SGD (
Parameter Group 0
dampening: 0
lr: 0.01
momentum: 0
nesterov: False
weight_decay: 0
)
3.3 步骤3-3:模型训练
# 3-3 模型训练
# 定义迭代次数
epochs = 100000
loss_history = [] #训练过程中的loss数据
y_pred_history =[] #中间的预测结果
for i in range(0, epochs):
#(1) 前向计算
y_pred = model(x_train)
#(2) 计算loss
loss = loss_fn(y_pred, y_train)
#(3) 反向求导
loss.backward()
#(4) 反向迭代
optimizer.step()
#(5) 复位优化器的梯度
optimizer.zero_grad()
# 记录训练数据
loss_history.append(loss.item())
y_pred_history.append(y_pred.data)
if(i % 10000 == 0):
print('epoch {} loss {:.4f}'.format(i, loss.item()))
print("\\n迭代完成")
print("final loss =", loss.item())
print(len(loss_history))
print(len(y_pred_history))epoch 0 loss 573.5384 epoch 10000 loss 5.3641 epoch 20000 loss 3.6727 epoch 30000 loss 3.0867 epoch 40000 loss 2.8373 epoch 50000 loss 2.2653 epoch 60000 loss 2.3308 epoch 70000 loss 2.1467 epoch 80000 loss 1.9769 epoch 90000 loss 1.7896 迭代完成 final loss = 1.9121897220611572 100000 100000
3.4 步骤3-4:模型验证
(1)训练集上验证
# 用训练集数据,检查训练效果
y_train_pred = model.forward(x_train)
loss_train = torch.mean((y_train_pred - y_train)**2)
print("loss for train:", loss_train.data)
plt.scatter(range(len(y_train)), y_train.data, color="blue")
plt.scatter(range(len(y_train_pred)), y_train_pred.data, color="red")
plt.title("hourse value")loss for train: tensor(1.8895)

训练集上的验证结果:
- 平均损失为:1.8895
- 预测点与实际的样本点接近度高。
(2)测试集上验证
# 用测试集数据,验证测试效果
y_test_pred = model.forward(x_test)
loss_test = torch.mean((y_test_pred - y_test)**2)
print("loss for test:", loss_test.data)
plt.scatter(range(len(y_test)), y_test.data, color="blue")
plt.scatter(range(len(y_test_pred)), y_test_pred.data, color="red")
plt.title("hourse value")loss for test: tensor(38.7100)
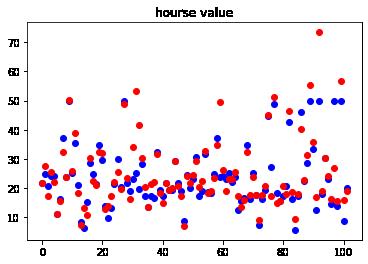
训练集上的验证结果:
- 平均损失为:38.7100,与 训练集相乘较大
- 预测点与实际的样本点偏差较大
- 模型在训练集上的损失远远好于测试集上的损失,模型的泛化能力较差。
3.5 步骤3-5:模型可视化
(1)前向数据
(2)后向loss值迭代过程
显示所有loss数据:
#显示loss的历史数据
plt.plot(loss_history, "r+")
plt.title("loss value")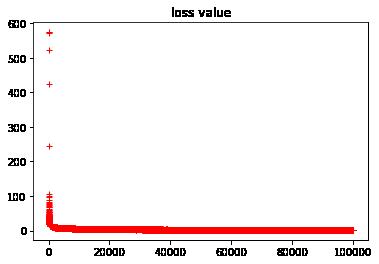
忽略掉前期快速收敛的数据,显示loss的局部收敛性
#显示loss的历史数据
plt.plot(loss_history[1000::], "r+")
plt.title("loss value") 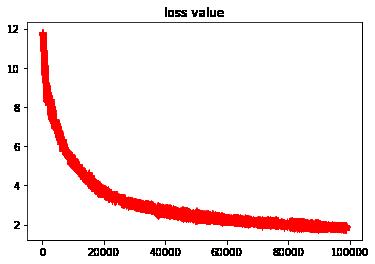
(3)前向预测函数的迭代过程
第4章 模型部署
4.1 步骤4-1:模型存储
#存储模型
torch.save(model, "models/boston_net.pkl")
4.2 步骤4-2:参数存储
#存储
torch.save(model.state_dict() , "models/boston_params.pkl")4.3 步骤4-3:模型还原
4.4 步骤4-3:参数还原
作者主页(文火冰糖的硅基工坊):文火冰糖(王文兵)的博客_文火冰糖的硅基工坊_CSDN博客
本文网址:https://blog.csdn.net/HiWangWenBing/article/details/120605366
以上是关于[Pytorch系列-27]:神经网络基础 - 多输入神经元实现波士顿房价预测的主要内容,如果未能解决你的问题,请参考以下文章
[Pytorch系列-25]:神经网络基础 - 单个无激活函数的神经元实现简单线性回归 - 2
[Pytorch系列-24]:神经网络基础 - 单个无激活函数的神经元实现简单线性回归 - 1
[Pytorch系列-26]:神经网络基础 - 多个带激活函数的神经元实现非线性回归
[Pytorch系列-28]:神经网络基础 - torch.nn模块功能列表
[Pytorch系列-50]:卷积神经网络 - FineTuning的统一处理流程与软件架构 - Pytorch代码实现
 https://blog.csdn.net/HiWangWenBing/article/details/120462734
https://blog.csdn.net/HiWangWenBing/article/details/120462734