[Pytorch系列-24]:神经网络基础 - 单个无激活函数的神经元实现简单线性回归 - 1
Posted 文火冰糖的硅基工坊
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了[Pytorch系列-24]:神经网络基础 - 单个无激活函数的神经元实现简单线性回归 - 1相关的知识,希望对你有一定的参考价值。
作者主页(文火冰糖的硅基工坊):文火冰糖(王文兵)的博客_文火冰糖的硅基工坊_CSDN博客
本文网址:https://blog.csdn.net/HiWangWenBing/article/details/120597547
目录
前言 深度学习模型框架
第1章 业务领域分析
1.1 步骤1-1:业务领域分析
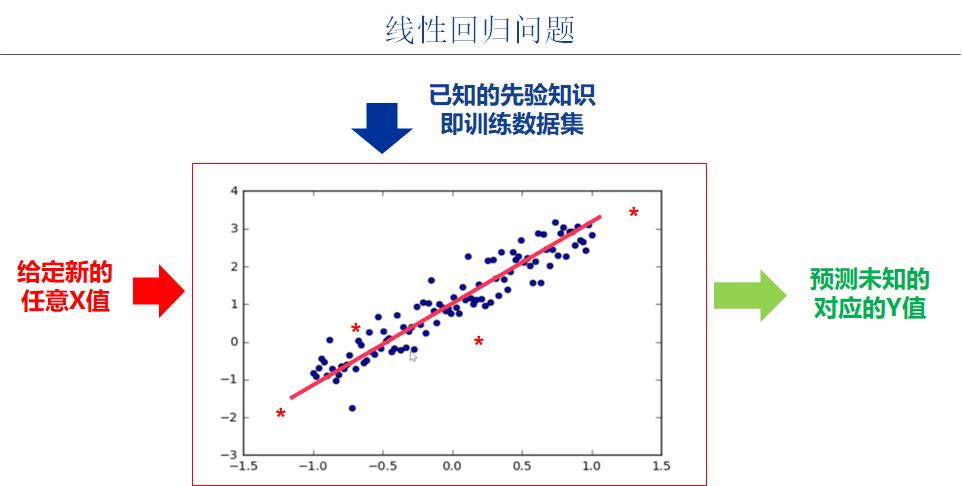
1.2 步骤1-2:业务建模
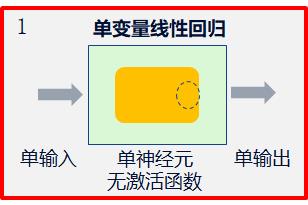
1.3 代码实例前置条件
#环境准备
import numpy as np # numpy数组库
import math # 数学运算库
import matplotlib.pyplot as plt # 画图库
import torch # torch基础库
import torch.nn as nn # torch神经网络库
print("Hello World")
print(torch.__version__)
print(torch.cuda.is_available())Hello World 1.8.0 False
第2章 前向运算模型定义
2.1 步骤2-1:数据集选择
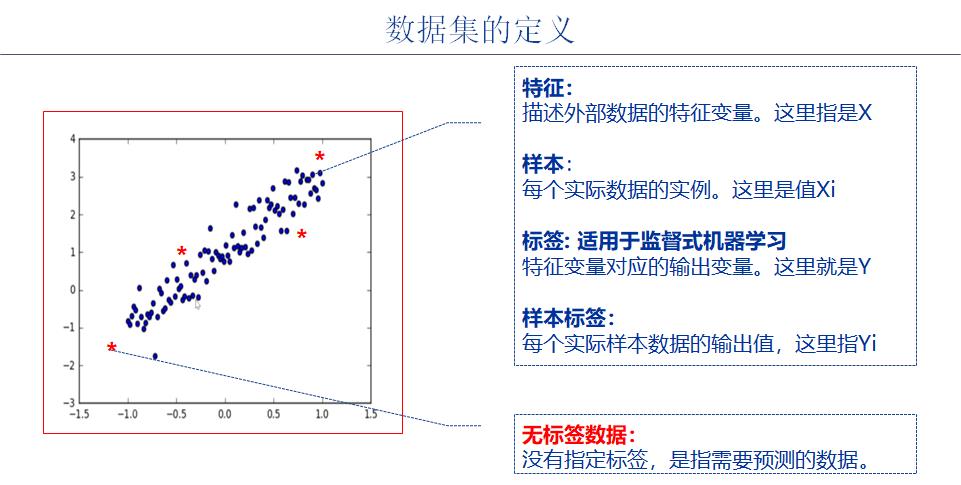
这里不需要采用已有的开源数据集,只需要自己构建数据集即可。
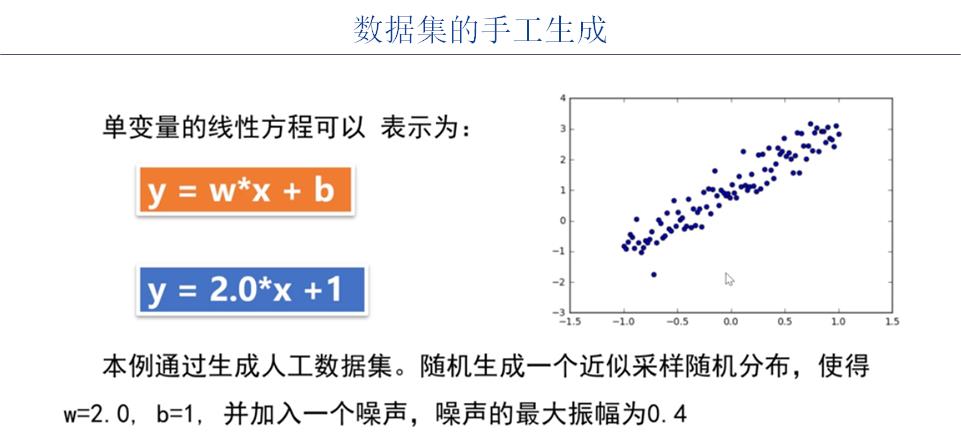
#2-1 准备数据集
x_sample = np.linspace(0, 5, 64)
noise = np.random.randn(64)
y_sample = 2 * x_sample + 1 + noise
y_line = 2 * x_sample + 1
#可视化数据
plt.scatter(x_sample, y_sample)
plt.plot(x_sample, y_line,'red')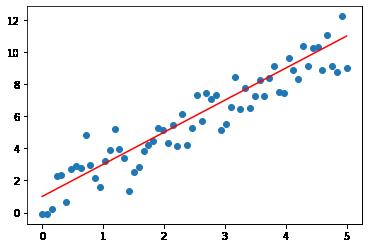
2.2 步骤2-2:数据预处理
(1)把numpy一维数据转换成二维样本数据
(2)把numpy样本数据转换成torch样本数据
# 2-2 对数据预处理
print("Numpy原始样本的形状")
print(x_sample.shape)
print(y_sample.shape)
# 把一维线性数据转换成二维样本数据,每个样本数据为一维
print("\\nNumpy训练样本的形状")
x_numpy = x_sample.reshape(-1, 1).astype('float32')
y_numpy = y_sample.reshape(-1, 1).astype('float32')
print(x_numpy.shape)
print(y_numpy.shape)
# numpy样本数据转换成pytorch样本数据
print("\\ntorch训练样本的形状")
x_train = torch.from_numpy(x_numpy)
y_train = torch.from_numpy(y_numpy)
print(x_train.shape)
print(y_train.shape)
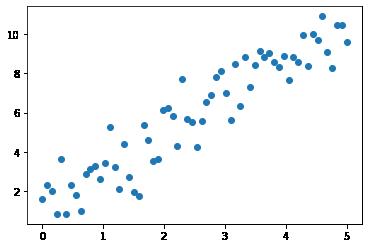
plt.scatter(x_train, y_train)Numpy原始样本的形状 (64,) (64,) Numpy训练样本的形状 (64, 1) (64, 1) torch训练样本的形状 torch.Size([64, 1]) torch.Size([64, 1])
Out[3]:
<matplotlib.collections.PathCollection at 0x1fdc56524f0>
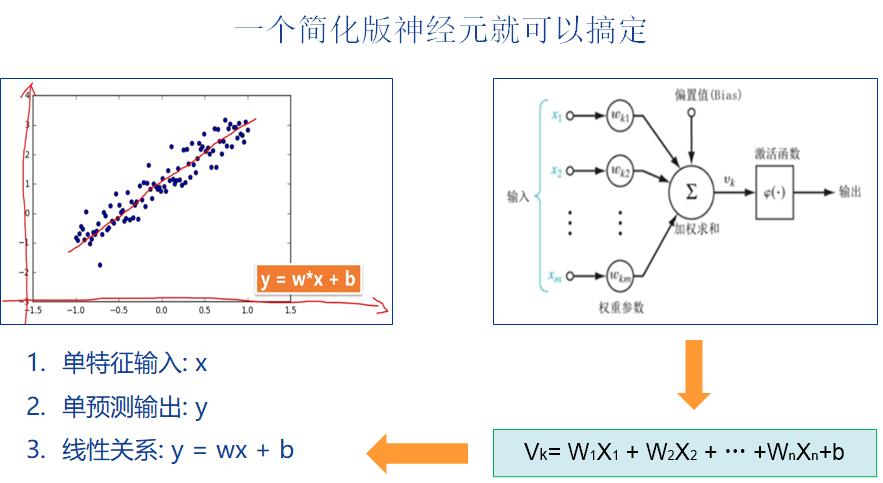
2.3 步骤2-3:神经网络建模
这里的神经网络模型是单输入(size=1)、单输出(size=1)、无激活函数的线性神经元。
# 2-3 定义网络模型
# in_features: 输入数据的size = 1
# out_features: 输处数据的size = 1
# bias = True: 打开偏置参数B
print("定义并初始化模型")
model = nn.Linear(in_features=1, out_features=1)
print(model)
print("\\n获取W,B参数的初始化值(随机产生)")
w,b = model.parameters()
print(w)
print(b)定义并初始化模型 Linear(in_features=1, out_features=1, bias=True) 获取W,B参数的初始化值(随机产生) Parameter containing: tensor([[-0.3860]], requires_grad=True) Parameter containing: tensor([-0.7404], requires_grad=True)
备注:
神经网络中w,b参数的初始值是随机初始,每次调用nn.Linear创建神经网络,W, B参数都不一样。
2.4 步骤2-4:神经网络输出
# 2-4 定义网络预测输出
y_pred = model.forward(x_train)
print(y_pred.shape)torch.Size([64, 1])
备注:输出是64个样本的一维数据
第3章 后向运算模型定义
3.1 步骤3-1:定义loss函数
这里采用的MSE loss函数
# 3-1 定义loss函数:
# loss_fn= MSE loss
loss_fn = nn.MSELoss()
print(loss_fn)MSELoss()
3.2 步骤3-2:定义优化器
# 3-2 定义优化器
Learning_rate = 0.01 #学习率
# optimizer = SGD: 基本梯度下降法
# parameters:指明要优化的参数列表
# lr:指明学习率
optimizer = torch.optim.SGD(model.parameters(), lr = Learning_rate)
print(optimizer)SGD (
Parameter Group 0
dampening: 0
lr: 0.01
momentum: 0
nesterov: False
weight_decay: 0
)
备注:优化器需要指明优化的参数列表和学习率
3.3 步骤3-3:模型训练
# 3-3 模型训练
# 定义迭代次数
epochs = 500
loss_history = [] #训练过程中的loss数据
w_history = [] #训练过程中的w参数值
b_history = [] #训练过程中的b参数值
for i in range(0, epochs):
#(1) 前向计算
y_pred = model(x_train)
#(2) 计算loss
loss = loss_fn(y_pred, y_train)
#(3) 反向求导
loss.backward()
#(4) 反向迭代
optimizer.step()
#(5) 复位优化器的梯度
optimizer.zero_grad()
w, b = model.parameters()
loss_history.append(loss.item())
w_history.append(w.item())
b_history.append(b.item())
if(i % 100 == 0):
print('epoch {} loss {:.4f}'.format(i, loss.item()))
print("\\n迭代完成")
w, b = model.parameters() #parameters()返回的是一个迭代器指向的对象
print("\\n训练后w参数值:", w, w.item())
print("\\n训练后b参数值:", b, b.item())
print("\\n最小损失数值 :", loss, loss.item())
print(len(loss_history))
print(len(w_history))
print(len(b_history))epoch 0 loss 42.0689 epoch 100 loss 1.0441 epoch 200 loss 1.0440 epoch 300 loss 1.0439 epoch 400 loss 1.0439 迭代完成 训练后w参数值: Parameter containing: tensor([[1.8530]], requires_grad=True) 1.8529784679412842 训练后b参数值: Parameter containing: tensor([1.2702], requires_grad=True) 1.2701895236968994 最小损失数值 : tensor(1.0439, grad_fn=<MseLossBackward>) 1.0438624620437622 500 500 500
3.4 步骤3-4:模型验证
NA
3.5 步骤3-5:模型可视化
# 3-4 可视化模型数据
#model返回的是总tensor,包含grad_fn,用data提取出的tensor是纯tensor
y_pred = model.forward(x_train).data.numpy().squeeze()
print(x_train.shape)
print(y_pred.shape)
print(y_line.shape)
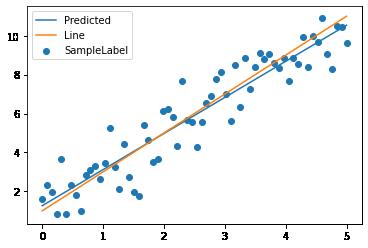
plt.scatter(x_train, y_train, label='SampleLabel')
plt.plot(x_train, y_pred, label='Predicted')
plt.plot(x_train, y_line, label='Line')
plt.legend()
plt.show()torch.Size([64, 1]) (64,) (64,)
#显示loss的历史数据
plt.plot(loss_history, "r+")
plt.title("loss value")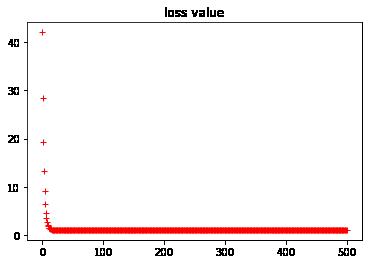
#显示w参数的历史数据
plt.plot(w_history, "r+")
plt.title("w value")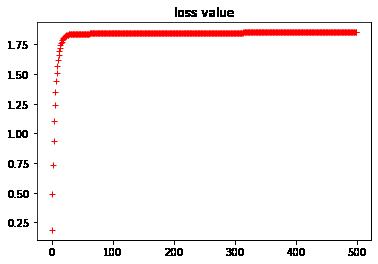
#显示b参数的历史数据
plt.plot(b_history, "r+")
plt.title("b value")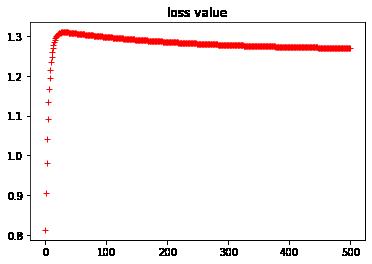
第4章 模型部署
4.1 步骤4-1:模型部署
NA
作者主页(文火冰糖的硅基工坊):文火冰糖(王文兵)的博客_文火冰糖的硅基工坊_CSDN博客
本文网址:https://blog.csdn.net/HiWangWenBing/article/details/120597547
以上是关于[Pytorch系列-24]:神经网络基础 - 单个无激活函数的神经元实现简单线性回归 - 1的主要内容,如果未能解决你的问题,请参考以下文章
[Pytorch系列-27]:神经网络基础 - 多输入神经元实现波士顿房价预测
[Pytorch系列-25]:神经网络基础 - 单个无激活函数的神经元实现简单线性回归 - 2
[Pytorch系列-26]:神经网络基础 - 多个带激活函数的神经元实现非线性回归
[Pytorch系列-28]:神经网络基础 - torch.nn模块功能列表
[Pytorch系列-50]:卷积神经网络 - FineTuning的统一处理流程与软件架构 - Pytorch代码实现
 https://blog.csdn.net/HiWangWenBing/article/details/120462734
https://blog.csdn.net/HiWangWenBing/article/details/120462734