数据结构内部排序算法汇总

Posted 2021-10-17 看淡所有的不辞而别

一.简单选择排序（比较类排序）

1.基本思想：每一趟找到该次最小值的位置，然后和当前元素交换。
2.时间复杂度：两次for循环
(1)最好情况O(n^2)
(2)平均情况O(n^2)
(3)最坏情况O(n^2)
3.空间复杂度为O(1)；没有用到额外的空间
4.排序稳定性：不稳定

在一趟选择，如果一个元素比当前元素小，而该小的元素又出现在一个和当前元素相等的元素后面，那么交换后稳定性就被破坏了。所以选择排序是一个不稳定的排序算法。

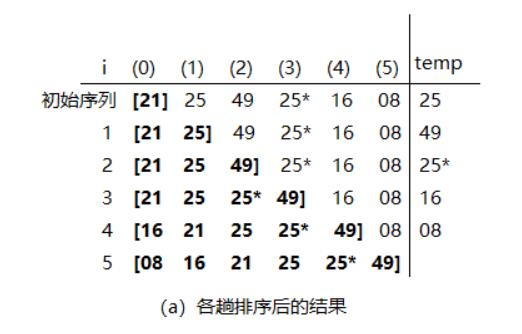
如图可以看出相对次序已经改变

5.代码

void select_sort() //简单选择排序(按位置每次循环选择最小的)
{
    for (int i = 0; i < n - 1; i++)
    {
        int k = i; //初始化最小值的下标
        for (int j = i + 1; j < n; j++)
        {
            if (q[k] > q[j])
            {
                k = j;
            }
        }
        swap(q[i], q[k]); //将最小值放到合适的位置
    }
}

二、插入排序（比较类排序）

a.直接插入排序

1.基本思想： 每一步将一个待排序的元素，按其排序码的大小，插入到前面已经排好序的一组元素的适当位置。

具体：当插入第i(i >=> 1)时，前面的V[0]，V[1]，……，V[i-1]已经排好序。这时，用V[I]的排序码与V[i-1]，V[i-2]，…的排序码顺序进行比较，找到插入位置即将V[i]插入，原来位置上的元素向后顺移。

2.时间复杂度
(1)最好情况O(n)；全都是顺序，只用一重循环
(2)平均情况O(n^2)
(3)最坏情况O(n^2)
3.空间复杂度：O(1)
4.排序稳定性：稳定
5.代码

void insert_sort() //直接插入排序
{
    for (int i = 1; i < n; i++)
    {
        int t = q[i], j = i;
        while (j && q[j - 1] > t)
        {
            q[j] = q[j - 1];
            j--;
        }
        q[j] = t;
    }
} 

b.折半插入排序

1.方法：在查找时利用二分法找到第一个大于插入元素的位置，其他都与直接插入排序相同
2.代码

void binary_search_insert_sort() //二分插入排序
{
    for (int i = 1; i < n; i++)
    {
        if (q[i - 1] < q[i])
            continue; //特判一下全部小于插入元素的情况
        int t = q[i];
        int l = 0, r = i - 1;
        while (l < r) //找到第一个大于插入元素的位置
        {
            int mid = l + r >> 1;
            if (q[mid] > t)
                r = mid;
            else
                l = mid + 1;
        }
        for (int j = i - 1; j >= r; j--)
            q[j + 1] = q[j]; //大于插入元素的位置全部向后移动一位
        q[r] = t;
    }
}

三、冒泡排序（比较类排序）

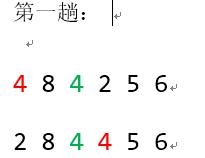
1.基本思想：每一次把一个元素放到未排序序列最小的位置(分为两个序列，左边是已经排好序的，右边是未排序的)，但要注意是从后往前比较的。
2.时间复杂度
(1)最好情况O(n)；全都是顺序，一次比较后，直接结束
(2)平均情况O(n^2)
(3)最坏情况O(n^2)
3.空间复杂度：O(1)
4.排序稳定性：稳定
5.代码

void bubble_sort()
{
    for (int i = 0; i < n - 1; i++)
    {
        bool has_swap = false;
        for (int j = n - 1; j > i; j--) //前i个已经排好序
        {
            if (q[j] < q[j - 1])
            {
                swap(q[j], q[j - 1]);
                has_swap = true;
            }
        }
        if (!has_swap)
            break;
    }
}

结语

第一篇文章写了比较简单的三个排序算法，时间复杂度的平均情况都在O(n^2)，效率不高，下一篇文章将讲解希尔排序、堆排序、快速排序等相对比较快的排序算法。
本文借鉴了许多博客的思想，代码都是y总的模板，非常简洁明了。文章只做日后的温习使用。
个人博客地址