八大排序算图解汇总

Posted 2022-01-26 爱学习的大鱼

1.排序的介绍

排序也成为排序算法(Sort Algoritm)，排序是将一组数据,按指定的顺序进行排列的过程。

2. 排序的分类

• 内部排序法：

  将需要处理的所有数据都加载到内部存储器(内存)中进行排序

• 外部排序法

  数据量过大，无法全部加载到内存中，需要借助外部存储(如文件)进行排序。

• 常见的排序算法分类如下图：

  

  相关术语解释：

  1)稳定：如果a原本在b前面，而a=b，排序之后a仍然在b的前面；

  2)不稳定：如果a原本在b的前面，而a=b，排序之后a可能会出现在b的后面；

  3)内排序：所有排序操作都在内存中完成；

  4)外排序：由于数据太大，因此把数据放在磁盘中，而排序通过磁盘和内存的数据传输才能进行；

  5)时间复杂度： 一个算法执行所耗费的时间。

  6)空间复杂度：运行完一个程序所需内存的大小。

  7)n: 数据规模

3.排序算法的时间和空间复杂度

排序方法	时间复杂度(平均)	时间复杂度(最坏)	时间复杂度(最好)	空间复杂度	稳定性	复杂性
直接插入排序	O(n2)	O(n2)	O(n)	O(1)	稳定	简单
希尔排序	O(nlog2n)	O(n2)	O(n1.3)	O(1)	不稳定	较复杂
直接选择排序	O(n2)	O(n2)	O(n2)	O(1)	不稳定	简单
堆排序	O(nlog2n)	O(nlog2n)	O(nlog2n)	O(1)	不稳定	较复杂
冒泡排序	O(n2)	O(n2)	O(n)	O(1)	稳定	简单
快速排序	O(nlog2n)	O(n2)	O(nlog2n)	O(nlog2n)	不稳定	较复杂
归并排序	O(nlog2n)	O(nlog2n)	O(nlog2n)	O(n)	稳定	较复杂
基数排序	O(d(n+r))	O(d(n+r))	O(d(n+r))	O(n+r)	稳定	较复杂

4. 排序算法原理即代码实现

4.1 冒泡排序

4.1.1 介绍

冒泡排序（Bubble Sort） 最为简单的一种排序，通过重复走完数组的所有元素，通过打擂台的方式两两比较，直到没有数可以交换的时候结束这个数，再到下个数，直到整个数组排好顺序。因一个个浮出所以叫冒泡排序。双重循环时间 复杂度O(n^2)

4.1.2 算法步骤

• 比较相邻两个数据如果。第一个比第二个大，就交换两个数
• 对每一个相邻的数做同样1的工作，这样从开始一队到结尾一队在最后的数就是最大的数。
• 针对所有元素上面的操作，除了最后一个。
• 重复1~3步骤，直到顺序完成。

4.1.3 动画演示

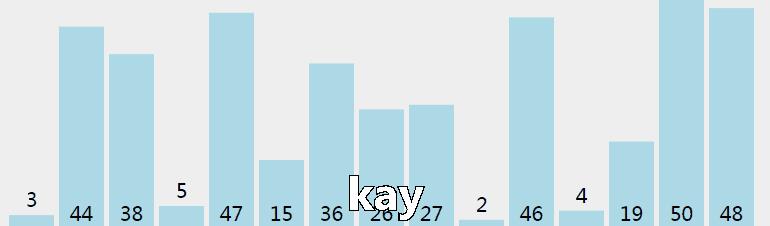
4.1.4 java 代码实现和数据测试

/**
 * @author 谢阳
 * @version 1.8.0_131
 */
public class BubbleSort 
    public static void main(String[] args) 
        //时间复杂度为O(n^2)
        int[] arr = new int[80000];
        for (int i = 0; i < 80000; i++) 
            arr[i] = (int)(Math.random()*1000000);
        
        long time = System.currentTimeMillis();
        //sort1(arr);//未优化 time = 14536 time = 14184 time = 13270
        sort2(arr);//优化 time = 13075  time = 13539 time = 13388
        System.out.println("time = " + (System.currentTimeMillis() - time));

    

    //冒泡排序
    public static void sort1(int[] arr) 
        //数组长度
        int len = arr.length;
        for (int i = 0; i < len - 1; i++) 
            for (int j = 0; j < len - i - 1; j++) 
                //前一个元素大于后一个元素则交换
                if (arr[j] > arr[j + 1]) 
                    int temp = arr[j];
                    arr[j] = arr[j + 1];
                    arr[j + 1] = temp;
                
            
        
    

    //冒泡排序优化
    public static void sort2(int[] arr) 
        int len = arr.length;
        //标志位
        boolean flag;
        for (int i = 0; i < len - 1; i++) 
            //未交换 为true
            flag = true;
            for (int j = 0; j < len - i - 1; j++) 
                //前一个元素大于后一个元素则交换
                if (arr[j] > arr[j + 1]) 
                    //有交换则为false
                    flag = false;
                    int temp = arr[j];
                    arr[j] = arr[j + 1];
                    arr[j + 1] = temp;
                
            
            //System.out.printf("第%d次交换:%s\\n", i + 1, Arrays.toString(arr));
            //标志未变化则有序无需在进行交换
            if (flag) 
                break;
            
        
    

4.2 选择排序

4.2.1 介绍

选择排序（Select Sort） 是直观的排序，通过确定一个 Key 最大或最小值，再从带排序的的数中找出最大或最小的交换到对应位置。再选择次之。双重循环时间复杂度为 O(n^2)

4.2.2 算法步骤

• 首先在未排序序列中找到最小（大）元素，存放到排序序列的起始位置。
• 再从剩余未排序元素中继续寻找最小（大）元素，然后放到已排序序列的末尾。
• 重复第二步，直到所有元素均排序完毕。

4.2.3 动画演示

4.2.4 java 代码实现和数据测试

import java.util.Arrays;

/**
 * @author 谢阳
 * @version 1.8.0_131
 */
public class SelectSort 
    public static void main(String[] args) 

        //时间复杂度为O(n^2)
        int[] arr = new int[80000];
        for (int i = 0; i < 80000; i++) 
            arr[i] = (int)(Math.random()*1000000);
        
        long time = System.currentTimeMillis();
        sort(arr);
        //time = 5168  time = 5228  time = 5172
        //时间比冒泡快,因为减少了交换数据的次数
        System.out.println("time = " + (System.currentTimeMillis() - time));
        //int[] arr = -1,-42,213,3,1,-423,23,12,0;
        //sort(arr);
        //System.out.println(Arrays.toString(arr));
    

    //选择排序
    public static void sort(int[] arr) 
        //定义最小数
        int min;
        //定义标识符
        int index;
        //数组长度
        int len = arr.length;
        for (int i = 0; i < len - 1; i++) 
            min = arr[i];
            index = i;
            for (int j = i + 1; j < len; j++) 
                if (min < arr[j]) 
                    min = arr[j];
                    index = j;
                
            
            if (index != i) 
                arr[index] = arr[i];
                arr[i] = min;
            
            //System.out.printf("第%d次交换:%s\\n", i + 1, Arrays.toString(arr));
        
    

4.3 插入排序

4.3.1 介绍

插入排序(InsertionSort)，一般也被称为直接插入排序。对于少量元素的排序，它是一个有效的算法。双重循环时间复杂度为 O(n^2)

4.3.2 算法步骤

• 将第一待排序序列第一个元素看做一个有序序列，把第二个元素到最后一个元素当成是未排序序列。
• 从头到尾依次扫描未排序序列，将扫描到的每个元素插入有序序列的适当位置。（如果待插入的元素与有序序列中的某个元素相等，则将待插入元素插入到相等元素的后面。）

4.3.3 动画演示

4.3.4 java 代码实现和数据测试

/**
 * @author 谢阳
 * @version 1.8.0_131
 */
public class InsertSort 
    public static void main(String[] args) 
        //时间复杂度为O(n^2)
        int[] arr = new int[80000];
        for (int i = 0; i < 80000; i++) 
            arr[i] = (int) (Math.random() * 1000000);
        
        long time = System.currentTimeMillis();
        sort(arr);
        //time = 852 time = 826 time = 836 time = 776
        System.out.println("time = " + (System.currentTimeMillis() - time));
        //int[] arr = new int[]6, 5, 4, 3, 2, 1;
        //sort(arr);
        //System.out.println(Arrays.toString(arr));
    

    //插入排序
    public static void sort(int[] arr) 
        int len = arr.length;

        int insert;
        int index;

        for (int i = 1; i < len; i++) 
            insert = arr[i];
            index = i - 1;
            while (index >= 0 && arr[index] > insert) 
                arr[index + 1] = arr[index];
                index--;
            
            arr[index + 1] = insert;
            //System.out.printf("第%d次交换:%s\\n", i + 1, Arrays.toString(arr));
        

    

4.4 希尔排序

4.4.1 介绍

希尔排序是希尔（Donald Shell）于1959年提出的一种排序算法。希尔排序也是一种插入排序，它是简单插入排序经过改进之后的一个更高效的版本，也称为缩小增量排序。

4.4.2 算法步骤

• 选择一个增量序列 t1，t2，……，tk，其中 ti > tj, tk = 1；
• 按增量序列个数 k，对序列进行 k 趟排序；
• 每趟排序，根据对应的增量 ti，将待排序列分割成若干长度为 m 的子序列，分别对各子表进行直接插入排序。仅增量因子为 1 时，整个序列作为一个表来处理，表长度即为整个序列的长度。

4.4.3 动画演示

4.4.4 java 代码实现和数据测试

import java.util.Arrays;

/**
 * @author 谢阳
 * @version 1.8.0_131
 */
public class ShellSort 
    public static void main(String[] args) 
        //时间复杂度为O(log2n)

        int[] arr = new int[80000];
        for (int i = 0; i < 80000; i++) 
            arr[i] = (int) (Math.random() * 1000000);
        
        long time = System.currentTimeMillis();
        sort2(arr);
        //time = 23 time = 20 time = 21
        System.out.println("time = " + (System.currentTimeMillis() - time));

        //int[] arr = 8, 9, 1, 7, 2, 3, 5, 4, 6, 0;
        //sort2(arr);
    

    //希尔排序(交换法效率低) time = 8053  略快于冒泡排序
    public static void sort1(int[] arr) 
        int len = arr.length;
        int temp;
        for (int gap = len / 2; gap > 0; gap /= 2) 
            for (int i = gap; i < len; i++) 
                for (int j = i - gap; j >= 0; j -= gap) 
                    if (arr[j] > arr[j + gap]) 
                        temp = arr[j];
                        arr[j] = arr[j + gap];
                        arr[j + gap] = temp;
                    
                
            
            System.out.println(Arrays.toString(arr));
        
    

    //希尔排序(插入法) time = 21
    public static void sort2(int[] arr) 
        //插入值
        int insert;
        //标识符,插入值的上一个分组内的值坐标
        int index;
        int len = arr.length;
        for (int gap = len / 2; gap > 0; gap /= 2) //分组,每次除2
            for (int i = gap; i < len; i++)  //对分组排序
                insert = arr[i];
                index = i - gap;
                //分组内部插入排序 上个坐标大于等于0 且上个坐标值大于插入值
                if (arr[index] > insert) //优化数据量越大效果越明显
                    while (index >= 0 && arr[index] > insert) 
                        //满足交换 坐标后移
                        arr[index + gap] = arr[index];
                        index -= gap;
                    
                    //交换完成后给对应坐标赋值
                    arr[index + gap] = insert;
                
            
            //System.out.println(Arrays.toString(arr));

        
    

4.5 快速排序

4.5.1 介绍

快速排序是由东尼·霍尔所发展的一种排序算法。在平均状况下，排序 n 个项目要 Ο(nlogn) 次比较。在最坏状况下则需要 Ο(n2) 次比较，但这种状况并不常见。事实上，快速排序通常明显比其他 Ο(nlogn) 算法更快，因为它的内部循环（inner loop）可以在大部分的架构上很有效率地被实现出来。

4.5.2 算法步骤

• 从数列中挑出一个元素，称为 "基准"（pivot）;
• 重新排序数列，所有元素比基准值小的摆放在基准前面，所有元素比基准值大的摆在基准的后面（相同的数可以到任一边）。在这个分区退出之后，该基准就处于数列的中间位置。这个称为分区（partition）操作；
• 递归地（recursive）把小于基准值元素的子数列和大于基准值元素的子数列排序；

4.5.3 动画演示

4.5.4 java 代码实现和数据测试

import java.util.Arrays;

/**
 * @author 谢阳
 * @version 1.8.0_131
 */
public class QuickSort 
    public static void main(String[] args) 
        int[] arr = new int[80000];
        for (int i = 0; i < 80000; i++) 
            arr[i] = (int) (Math.random() * 1000000);
        
        long time = System.currentTimeMillis();
        sort1(arr, 0, arr.length - 1);//time = 20 time = 10 time = 30
        //sort2(arr, 0, arr.length - 1);//time = 30 time = 20time = 32
        System.out.println("time = " + (System.currentTimeMillis() - time));

        //int[] arr = 9, 8, 7, 6, 5, 4, 3, 2, 1;
        //System.out.println(arr.length - 1);
        //sort1(arr, 0, arr.length - 1);
        //System.out.println(Arrays.toString(arr));
    

    //取左值
    private static void sort1(int[] arr, int left, int right) 
        if (left < right) 
            //设置基准值的位置
            int pivot = left;
            //比较开始值
            int index = pivot + 1;
            //循环将比pivot小的值放在index-1(后面新的pivot)的左边,大的值放右边
            for (int i = index; i <= right; i++) 
                if (arr[i] < arr[pivot]) 
                    swap(arr, i, index);
                    index++;
                
            
            //交换index的值
            swap(arr, pivot, index - 1);

            //定义新的基础下标
            pivot = index - 1;
            //左遍历,基准下标左移
            sort1(arr, left, pivot - 1);
            //右遍历,基准下标右移
            sort1(arr, pivot + 1, right);
        
    

    //取中间值
    public static void sort2(int[] arr, int left, int right) 
        int r = right;                  //右标志位
        int l = left;                   //坐标值位
        int pivot = arr[(r + l) / 2];   //中间值(基准值)

        //循环条件
        while (l < r) 
            //左值小于中间值,则向右移动一位,直到找到大于中间值或中间值为止,得到该值坐标l
            while (arr[l] < pivot) 
                l++;
            

            //中间值小于右值,则向左移动一位,直到找到小于中间值或中间值为止,得到该值坐标r
            while (pivot < arr[r]) 
                r--;
            

            //如果r>=l则退出循环
            if (l >= r) 
                break;
            

            //交换
            swap(arr, l, r);

            //如果(交换后)左值等于了中间值,说明中间值左边全部小于中间值,则无需在移动,移动右值
            if (arr[l] == pivot) 
                r--;
            
            //同理,移动左值,避免特殊情况(多个等于中间值)
            if (arr[r] == pivot) 
                l++;
            
        //退出循环时则完成了 左边值 <= 基准值 <= 右边值

        //如果退出循环两个值相等则分别向另一个位置移动一格,以便递归
        if (l == r) 
            l++;
            r--;
        

        //右递归
        if (l < right) 
            sort2(arr, l, right);
        

        //左递归
        if (left < r) 
            sort2(arr, left, r);
        

    

    //交换
    public static void swap(int[] arr, int x, int y) 
        int temp = arr[x];
        arr[x] = arr[y];
        arr[y] = temp;
    

4.6 归并排序

4.6.1 介绍

归并排序（MERGE-SORT）是利用归并的思想实现的排序方法，该算法采用经典的分治（divide-and-conquer）策略（分治法将问题分(divide)成一些小的问题然后递归求解，而治(conquer)的阶段则将分的阶段得到的各答案"修补"在一起，即分而治之)。

4.6.2 算法步骤

• 申请空间，使其大小为两个已经排序序列之和，该空间用来存放合并后的序列；
• 设定两个指针，最初位置分别为两个已经排序序列的起始位置；
• 比较两个指针所指向的元素，选择相对小的元素放入到合并空间，并移动指针到下一位置；
• 重复步骤 3 直到某一指针达到序列尾；
• 将另一序列剩下的所有元素直接复制到合并序列尾。

4.6.3 动画演示

4.6.4 java 代码实现和数据测试

/**
 * @author 谢阳
 * @version 1.8.0_131
 */
public class MergeSort 
    public static void main(String[] args) 
        int[] arr = new int[80000];
        for (int i = 0; i < 80000; i++) 
            arr[i] = (int) (Math.random() * 1000000);
        
        long time = System.currentTimeMillis();
        mergeSort(arr, 0, arr.length - 1);//time = 26 time = 29 time = 28
        System.out.println("time = " + (System.currentTimeMillis() - time));
        //int[] arr = 8, 4, 5, 7, 1, 3, 6;
        //mergeSort(arr, 0, arr.length - 1);
        //System.out.println(Arrays.toString(arr));

    

    //归并排序
    public static void mergeSort(int arr[], int left, int right) 
        //判断当前数组的长度是否满足要求(大于1)
        if (left < right) 
            //中间值
            int mid = (left + right) / 2;
            //分治,将一个大数组分成两个小数组
            mergeSort(arr, left, mid);
            mergeSort(arr, mid + 1, right);

            //合并,递归的最底层为两个数据,向上回溯
            merge(arr, left, mid, right);
        
    

    //合并(两个数组)数据并排序
    public static void merge(int[] arr, int left, int mid, int right) 
        //用i、j表示两个数组开始的起始坐标
        int i = left;//[left,mid]
        int j = mid + 1;//[mid+1,right]

        //创建存放数据的临时数组空间,大小为(right - left) + 1
        int[] temp = new int[(right - left) + 1];

        //temp的起始位置
        int t = 0;

        //两个有序数组比较数据大小,按顺序将数据放入临时数组中,如果其中一个数组放置完成则退出循环
        while (i <= mid && j <= right) 
            temp[t++] = arr[i] < arr[j] ? arr[i++] : arr[j++];
        

        //如果数组未遍历完则将剩余数据添加到 temp 后面
        while (i <= mid) 
            temp[t++] = arr[i++];
        

        //同上
        while (j <= right) 
            temp[t++] = arr[j++];
        
        //System.out.println("left = " + left + "\\tright = " + right);

        t = 0;//恢复temp起始位置

        //将合并的有序数据覆盖掉原有数据
        while (left <= right) 
            arr[left++] = temp[t++];
        
    

4.7 基数排序

4.7.1 介绍

基数排序（radix sort）属于“分配式排序”（distribution sort），又称“桶子法”（bucket sort）或bin sort，顾名思义，它是通过键值的各个位的值，将要排序的元素分配至某些“桶”中，达到排序的作用

4.7.2 算法步骤

• 事先准备10个数组(10个桶)， 0-9 分别对应 位数的 0-9
• 第一轮按照个位大小 放入到 对应的 各个数组中
• 然后从 0-9 个数组/桶，依次，按照加入元素的先后顺序取出
• 第二轮按照十位排序，将各个数，按照十位大小 放入到 对应的 各个数组中
• 然后从 0-9 个数组/桶，依次，按照加入元素的先后顺序取出
• 重复上述炒作直至最大数位数为止

4.7.3 动画演示

4.7.4 java 代码实现和数据测试

import java.util.Arrays;

/**
 * @author 谢阳
 * @version 1.8.0_131
 */
public class RadixSort 
    public static void main(String[] args) 
        int[] arr = new int[80000];
        for (int i = 0; i < 80000; i++) 
            arr[i] = (int) (Math.random() * 1000000);
        
        long time = System.currentTimeMillis();
        radixSort(arr);
        //time = 31 time = 21 time = 26 数据量越大效果越明显
        System.out.println("time = " + (System.currentTimeMillis() - time));
        //int[] arr = 53, 3, 542, 748, 14, 214, 9999, 12, 10000, 0;
        //radixSort(arr);
        //System.out.println(Arrays.toString(arr));

    

    //基数排序
    public static void radixSort(int[] arr) 
        //获取数组长度
        int len = arr.length;

        //获取数组中最大值
        int maxValue = getMaxValue(arr, len);

        //获取该数的长度
        int valueLength = getValueLength(maxValue);

        //创建放数的桶,10 表示 0~9 号桶
        int[][] bucket = new int[10][len];

        //创建统计每个桶中数据对应的计数器
        int[] preBucketCount = new int[10];

        //创建记录数据所在桶的坐标记录
        int bucketIndex;

        //循环valueLength次,dev是决定每次排序按相应规则(个、十、百等)排序
        for (int i = 0, dev = 1; i < valueLength; i++, dev *= 10) 

            //遍历放入对应桶中
            for (int j = 0; j < len; j++) 
                bucketIndex = arr[j] / dev % 10;//个位、十位、百位...
                bucket[bucketIndex][preBucketCount[bucketIndex]] = arr[j];
                //计数器大小等于值的个数
                preBucketCount[bucketIndex]++;
            

            int index = 0;

            //遍历桶中数据并覆盖掉原有数据
            for (int j = 0; j < bucket.length; j++) 
                for (int k = 0; k < preBucketCount[j]; k++) 
                    arr[index++] = bucket[j][k];
                
                //将计数清零
                preBucketCount[j] = 0;
            
        

    

    //得到数组中最大值
    public static int getMaxValue(int[] arr, int len) 
        if (len == 0) 
            return 0;
        

        int max = arr[0];
        for (int i = 1; i < arr.length; i++) 
            if (max < arr[i]) 
                max = arr[i];
            
        

        return max;
    

    //计算数值的长度
    public static int getValueLength(int value) 
        int count = 0;
        while (value != 0) 
            count++;
            value /= 10;
        

        return count;
    

4.8 堆排序

4.8.1 介绍

堆排序是利用堆这种数据结构而设计的一种排序算法，堆排序是一种选择排序，它的最坏，最好，平均时间复杂度均为O(nlogn)，它也是不稳定排序。堆是具有以下性质的完全二叉树：每个结点的值都大于或等于其左右孩子结点的值，称为大顶堆, 注意 : 没有要求结点的左孩子的值和右孩子的值的大小关系。每个结点的值都小于或等于其左右孩子结点的值，称为小顶堆

4.8.2 算法步骤

• 创建一个堆 H[0……n-1]；
• 把堆首（最大值）和堆尾互换；
• 把堆的尺寸缩小 1，并调用 shift_down(0)，目的是把新的数组顶端数据调整到相应位置；
• 重复步骤 2，直到堆的尺寸为 1。

4.8.3 动画演示

4.8.4 java 代码实现和数据测试

/**
 * @author 谢阳
 * @version 1.8.0_131
 */
public class HeapSort 
    public static void main(String[] args) 
        int[] arr = new int[80000];
        for (int i = 0; i < 80000; i++) 
            arr[i] = (int) (Math.random() * 1000000);
        
        long time = System.currentTimeMillis();
        heapSort(arr);//time = 10  time = 10 time = 17
        System.out.println("time = " + (System.currentTimeMillis() - time));
        //int[] arr = 1, 2, -1, 3, 999, -2, 4, 5, 6, 7, 8, 16, 9;
        //heapSort(arr);
        //System.out.println(Arrays.toString(arr));

    

    public static void heapSort(int[] arr) 
        int len = arr.length;
        //调整为大顶堆
        for (int i = len / 2 - 1; i >= 0; i--) 
            adjustHeap(arr, i, len);
        
        int temp;
        while (len > 1) 
            //交换
            temp = arr[0];
            arr[0] = arr[len - 1];
            arr[len - 1] = temp;
            len--;
            //调整节点
            adjustHeap(arr, 0, len);
        

    

    //调整大节点在上面
    public static void adjustHeap(int[] arr, int i, int length) 
        //定义变量存储节点值
        int temp = arr[i];

        //遍历是该节点和下面所有节点成为以该节点为中心的大顶堆
        for (int k = i * 2 + 1; k < length; k = k * 2 + 1) 
            //使arr[k]为该节点temp下面的最大值
            if (k + 1 < length && arr[k] < arr[k + 1]) 
                k++;
            
            //判断arr[k]是否大于temp,大于则交换位置
            if (arr[k] > temp) 
                arr[i] = arr[k];
                i = k;
             else //其他情况则排序好了
                break;
            
        

        arr[i] = temp;
    

参考资料

菜鸟教程

尚硅谷Java数据结构与java算法（Java数据结构与算法）