模型推理谈谈 caffe 的 bn 和 scale 算子
Posted 极智视界
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了模型推理谈谈 caffe 的 bn 和 scale 算子相关的知识,希望对你有一定的参考价值。
欢迎关注我的公众号 [极智视界],获取我的更多笔记分享
O_o >_< o_O O_o ~_~ o_O
本文聊一聊 caffe 的 bn 和 scale 算子。
caffe 中的 bn 算子和其他框架如 pytorch、darknet 中的有点区别,故这里拎出来聊一聊,避免大家走坑。前面也写过一篇关于 bn 的文章,有兴趣的同学可以查阅 《【模型推理】从部署的角度看 bn 和 in 算子》。
这里主要聊一下 caffe 中的 bn 相比于其他框架有什么区别,以及 caffe 框架中对于 bn 的 cpu 和 gpu 的前向推理实现。
1、caffe bn 的特殊之处
在我的文章《【模型推理】从部署的角度看 bn 和 in 算子》中有写过,整个 bn 算子的计算过程数学表达如下:

基本过程是:
(1) 求均值;
(2) 求方差;
(3) 归一化;
(4) 缩放和偏置;
其中,(1) 求均值 和 (2) 求方差的过程在训练的时候就做了,所以对于推理来说就只要加载离线的权重就好了。来说一下 caffe 中的 bn 有什么不一样,caffe 中的 bn 其实只做了 (3) 归一化,而 (4) 缩放和偏置 由 scale 算子来做,所以整个 bn 的计算在 caffe 里是需要 bn + scale 两个算子来实现的,这和其他框架如 pytorch 或 darknet 里是不一样的。
来对比一下 netron 的网络结构会更加直观,先来看一下 pytorch 的 conv + bn + activation 块,可以看到三个算子是拆开的,比较有条理,bn 也是完整的 bn。

来看一下 onnx 的样子,onnx 的算子粒度比较细,这里把 activation 拆开了,实际 bn 还是完整的 bn。
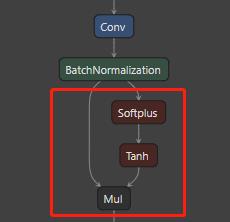
再来看一下 darknet,可以看到 darknet 中的 bn 是默认写在 conv 里的,所以在 darknet 里 conv + bn + activation (请自动忽略这里的激活不是 relu,我随便找了个) 是一个融合大算子,由 batch_normalize 标志位来决定是否有 bn,同样这里的 bn 是完整的 bn。

最后再来看一下 caffe 里的 conv + bn + activation 块,可以看到 caffe 里的情况不太一样,bn 会被拆成 BatchNorm + Scale,所以 conv + bn + activation 块在 caffe 里是 conv + bn + scale + activation。这里的 bn 不是完整的 bn,这就是 caffe 中的 bn 和 其他框架中的 bn 不一样的地方。

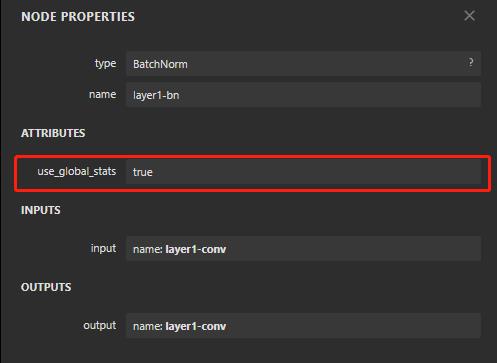
再来深入看一下 caffe 里 bn 的参数,可以看到 bn 里有个参数 use_global_stats,这个参数的意思是值为真,就使用保存的 均值 和 方差,否则使用滑动平均计算新的 均值 和 方差,这里的 bn 其实只做归一化。
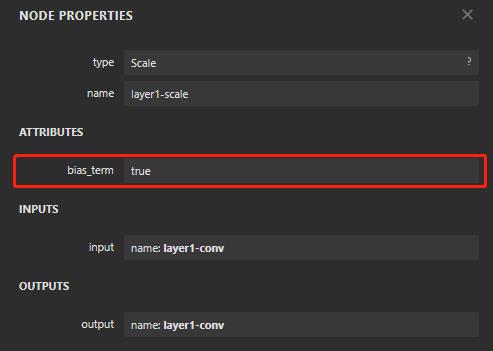
来看一下 scale 的参数,看到 bias_term 这个参数的时候,也许你会恍然大悟,一般的 scale 只做缩放,带 bias 的 scale 会做 缩放 + 偏置,当把这个和上面 bn 的归一化过程结合起来,其实就是一个完整的 bn 过程。
下面结合 caffe 源码说一下。
2、caffe bn forward_cpu 实现
先看 caffe.proto 里的 BatchNormParameter,源码里注释很多,为了看起来简洁,我这里把注释扔了,如下:
message BatchNormParameter {
optional bool use_global_stats = 1;
optional float moving_average_fraction = 2 [default = .999];
optional float eps = 3 [default = 1e-5];
}
可以看到有三个超参,其中 use_global_stats 上面提到过,用来定义是否直接使用离线 均值 和 方差 权重,moving_average_fraction 为滑动平均系数,如果 use_global_stats 为真,则用不上 moving_average_fraction,否则就用 moving_average_fraction 来更新均值。eps 是一个防止分母为零的超参。
来看一下 bn 的头,我这里把命名空间 caffe 给省略了:
template <typename Dtype>
class BatchNormLayer : public Layer<Dtype> {
public:
explicit BatchNormLayer(const LayerParameter& param)
: Layer<Dtype>(param) {}
virtual void LayerSetUp(const vector<Blob<Dtype>*>& bottom,
const vector<Blob<Dtype>*>& top);
virtual void Reshape(const vector<Blob<Dtype>*>& bottom,
const vector<Blob<Dtype>*>& top);
virtual inline const char* type() const { return "BatchNorm"; }
virtual inline int ExactNumBottomBlobs() const { return 1; }
virtual inline int ExactNumTopBlobs() const { return 1; }
protected:
virtual void Forward_cpu(const vector<Blob<Dtype>*>& bottom,
const vector<Blob<Dtype>*>& top);
virtual void Forward_gpu(const vector<Blob<Dtype>*>& bottom,
const vector<Blob<Dtype>*>& top);
virtual void Backward_cpu(const vector<Blob<Dtype>*>& top,
const vector<bool>& propagate_down, const vector<Blob<Dtype>*>& bottom);
virtual void Backward_gpu(const vector<Blob<Dtype>*>& top,
const vector<bool>& propagate_down, const vector<Blob<Dtype>*>& bottom);
Blob<Dtype> mean_, variance_, temp_, x_norm_;
bool use_global_stats_;
Dtype moving_average_fraction_;
int channels_;
Dtype eps_;
// extra temporarary variables is used to carry out sums/broadcasting
// using BLAS
Blob<Dtype> batch_sum_multiplier_;
Blob<Dtype> num_by_chans_;
Blob<Dtype> spatial_sum_multiplier_;
};
BatchNormLayer 算子类里声明了几个关键的函数:Forward_cpu、Forward_gpu、Backward_cpu、Backward_gpu,其中 Backward 主要用于训练梯度反传,对于推理我们不关心。先来看一下 Forward_cpu,实现其实也比较简单,加载 均值 和 方差,按 use_global_stats_ 是否为真来分为两块,如果 为真,非常简单,直接加载 均值 和 方差,推理的话走这个 flow 就可以了;如果为否则用 滑动平均 先计算 均值,再根据这个均值来更新方差,这个一般用于训练的时候更新 均值 和 方差。
先来说一下这个滑动平均更新 均值 和 方差,训练的过程并不是一次前向计算就结束,而是从总样本中抽取 mini-batch 个样本,进行多次前向计算,这样的话需要考虑每次计算得到的 均值 和 方差 怎么结合,caffe 里的算法并不是简简单单的将每次计算的 均值 和 方差 累加,而是把前一次计算的 均值 和 方差 的影响减小(乘以一个小于1的变量),再加上本次计算的结果,即所谓的 滑动平均更新方式。
前向计算均值代码如下:
if (use_global_stats_) {
// use the stored mean/variance estimates.
const Dtype scale_factor = this->blobs_[2]->cpu_data()[0] == 0 ?
0 : 1 / this->blobs_[2]->cpu_data()[0];
caffe_cpu_scale(variance_.count(), scale_factor,
this->blobs_[0]->cpu_data(), mean_.mutable_cpu_data());
caffe_cpu_scale(variance_.count(), scale_factor,
this->blobs_[1]->cpu_data(), variance_.mutable_cpu_data());
} else {
// compute mean
caffe_cpu_gemv<Dtype>(CblasNoTrans, channels_ * num, spatial_dim,
1. / (num * spatial_dim), bottom_data,
spatial_sum_multiplier_.cpu_data(), 0.,
num_by_chans_.mutable_cpu_data());
caffe_cpu_gemv<Dtype>(CblasTrans, num, channels_, 1.,
num_by_chans_.cpu_data(), batch_sum_multiplier_.cpu_data(), 0.,
mean_.mutable_cpu_data());
}
然后根据这个计算出来的 均值 来计算 方差,整个代码就复杂在这里。
if (!use_global_stats_) {
// compute variance using var(X) = E((X-EX)^2)
caffe_sqr<Dtype>(top[0]->count(), top_data,
temp_.mutable_cpu_data()); // (X-EX)^2
caffe_cpu_gemv<Dtype>(CblasNoTrans, channels_ * num, spatial_dim,
1. / (num * spatial_dim), temp_.cpu_data(),
spatial_sum_multiplier_.cpu_data(), 0.,
num_by_chans_.mutable_cpu_data());
caffe_cpu_gemv<Dtype>(CblasTrans, num, channels_, 1.,
num_by_chans_.cpu_data(), batch_sum_multiplier_.cpu_data(), 0.,
variance_.mutable_cpu_data()); // E((X_EX)^2)
// compute and save moving average
this->blobs_[2]->mutable_cpu_data()[0] *= moving_average_fraction_;
this->blobs_[2]->mutable_cpu_data()[0] += 1;
caffe_cpu_axpby(mean_.count(), Dtype(1), mean_.cpu_data(),
moving_average_fraction_, this->blobs_[0]->mutable_cpu_data());
int m = bottom[0]->count()/channels_;
Dtype bias_correction_factor = m > 1 ? Dtype(m)/(m-1) : 1;
caffe_cpu_axpby(variance_.count(), bias_correction_factor,
variance_.cpu_data(), moving_average_fraction_,
this->blobs_[1]->mutable_cpu_data());
}
下面来看归一化的过程,减均值:
// subtract computed_mean
caffe_cpu_gemm<Dtype>(CblasNoTrans, CblasNoTrans, num, channels_, 1, 1,
batch_sum_multiplier_.cpu_data(), mean_.cpu_data(), 0.,
num_by_chans_.mutable_cpu_data());
caffe_cpu_gemm<Dtype>(CblasNoTrans, CblasNoTrans, channels_ * num,
spatial_dim, 1, -1, num_by_chans_.cpu_data(),
spatial_sum_multiplier_.cpu_data(), 1., top_data);
这里怎么就实现了减均值的操作呢,来看一下 caffe_cpu_gemm 做了什么:
template<>
void caffe_cpu_gemm<float>(const CBLAS_TRANSPOSE TransA,
const CBLAS_TRANSPOSE TransB, const int M, const int N, const int K,
const float alpha, const float* A, const float* B, const float beta,
float* C) {
int lda = (TransA == CblasNoTrans) ? K : M;
int ldb = (TransB == CblasNoTrans) ? N : K;
cblas_sgemm(CblasRowMajor, TransA, TransB, M, N, K, alpha, A, lda, B,
ldb, beta, C, N);
}
caffe_cpu_gemm 的功能是矩阵乘,即 C=alpha*A*B+beta*C,其中 A,B,C 是输入矩阵(一维数组格式);CblasRowMajor : 数据是行主序的(二维数据也是用一维数组储存的);TransA, TransB:是否要对A和B做转置操作(CblasTrans CblasNoTrans);M: A、C 的行数;N: B、C 的列数;K: A 的列数, B 的行数;lda : A的列数(不做转置)行数(做转置);ldb: B的列数(不做转置)行数(做转置)。所以:
/// 原计算
caffe_cpu_gemm<Dtype>(CblasNoTrans, CblasNoTrans, num, channels_, 1, 1,
batch_sum_multiplier_.cpu_data(), mean_.cpu_data(), 0.,
num_by_chans_.mutable_cpu_data());
/// 相当于
num_by_chans_.mutable_cpu_data() = batch_sum_multiplier_.cpu_data() * mean_.cpu_data()
/// 原计算
caffe_cpu_gemm<Dtype>(CblasNoTrans, CblasNoTrans, channels_ * num,
spatial_dim, 1, -1, num_by_chans_.cpu_data(),
spatial_sum_multiplier_.cpu_data(), 1., top_data);
/// 相当于
top_data = - num_by_chans_.cpu_data() * spatial_sum_multiplier_.cpu_data() + top_data
/// 而 top_data 是什么呢,之前源码里有一句
if (bottom[0] != top[0]) {
caffe_copy(bottom[0]->count(), bottom_data, top_data);
}
这样就比较清楚了。
接下来给方差进行平滑,并开标准差:
// normalize variance
caffe_add_scalar(variance_.count(), eps_, variance_.mutable_cpu_data());
caffe_sqrt(variance_.count(), variance_.cpu_data(),
variance_.mutable_cpu_data());
其中 caffe_add_scalar 的实现如下,就是给每个 Y 加上一个 alpha。结合我们这里就是给每个方差加上一个很小的 eps,防止它为 0。caffe_sqrt 就不用多说了,就是开方,所以经过了这波操作后就得到了标准差,存放在这里 variance_.cpu_data()。
template <>
void caffe_add_scalar(const int N, const float alpha, float* Y) {
for (int i = 0; i < N; ++i) {
Y[i] += alpha;
}
}
最后做归一化,前面讲到有两个比较重要的存储数据的变量,减均值后 feature_map 数据放在这 top_data,标准差放在这 variance_.cpu_data(),带着这两个记忆来看代码:
// replicate variance to input size
caffe_cpu_gemm<Dtype>(CblasNoTrans, CblasNoTrans, num, channels_, 1, 1,
batch_sum_multiplier_.cpu_data(), variance_.cpu_data(), 0.,
num_by_chans_.mutable_cpu_data());
caffe_cpu_gemm<Dtype>(CblasNoTrans, CblasNoTrans, channels_ * num,
spatial_dim, 1, 1., num_by_chans_.cpu_data(),
spatial_sum_multiplier_.cpu_data(), 0., temp_.mutable_cpu_data());
caffe_div(temp_.count(), top_data, temp_.cpu_data(), top_data);
// TODO(cdoersch): The caching is only needed because later in-place layers
// might clobber the data. Can we skip this if they won't?
caffe_copy(x_norm_.count(), top_data,
x_norm_.mutable_cpu_data());
比较关键的是:
caffe_div(temp_.count(), top_data, temp_.cpu_data(), top_data);
来看一下 caffe_div 的实现,即做 element-wise 的除法,所以很好理解,就是拿 减均值后的数据 除以 标准差,至此完成了归一化操作。
template <>
void caffe_div<float>(const int n, const float* a, const float* b,
float* y) {
vsDiv(n, a, b, y);
}
caffe 源码中的 bn forward_cpu 到这里就结束了,可以看到只有归一化操作,没有缩放和偏置的操作,这也进一步验证了 caffe 中的 bn 是拆成 bn + scale 来做的。
3、caffe bn forward_cuda 实现
高性能计算离不开 cuda,让我们一起来看下 caffe bn forward_cuda 的实现代码。其实逻辑很简单,我把整个代码贴上先:
template <typename Dtype>
void BatchNormLayer<Dtype>::Forward_gpu(const vector<Blob<Dtype>*>& bottom,
const vector<Blob<Dtype>*>& top) {
const Dtype* bottom_data = bottom[0]->gpu_data();
Dtype* top_data = top[0]->mutable_gpu_data();
int num = bottom[0]->shape(0);
int spatial_dim = bottom[0]->count()/(channels_*bottom[0]->shape(0));
if (bottom[0] != top[0]) {
caffe_copy(bottom[0]->count(), bottom_data, top_data);
}
if (use_global_stats_) {
// use the stored mean/variance estimates.
const Dtype scale_factor = this->blobs_[2]->cpu_data()[0] == 0 ?
0 : 1 / this->blobs_[2]->cpu_data()[0];
caffe_gpu_scale(variance_.count(), scale_factor,
this->blobs_[0]->gpu_data(), mean_.mutable_gpu_data());
caffe_gpu_scale(variance_.count(), scale_factor,
this->blobs_[1]->gpu_data(), variance_.mutable_gpu_data());
} else {
// compute mean
caffe_gpu_gemv<Dtype>(CblasNoTrans, channels_ * num, spatial_dim,
1. / (num * spatial_dim), bottom_data,
spatial_sum_multiplier_.gpu_data(), 0.,
num_by_chans_.mutable_gpu_data());
caffe_gpu_gemv<Dtype>(CblasTrans, num, channels_, 1.,
num_by_chans_.gpu_data(), batch_sum_multiplier_.gpu_data(), 0.,
mean_.mutable_gpu_data());
}
// subtract mean
caffe_gpu_gemm<Dtype>(CblasNoTrans, CblasNoTrans, num, channels_, 1, 1,
batch_sum_multiplier_.gpu_data(), mean_.gpu_data(), 0.,
num_by_chans_.mutable_gpu_data());
caffe_gpu_gemm<Dtype>(CblasNoTrans, CblasNoTrans, channels_ * num,
spatial_dim, 1, -1, num_by_chans_.gpu_data(),
spatial_sum_multiplier_.gpu_data(), 1., top_data);
if (!use_global_stats_) {
// compute variance using var(X) = E((X-EX)^2)
caffe_gpu_mul(top[0]->count(), top[0]->gpu_data(), top[0]->gpu_data(),
temp_.mutable_gpu_data()); // (X-EX)^2
caffe_gpu_gemv<Dtype>(CblasNoTrans, channels_ * num, spatial_dim,
1. / (num * spatial_dim), temp_.gpu_data(),
spatial_sum_multiplier_.gpu_data(), 0.,
num_by_chans_.mutable_gpu_data());
caffe_gpu_gemv<Dtype>(CblasTrans, num, channels_, Dtype(1.),
num_by_chans_.gpu_data(), batch_sum_multiplier_.gpu_data(), Dtype(0.),
variance_.mutable_gpu_data()); // E((X_EX)^2)
// compute and save moving average
this->blobs_[2]->mutable_cpu_data()[0] *= moving_average_fraction_;
this->blobs_[2]->mutable_cpu_data()[0] += 1;
caffe_gpu_axpby(mean_.count(), Dtype(1), mean_.gpu_data(),
moving_average_fraction_, this->blobs_[0]->mutable_gpu_data());
int m = bottom[0]->count()/channels_;
Dtype bias_correction_factor = m > 1 ? Dtype(m)/(m-1) : 1;
caffe_gpu_axpby(variance_.count(), bias_correction_factor,
variance_.gpu_data(), moving_average_fraction_,
this->blobs_[1]->mutable_gpu_data());
}
// normalize variance
caffe_gpu_add_scalar(variance_.count(), eps_, variance_.mutable_gpu_data());
caffe_gpu_sqrt(variance_.count(), variance_.gpu_data(),
variance_.mutable_gpu_data());
// replicate variance to input size
caffe_gpu_gemm<Dtype>(CblasNoTrans, CblasNoTrans, num, channels_, 1, 1,
batch_sum_multiplier_.gpu_data(), variance_.gpu_data(), 0.,
num_by_chans_.mutable_gpu_data());
caffe_gpu_gemm<Dtype>(CblasNoTrans, CblasNoTrans, channels_ * num,
spatial_dim, 1, 1., num_by_chans_.gpu_data(),
spatial_sum_multiplier_.gpu_data(), 0., temp_.mutable_gpu_data());
caffe_gpu_div(temp_.count(), top_data, temp_.gpu_data(), top_data);
// TODO(cdoersch): The caching is only needed because later in-place layers
// might clobber the data. Can we skip this if they won't?
caffe_copy(x_norm_.count(), top_data,
x_norm_.mutable_gpu_data());
}
我们来看一下 bn forward_gpu 和 forward_cpu 有什么区别,逻辑上可以说是一毛一样,函数传参也是一毛一样,拿 beyond compare 简单直观对比一下,你看区别都是些啥,caffe_gpu_scale、caffe_gpu_gemv、caffe_gpu_gemm…

所以我觉得 caffe bn forward_gpu 代码没啥好说的,参考 forward_cpu 就可以。
收工了,有问题欢迎讨论~
【公众号传送】
扫描下方二维码即可关注我的微信公众号【极智视界】,获取更多AI经验分享,让我们用极致+极客的心态来迎接AI !

以上是关于模型推理谈谈 caffe 的 bn 和 scale 算子的主要内容,如果未能解决你的问题,请参考以下文章