❤️《算法和数据结构》小白零基础教学，三十张彩图，C语言配套代码，之 二叉树详解❤️(建议收藏)

Posted 2021-10-10 英雄哪里出来

本文已收录于专栏 🌳《画解数据结构》🌳

前言

  「 数据结构 」 和 「 算法 」 是密不可分的，两者往往是「 相辅相成 」的存在，所以，在学习 「 数据结构 」 的过程中，不免会遇到各种「 算法 」。
  数据结构 常用的操作一般为：「 增 」「 删 」「 改 」「 查 」。
  这篇文章，作者将用 「 X张动图 」 来阐述一种 「 树形 」 的数据结构

「 二叉树 」

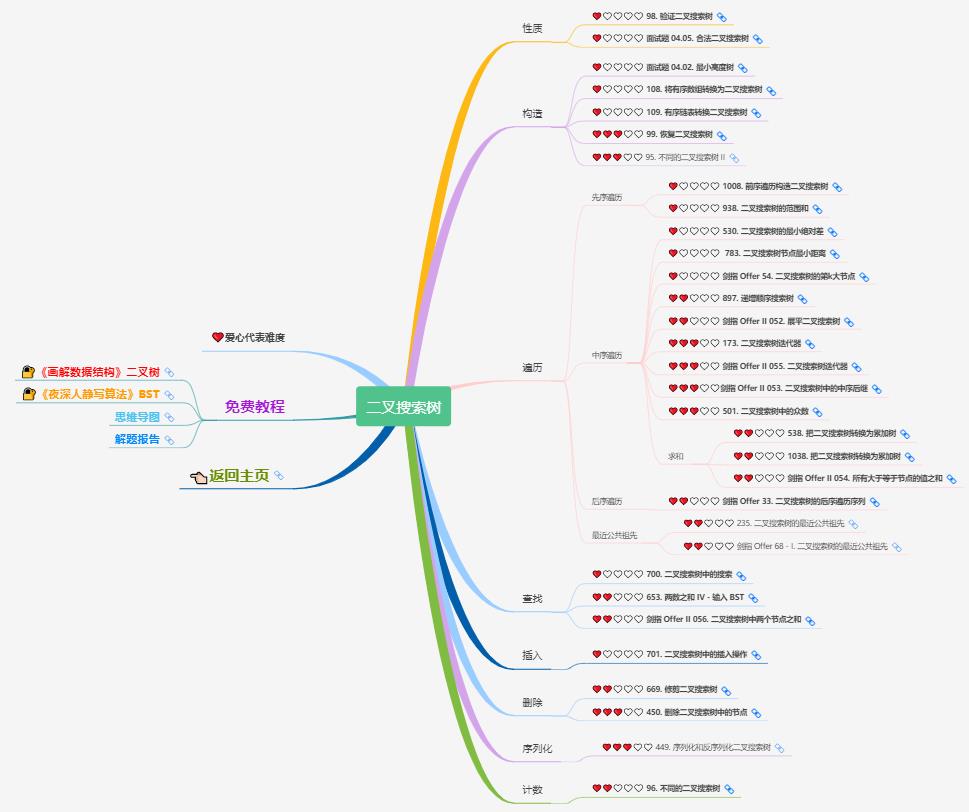
  这篇文章的主要目的是讲解二叉树的一些基础概念，以及和二叉树相关的一些经典遍历算法。但是实际学习过程还是需要看个人的毅力和坚持。下图代表的是 LeetCode 经典的二叉搜索树的题集，其中树是很重要的一个章节，涉及了诸多算法，希望可以供读者参考和学习。

点击我跳转末尾 获取 粉丝专属 《算法和数据结构》源码。

文章目录

• 前言
• 一、树的概念
• • 1、树的定义
  • • 1）树
    • 2）空树
    • 3）子树
  • 2、结点的定义
  • • 1）根结点
    • 2）叶子结点
    • 3）内部结点
  • 3、结点间关系
  • • 1）孩子结点
    • 2）父结点
    • 3）兄弟结点
  • 4、树的深度
  • 5、森林的定义
• 二、树的表示法
• • 1、父亲表示法
  • • 1）存储方式
    • 2）源码详解
    • 3）图片剖析
    • 4）结构剖析
  • 2、孩子表示法
  • • 1）存储方式
    • 2）源码详解
    • 3）图片剖析
    • 4）结构剖析
  • 3、左儿子右兄弟
  • • 1）存储方式
    • 2）源码详解
    • 3）图片剖析
    • 4）结构剖析
• 三、二叉树的概念
• • 1、二叉树的性质
  • 2、特殊二叉树
  • • 1）斜树
    • 2）满二叉树
    • 2）完全二叉树
  • 3、二叉树的性质
  • • 1）性质1
    • 2）性质2
    • 3）性质3
    • 4）性质4
• 四、二叉树的存储
• • 1、顺序表存储
  • • 1）完全二叉树
    • 2）非完全二叉树
    • 3）稀疏二叉树
  • 2、链表存储
• 五、二叉树的遍历
• • 1、 前序遍历
  • • 1）算法描述
    • 2）源码详解
  • 2、 中序遍历
  • • 1）算法描述
    • 2）源码详解
  • 3、 后序遍历
  • • 1）算法描述
    • 2）源码详解
  • 4、 层序遍历
  • • 1）算法描述
• 粉丝专属福利

一、树的概念

1、树的定义

1）树

  树是 $n(n\ge 0)$ 个结点的有限集合。当 $n>0$ 时，它是一棵非空树，满足如下条件：
    1）有且仅有一个特定的结点，称为根结点 $Root$；
    2）除根结点外，其余结点分为 $m$ 个互不相交的有限集合 $T_1$、$T_2$、$\dots \dots$、$T_m$，其中每一个 $T_i(1\le i\le m)$ 又是一棵树，并且为 根结点 $Root$ 的子树。如图所示，代表的是一棵以 $a$ 为根结点的树。

2）空树

  当 $n=0$，也就是 $0$ 个结点的情况也是树，它被称为空树。

3）子树

  树的定义用到了递归的思想。即树的定义中还是用到了树的概念，如图所示，$T_1$ 和 $T_2$ 就是结点 $a$ 的子树。结点 $d$、$g$、$h$、$i$ 组成的树又是结点 $b$ 的子树等等。

  子树的个数没有限制，但是它们一定是互不相交的，如下图所示的就不是树。因为在这两个图中，$a$ 的子树都有相交的边。

2、结点的定义

  树的结点包含一个 数据域 和 $m$ 个 指针域 用来指向它的子树。结点的种类分为：根结点、叶子结点、内部结点。结点拥有子树的个数被称为 结点的度。树中各个结点度的最大值被称为 树的度。

1）根结点

  一棵树的根结点只有一个。

2）叶子结点

  度为 0 的结点被称为 叶子结点 或者 终端结点。叶子结点的不指向任何子树。

3）内部结点

  除了根结点和叶子结点以外的结点，被称为内部结点。

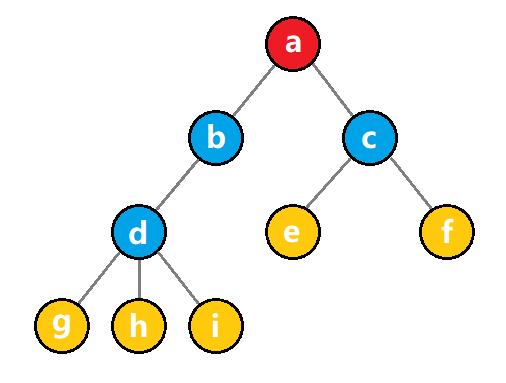
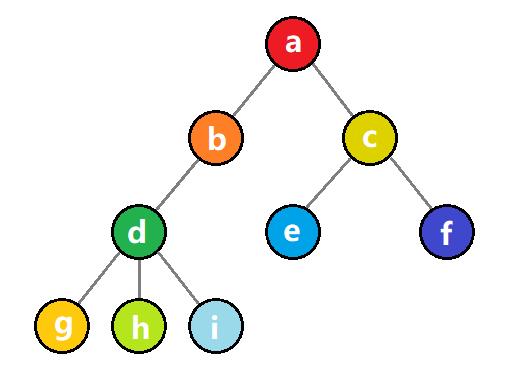
  如上图所示，红色结点 为根结点，蓝色结点 为内部结点，黄色结点 为叶子结点。

3、结点间关系

1）孩子结点

  对于某个结点，它的子树的根结点，被称为该结点的 孩子结点。

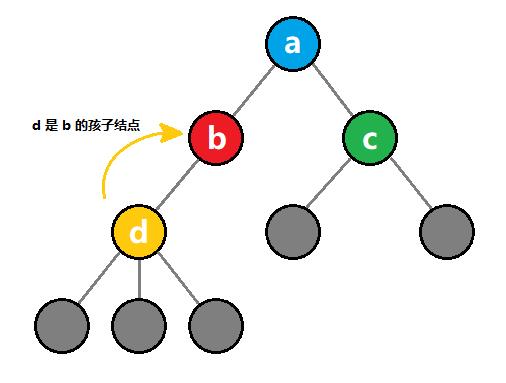
  如上图所示，黄色结点 d 是 红色结点 b 的孩子结点。

2）父结点

  而该结点被称为孩子结点的 父结点。

  如上图所示，蓝色结点 a 是 红色结点 b 的父结点。

3）兄弟结点

  同一父结点下的孩子结点，互相称为 兄弟结点。

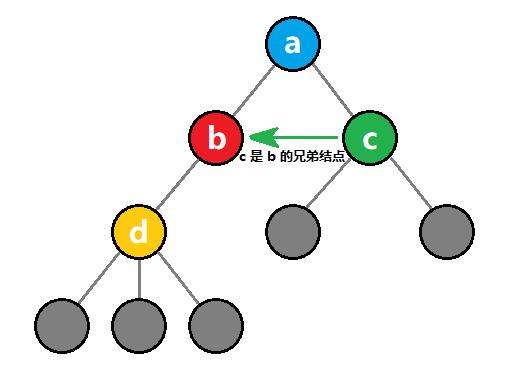
  如上图所示，绿色结点 c 和 红色结点 b 互为兄弟结点。

4、树的深度

  结点的层次从根结点开始记为第 1 层，如果某结点在第 $i$ 层，则它的子树的根结点就在 第 $i+1$ 层，树中结点的最大层次称为 树的深度。
  如下图所示，代表的是一棵深度为 4 的树。

5、森林的定义

  森林是 $m$ 棵 互不相交的树的集合，对于树的每个结点而言，其子树集合就是森林。
  如图所示，$b$ 和 $c$ 两棵子树组成的集合就是一个森林。

二、树的表示法

1、父亲表示法

1）存储方式

  除了根结点以外，树上的每个结点都会 有且仅有 一个父结点。所以，我们可以将每个结点定义成结构体，总共两个成员：数据域 和 父结点域。并且把每个结点连续的存储到结构体数组中， 父结点域 指向的是数组下标，当没有父结点时，值为 $-1$。

2）源码详解

#define MAXN 1024          // (1)
#define DataType int       // (2)
typedef struct  {
    DataType data;         // (3)
    int parent;            // (4)
}TreeNode; 

typedef struct  {
    TreeNode nodes[MAXN];  // (5)
    int root;              // (6)
    int n;                 // (7)
}Tree;

• $(1)$ MAXN代表了最多允许的结点数量；
• $(2)$ DataType表示结点 数据域 的类型；
• $(3)$ data代表了树结点TreeNode的 数据域；
• $(4)$ parent代表了树结点的 父结点域，它是Tree这个结构体中nodes[]数组的下标；
• $(5)$ nodes[MAXN]存储了树的所有结点，是一个数组，可以通过下标进行索引；
• $(6)$ root代表了这棵树的 根结点 的下标；
• $(7)$ n代表当前有多少 树结点；

3）图片剖析

  下图代表了一棵完整的树，[0]代表第 0 号结点，它的数据域为 $a$，其中 0 为数组下标；[1]代表第 1 号结点，它的数据域为 $b$，以此类推。

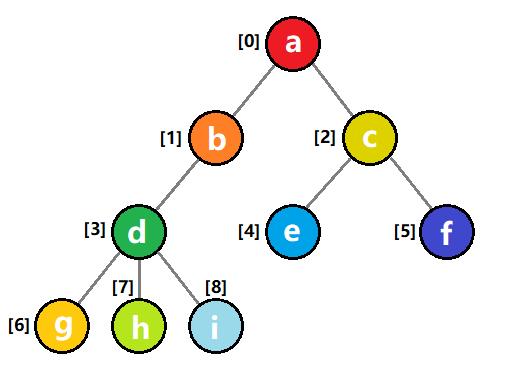
  结构体数组存储如下：

下标	data	parent
0	$a$	$-1$
1	$b$	$0$
2	$c$	$0$
3	$d$	$1$
4	$e$	$2$
5	$f$	$2$
6	$g$	$3$
7	$h$	$3$
8	$i$	$3$

4）结构剖析

  这种存储结构中，通过结点获取 父结点 的时间复杂度为 $O(1)$。但是，如果想要知道某个结点有哪些孩子结点，则必须遍历整棵树才行。

2、孩子表示法

1）存储方式

  父亲表示法无法知道某个结点有哪些孩子结点，所以我们可以对它进行一个改进，将 孩子结点 存储下来，并且需要记录下每个结点有几个孩子结点。
  也就是说，我们可以对每个结点定义成结构体，总共四个成员：数据域、孩子结点数量域、孩子结点数组。

2）源码详解

typedef struct  {
    DataType data;
    int childCount;     // (1)
    int childs[MAXN];   // (2)
}TreeNode; 

• $(1)$ childCount记录下当前这个结点有多少个孩子结点；
• $(2)$ childs[i]则代表第 $i$ 个孩子结点在Tree的结点列表nodes[]中的下标；

3）图片剖析

  同样是这样一棵树，[0]代表第 0 号结点，它的数据域为 $a$，其中 0 为数组下标；[1]代表第 1 号结点，它的数据域为 $b$，以此类推。

  得到的结构体数组如下：

下标	data	childCount	childs
0	$a$	$2$	$[1,2]$
1	$b$	$1$	$[3]$
2	$c$	$2$	$[4,5]$
3	$d$	$3$	$[6,7,8]$
4	$e$	$0$	$[]$
5	$f$	$0$	$[]$
6	$g$	$0$	$[]$
7	$h$	$0$	$[]$
8	$i$	$0$	$[]$

4）结构剖析

  这种存储结构中，通过结点获取 孩子结点 的均摊时间复杂度为 $O(1)$。但是，如果想要知道某个结点有的父结点是哪个，则必须遍历整棵树才行。
  所以，我们一般可以将 父亲表示法 和 孩子表示法 混用，这样，在知道某个结点的情况下，都能快速得到它的 父结点 和 子结点。
  但是这种表示法的空间时间复杂度为 $O(n^2)$，当 $n$ 较大时，并不是很友好。

3、左儿子右兄弟

1）存储方式

  对于任意一棵树，每个结点的 第一个孩子结点 如果存在就一定是唯一的，它的 右兄弟结点 如果存在也是唯一的。因此，对于每个结点，我们可以设置两个域，分别代表 第一个孩子结点 和 右兄弟结点。

2）源码详解

typedef struct  {
    DataType data;
    int left;     // (1)
    int right;    // (2)
二万字《算法和数据结构》三张动图，三十张彩图，C语言基础教学，之 二叉搜索树详解 (建议收藏)

 二万字《算法和数据结构》三张动图，三十张彩图，C语言基础教学，之 二叉搜索树详解 (建议收藏)
 《画解数据结构》C语言基础讲解，三张动图，三十张彩图，画解二叉搜索树 (建议收藏)
 《画解数据结构》C语言基础讲解，三张动图，三十张彩图，画解二叉搜索树 (建议收藏)
 ❤️《画解数据结构》两万字，十张动图，画解双端队列❤️(建议收藏)
 ❤️《画解数据结构》两万字，十张动图，画解双端队列❤️(建议收藏)