❤️《画解数据结构》两万字，十张动图，画解双端队列❤️(建议收藏)

Posted 2021-09-28 英雄哪里出来

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了❤️《画解数据结构》两万字，十张动图，画解双端队列❤️(建议收藏)相关的知识，希望对你有一定的参考价值。

您可能感兴趣的文章推荐 画解顺序表画解链表画解栈画解队列画解哈希表画解二叉树画解图画解排序

零、前言

「数据结构」 和 「算法」 是密不可分的，两者往往是「相辅相成」的存在，所以，在学习 「数据结构」 的过程中，不免会遇到各种「算法」。
到底是先学数据结构，还是先学算法，我认为不必纠结这个问题，一定是一起学的。
数据结构常用的操作一般为：「增」「删」「改」「查」。基本上所有的数据结构都是围绕这几个操作进行展开的。
那么这篇文章，作者将用 「十张动图」 来阐述一种 「两端插入」「两端弹出」 的数据结构

「双端队列」

🔥让天下没有难学的算法🔥
C语言免费动漫教程，和我一起打卡！ 🌞《光天化日学C语言》🌞
入门级C语言真题汇总 🧡《C语言入门100例》🧡
几张动图学会一种数据结构 🌳《画解数据结构》🌳
组团学习，抱团生长 🌌《算法入门指引》🌌
竞赛选手金典图文教程 💜《夜深人静写算法》💜
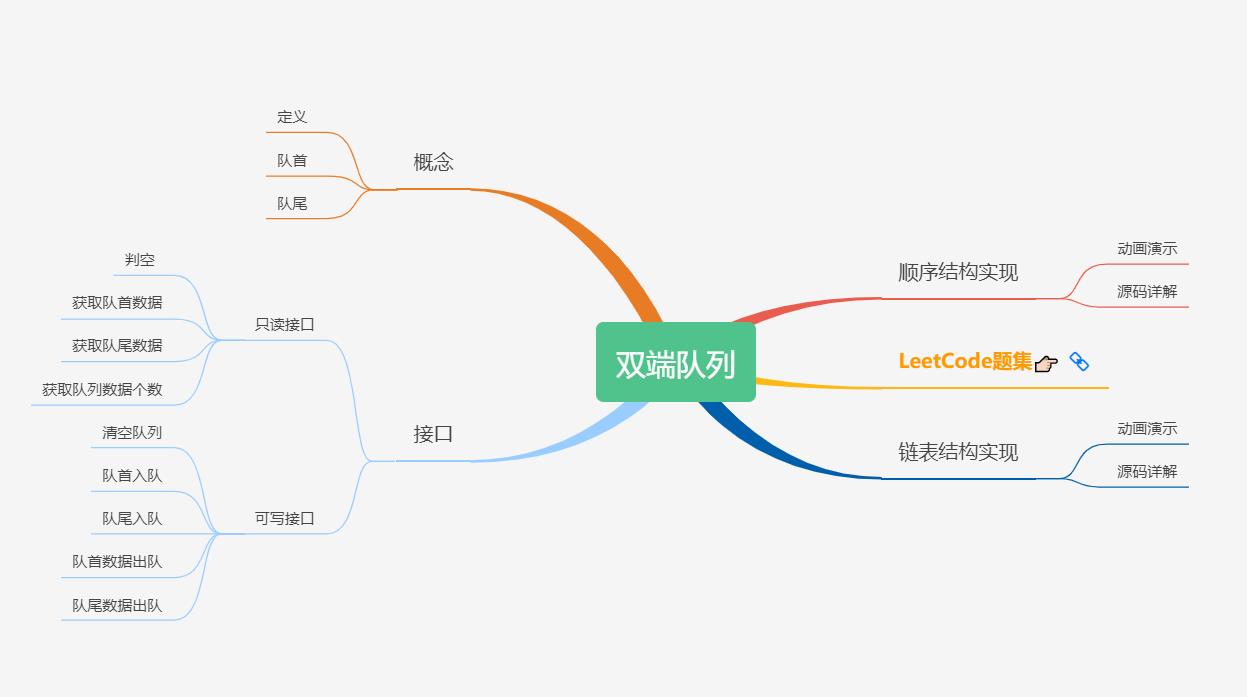
双端队列可以用 顺序表 实现，也可以用 双向链表 实现，浓缩为以下两张图：

看不懂没有关系，我会把它拆开来一个一个讲，首先来看一下今天要学习的内容目录。

一、概念

1、双端队列的定义

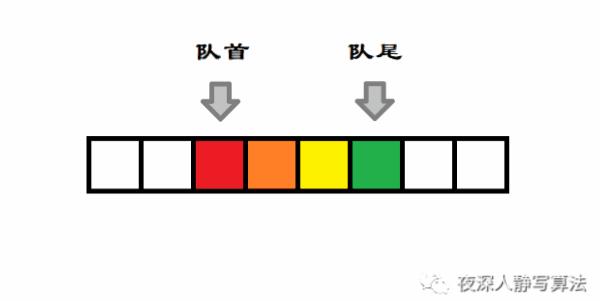
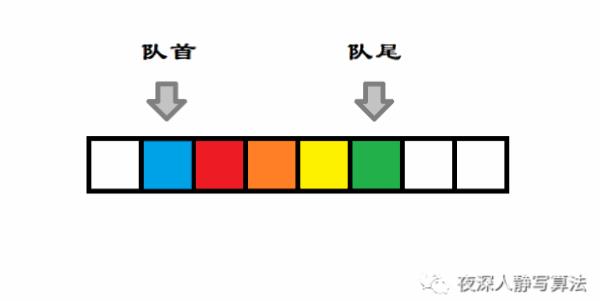
双端队列 是一种具有队列和栈的性质的数据结构，是我们常说的 deque（double-ended queue），是一种限定插入和删除操作在表的两端进行的线性表。这两端分别被称为队首和队尾。

1）模拟栈

双端队列 可以用来在一端进行插入和删除，从而实现栈的功能。如图所示，代表的是队首固定，队尾循环进行 插入和删除 操作，从而模拟栈的入栈和出栈的过程。

有关栈的更多内容，可以参考作者的另一篇文章：❤️《画解数据结构》九个动图，画解栈❤️。

2）模拟队列

双端队列 也可以用限定只在一端插入，另一删除，从而实现队列的功能。如图所示，代表的是队尾进行插入，队首进行插入，从而模拟 FIFO 队列的入队和出队的过程。

有关 FIFO队列的更多内容，可以参考作者的另一篇文章：❤️《画解数据结构》九张动图，画解队列❤️。

3）输出受限队列

还可以实现 输出受限 的双端队列，即一个端点允许 插入和删除，另一个端点只允许插入的双端队列。

4）输入受限队列

也可以实现 输入受限 的双端队列，即一个端点允许 插入和删除，另一个端点只允许删除的双端队列。这种结构，我们一般可以它来实现 单调队列。
有关 单调队列 相关内容，下周会在《夜深人静写算法》专栏进行更新。

2、队首

双端队列的一端被称为队首，如下图所示：

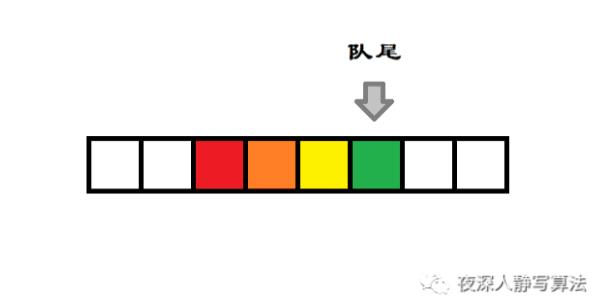
3、队尾

双端队列的另一端被称为队尾，如下图所示：

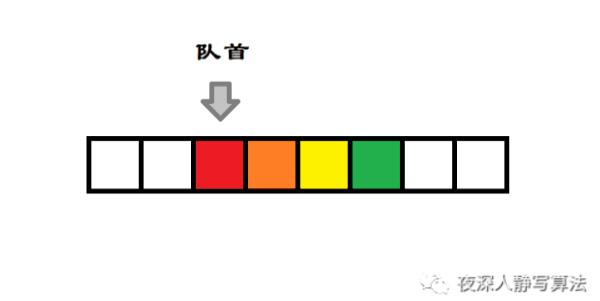
二、接口

1、可写接口

1）队首入队

队列的插入操作，叫做入队。
队首入队 就是将 数据元素 从队首进行插入的过程。如图所示，表示的是在队首插入一个蓝色数据的过程：

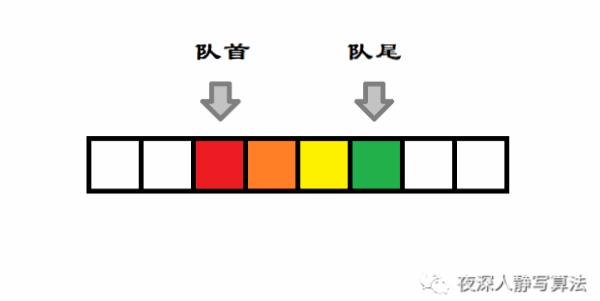
2）队尾入队

队尾入队 就是将 数据元素 从队尾进行插入的过程。如图所示，表示的是在队尾插入一个紫色数据的过程：

3）队首出队

队列的删除操作，叫做出队。
队首出队 是将队首元素进行删除的过程，如图所示，表示的是在队首删除一个蓝色数据的过程：

4）队尾出队

队尾出队 是将队尾元素进行删除的过程，如图所示，表示的是在队尾删除一个紫色数据的过程：

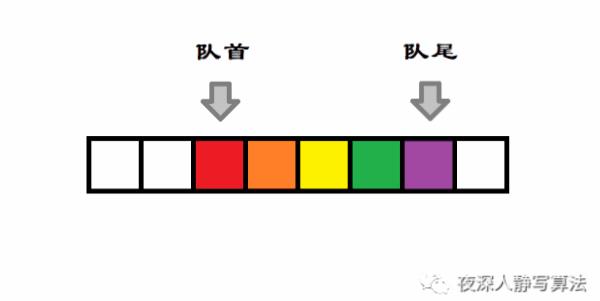
5）清空队列

队列的清空操作，就是一直出队，直到队列为空的过程，当队首和队尾正好错开一个位置时，就代表队尾为空了，如图所示，细心的读者会发现，队尾和队首错开了一个位置：

2、只读接口

1）获取队列元素个数

队列元素个数一般用一个额外变量存储，入队时加一，出队时减一。这样获取队列元素的时候就不需要遍历整个队列。通过 $O (1)$ 的时间复杂度获取队列元素个数。

2）判空

当队列元素个数为零时，就是一个空队，空队不允许出队操作。

3）获取队首元素

队首指针 指向的数据被称为 队首元素，可以通过 $O (1)$ 的时间复杂度来获取。

4）获取队尾元素

队尾指针 指向的数据被称为 队尾元素，可以通过 $O (1)$ 的时间复杂度来获取。

三、双端队列的顺序表实现

1、数据结构定义

对于顺序表，在 C语言中表现为数组，在进行 双端队列的定义 之前，我们需要考虑以下几点：
1）队列数据的存储方式，以及队列数据的数据类型；
2）队列的大小；
3）队首指针；
4）队尾指针；

我们可以定义一个 双端队列 的 结构体，C语言实现如下所示：

#define DataType int         // (1)
#define maxn 100005          // (2)

struct Queue {               // (3)
    DataType data[maxn<<1];  // (4)
    int head, tail;          // (5)
};

$(1)$ 用DataType这个宏定义来统一代表队列中数据的类型，这里将它定义为整型，根据需要可以定义成其它类型，例如浮点型、字符型、结构体等等；
$(2)$ maxn代表我们定义的队列的最大元素个数的一半，因为对于数组来说，不能有负数下标，所以初始情况是从数组的中心开始往两边进行插入删除，所以实际的数组长度为maxn的两倍；
$(3)$ Queue就是我们接下来会用到的 双端队列 的 结构体；
$(4)$ DataType data[maxn<<1]作为 队列元素 的存储方式，即数组，其中元素个数为maxn<<1，等价于maxn*2，数据类型为DataType，可以自行定制；
$(5)$ head即 队首指针，tail即 队尾指针，head - tail == 1代表空队；当队列非空时，data[head]代表了队首元素，data[tail]代表了队尾元素；

2、队首入队

1）动画演示

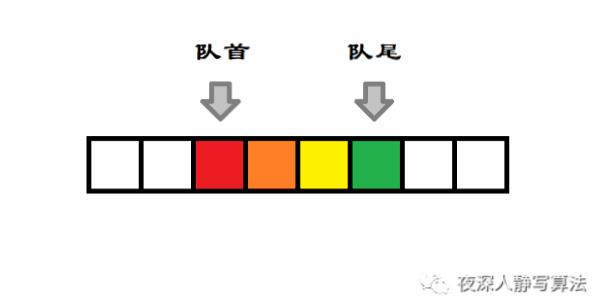
如图所示，蓝色元素 为新插入队首的数据，执行前，队首指针减一，然后在对应位置插入数据。具体来看下代码实现。

2）源码详解

队首入队 操作，只需要两行代码就能实现，代码实现如下：

void QueueEnqueueFront(struct Queue *que, DataType dt) {
    --que->head;                             // (1)
    que->data[ --que->head ] = dt;           // (2)
}

$(1)$ 队首指针左移一个位置（逻辑上是减一）；
$(2)$ 将需要插入的数据放到 队首指针 对应位置上即完成了入队操作。

注意，这个接口在调用前，需要保证 队首指针 大于零，否则就会使数组下标变负数，导致数组下标越界。

3、队尾入队

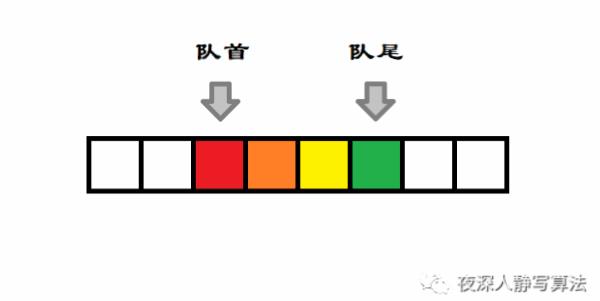
1）动画演示

如图所示，紫色元素 为新插入队尾的数据，执行前，队尾指针加一，然后在对应位置插入数据。具体来看下代码实现。

2）源码详解

队尾入队 操作，也只需要两行代码就能实现，代码实现如下：

void QueueEnqueueRear(struct Queue *que, DataType dt) {
    ++que->tail;                             // (1)
    que->data[que->tail] = dt;               // (2)
}

$(1)$ 队尾指针右移一个位置（逻辑上是加一）；
$(2)$ 将需要插入的数据放到 队尾指针 对应位置上即完成了入队操作。

注意，这个接口在调用前，需要保证 队尾指针 小于 maxn*2，否则就会导致数组下标越界。

4、队首出队

1）动画演示

如图所示，蓝色元素 为原先的 队首元素，执行出队操作以后，红色元素 成为当前的 队首元素，出队操作只是将 队首指针 加一。由于是顺序表实现，队首元素前面的那些元素已经变成无效的了，具体来看下代码实现。

2）源码详解

队首出队 操作，只需要简单的改变，将 队首指针 加一即可，原先的 队首元素 不需要理会，代码实现如下：

void QueueDequeueFront(struct Queue* que) {
    ++que->head;
}

5、队尾出队

1）动画演示

如图所示，紫色元素 为原先的 队尾元素，执行出队操作以后，绿色元素 成为当前的 队尾元素，出队操作只是将 队尾指针 减一。由于是顺序表实现，队尾元素 后面的那些元素已经变成无效的了，具体来看下代码实现。

2）源码详解

队尾出队 操作，只需要简单的改变，将 队尾指针 减一即可，原先的 队尾元素 不需要理会，代码实现如下：

void QueueDequeueRear(struct Queue* que) {
    --que->tail;
}

6、清空队列

对于顺序表来说，清空队列的操作只需要将 队首指针 置为 maxn，而 队尾指针 置为 队首指针 减一即可，数据不需要清理，下次继续入队的时候会将之前的内存重复利用。
这里需要注意的是，顺序表的实际最大长度为maxn的两倍，为了满足 双端队列 能够在两端都进行入队这个性质，所以才把初始位置设置在了顺序表的中点，也就是maxn的位置。
清空队列的操作，代码实现如下：

void QueueClear(struct Queue* que) {
    que->head = maxn;
    que->tail = que->head - 1;
}

7、只读接口

只读接口包含：获取队首元素、获取队尾元素、获取队列大小、队列的判空，实现如下：

DataType QueueGetFront(struct Queue* que) {
    return que->data[ que->head ];            	// (1)
}
DataType QueueGetRear(struct Queue* que) {
    return que->data[ que->tail ];              // (2)
}
int QueueGetSize(struct Queue* que) {
    return que->tail - que->head + 1;           // (3)
}
int QueueIsEmpty(struct Queue* que) {
    return !QueueGetSize(que);                  // (4)
}

$(1)$ que->head代表了 队首指针，即 队首下标，所以真正的 队首元素 是 que->data[ que->head ]；
$(2)$ que->tail代表了 队尾指针，即 队尾下标，所以真正的 队尾元素 是 que->data[ que->tail ]；
$(3)$ 当队列为空时，que->tail == que->head - 1。直观的感受下，入队会把 队首指针 和 队尾指针 的距离拉开，出队会把 队首指针 和 队尾指针 的距离拉近；所以，队列的元素个数就是两者差值加一。
$(4)$ 当 队列元素 个数为零时，队列为空。

8、双端队列的顺序表实现源码

双端队列的顺序表实现的源码如下：

/**************************** 顺序表 实现双端队列 ****************************/
#define DataType int
#define maxn 100005

struct Queue {
    DataType data[maxn<<1];
    int head, tail;
};

void QueueClear(struct Queue* que) {
    que->head = maxn;
    que->tail = que->head - 1;
}

void QueueEnqueueFront(struct Queue *que, DataType dt) {
    que->data[ --que->head ] = dt;
}
void QueueEnqueueRear(struct Queue *que, DataType dt) {
    que->data[ ++que->tail ] = dt;
}
void QueueDequeueFront(struct Queue* que) {
    ++que->head;
}
void QueueDequeueRear(struct Queue* que) {
    --que->tail;
}

DataType QueueGetFront(struct Queue* que) {
    return que->data[ que->head ];
}
DataType QueueGetRear(struct Queue* que) {
    return que->data[ que->tail ];
}
int QueueGetSize(struct Queue* que) {
    return que->tail - que->head + 1;
}
int QueueIsEmpty(struct Queue* que) {
    return !QueueGetSize(que);
}

/**************************** 顺序表 实现双端队列 ****************************/

四、双端队列的链表实现

1、数据结构定义

对于链表，在进行 双端队列的定义 之前，我们需要考虑以下几个点：
1）队列数据的存储方式，以及队列数据的数据类型；
2）队列的大小；
3）队首指针；
4）队尾指针；

我们可以定义一个 双端队列 的 结构体，C语言实现如下所示：

#define DataType int              // (1)
struct QueueNode;                 // (2)
struct QueueNode {                // (3)
    DataType data;
    struct QueueNode *prev;
    struct QueueNode *next;
};

struct Queue {
    struct QueueNode *head, *tail;// (4)
    int size;                     // (5)
};

$(1)$ 队列结点元素的 数据域，这里定义为整型；
$(2)$ struct QueueNode;是对 链表结点 的声明；
$(3)$ 定义链表结点，其中DataType data代表 数据域；struct QueueNode *prev代表 前驱指针域；struct QueueNode *next代表 后继指针域；注意，双端队列 需要用 双向链表 实现，单向链表 无法满足需求；
$(4)$ head作为 队首指针，tail作为 队尾指针；
$(5)$ 由于 求链表长度 的算法时间复杂度是 $O (n)$ 的，所以我们需要记录一个size来代表现在队列中有多少元素。每次入队时size自增，出队时size自减。这样在询问队列的大小的时候，就可以通过 $O (1)$ 的时间复杂度。

2、创建链表结点

在进行入队操作的时候，需要将数据转换成双向链表的结点，所以需要通过malloc分配结点的内存，实现如下：

struct QueueNode *QueueCreateNode(DataType dt) {
    struct QueueNode *vtx = (struct QueueNode *) malloc( sizeof(struct QueueNode));
    vtx->data = dt;                      // (1)
    vtx->next = vtx->prev = NULL;        // (2)
    return vtx;
}

$(1)$ 将传入参数作为 数据域；
$(2)$ 将 前驱指针 和 后继指针 都置为空，代表创建完毕后，这是一个孤立的双向链表结点；

3、入队操作

双端队列 的入队操作分为 队首入队 和 队尾入队，我们将两种实现通过一个统一的内部接口_QueueEnqueue来实现，并且用一个标记isFrontOrRear来表示是从队首进行入队的，还是从队尾进行入队的，C语言实现如下：

void _QueueEnqueue(struct Queue *que, DataType dt, int isFrontOrRear) {
    struct QueueNode *vtx = QueueCreateNode(dt);  // (1)
    if(que->size == 0) {
        que->head = que->tail = vtx;              // (2)
    }else {
        if(isFrontOrRear) {                       // (3)    
            vtx->next = que->head;                // (4)
            que->head->prev = vtx;
            que->head = vtx;                      // (5)
        }else {
            que->tail->next = vtx;                // (6)
            vtx->prev = que->tail;
            que->tail = vtx;                      // (7)
        }
    } 
    ++que->size;                                  // (8)
}

$(1)$ 创建一个 数据域 为dt的结点vtx；
$(2)$ 如果目前是一个空的双端队列，则将 队首指针 和 队尾指针 都指向vtx；
$(3)$ 如果非空，则需要考虑是 队首入队 还是 队尾入队。用传参isFrontOrRear进行判断。
$(4) - (5)$ 如果是 队首入队，则将vtx的后继指向队首，并且将vtx作为新的队首；
$(6) - (7) 以上是关于❤️《画解数据结构》两万字，十张动图，画解双端队列❤️(建议收藏)的主要内容，如果未能解决你的问题，请参考以下文章 ❤️《画解数据结构》七张动图，画解单调队列❤️(建议收藏) ❤️《画解数据结构》全网最全队列总结，九张动图搞懂队列 ❤️(文末有投票) 《画解数据结构》C语言基础讲解，三张动图，三十张彩图，画解二叉搜索树 (建议收藏) 《画解数据结构》C语言基础讲解，三张动图，三十张彩图，画解二叉搜索树 (建议收藏) ❤️《画解数据结构》全网最清晰哈希表入门，三张动图搞懂哈希 ❤️(建议收藏) 《画解数据结构》九张动图，画解队列$