print("\\n定义一级函数")
y1 = w1 * x  + b1
print("y1=", y1)

print("\\n定义二级函数")
y2 = w2 * y1 + b2
print("y2=", y2)

print("\\n(1)全过程自动链式求导")
y2.backward(retain_graph=True)
print("w1.grad=", w1.grad)
print("b1.grad=", b1.grad)
print("w2.grad=", w2.grad)
print("b2.grad=", b2.grad)

全局函数法：torch.autograd.grad(tensor, [w,b], retain_graph=True)

print("\\n(2)指定链自动链式求导")
dy2_dw1 = torch.autograd.grad(y2, [w1], retain_graph=True)[0]
dy2_db1 = torch.autograd.grad(y2, [b1], retain_graph=True)[0]
dy2_dw2 = torch.autograd.grad(y2, [w2], retain_graph=True)[0]
dy2_db2 = torch.autograd.grad(y2, [b2], retain_graph=True)[0]
print("dy2_dw1=", dy2_dw1)
print("dy2_db1=", dy2_db1)
print("dy2_dw2=", dy2_dw2)
print("dy2_db2=", dy2_db2)

（6）自动清除常量：grad.data.zero_()

Pytorch每次自动求导/求梯度时，会自动累加之前的计算结果，因此，需要提供一种机制，在需要的时候，自动复位导数。

xxx_tensor.grad.data.zero_()

第3章 autograd的子类：autograd.Variable类（变量）

autograd.Variable 是autograd中最核心的类。

它包装了一个Tensor，并且几乎支持所有在其上定义的操作。一旦完成了你的运算，你可以调用 .backward()来自动计算出所有的梯度。

Variable是对Tensor的一个封装，因此Tensor具备的操作，Variable都具备。

Variable还引入了三个额外的属性：

data：Variable变量用于存放变量本身的数值
grad：Variable变量用于存放变量针对某一个函数f的偏导数值.
grad_fn：计算梯度的函数

Tensor对Variable类型的指示

requires_grad=True

第4章 autograd的子类：autograd.Function函数类（运算）

PyTorch：定义新的 Autograd 函数 · Pytorch 中文文档

4.1 autograd.Function的直观理解

Function简单说就是对Variable的运算，如加减乘除，relu，pool等。
Pytorch是利用Variable与Function构了建计算图，一个表示运算（函数），一个表示数据（自变量或因变量）
Function（函数）不仅仅可以定义简单的函数，还可以定义复杂的自定义函数
Function（函数）的主要成员包含前向运算的函数forward和反向运算的backward函数。

Function应用也非常广泛，特别是需要定义复杂运算的时候。

4.2 理解autograd.Function重要的意义

（1）autograd.Function对于理解符合函数的正向传播非常有帮助，autograd.Function需要定义正向传播的函数

（2）autograd.Function对于理解符合函数的反向传播非常有帮助，autograd.Function需要定义反向传播的函数

4.3 autograd.Function定义的函数在符合函数中的位置

autograd.Function自定义的书序函数，是整个复合函数中的一个环节。

4.4 为什么要自定义 autograd.Function的数学函数

因为默认的函数求导时通过数值拟合来实现对任意函数的求导的，存在一定的误差。

为了提高特定函数的导函数的精度，如果知道了原函数的形态，可以通过解析的方式获取其导函数的形态，然后直接通过导函数，求函数的导数，这样就不需要通过默认的数值计算的方法，近似求导了。

如原函数：y(x) = x3^3 + x^2 + x + 1

其导数是非常清楚的：y'(x) = 3*x^2 + 2*x.

用导函数求得的导数的精度，肯定要比数值计算获得的导数的精度要高。

4.5 Function与Module的差异与应用场景

Function一般只定义一个操作，因为其无法保存参数，因此适用于激活函数、pooling等操作；

Module是保存了参数，因此适合于定义一层，如线性层，卷积层，也适用于定义一个网络。

Function需要定义三个方法：__init__, forward, backward（需要自己写求导公式）；

Module：只需定义__init__和forward，而backward的计算由自动求导机制构成。

可以不严谨的认为，Module是由一系列Function组成，因此其在forward的过程中，Function和Variable组成了计算图，在backward时，只需调用Function的backward就得到结果，因此Module不需要再定义backward。

Module不仅包括了Function，还包括了对应的参数，以及其他函数与变量，这是Function所不具备的。

4.6 Functon函数自动求导的基本原理

[数值计算-19]：万能的任意函数的数值求导数方法_文火冰糖（王文兵）的博客-CSDN博客

4.7 Functon的定义与成员函数

（1）操作“类”定义

class LegendrePolynomial3(torch.autograd.Function):
    def __init__:
        ###

    @staticmethod
    def forward(ctx, input):
        ##
     
    @staticmethod
    def backward(ctx, grad_output):
        ###

（2）__init__：初始化函数

该成员函数，用于对自定义的类进行初始化。

（3）foward (ctx, input）

ctx: pytorch定义的上下文管理器
input：复合函数的输入

def forward(ctx, input):
        """
        In the forward pass we receive a Tensor containing the input and return
        a Tensor containing the output. ctx is a context object that can be used
        to stash information for backward computation. You can cache arbitrary
        objects for use in the backward pass using the ctx.save_for_backward method.
        """
        ctx.save_for_backward(input)
        return 0.5 * (5 * input ** 3 - 3 * input)

f(x) = 1/2 * (5 * x^3 - 3 * x)

（3）backward(ctx，grad_out)

ctx: pytorch定义的上下文管理器
grad_out：该函数的导函数的输出

 @staticmethod
    def backward(ctx, grad_output):
        """
        In the backward pass we receive a Tensor containing the gradient of the loss
        with respect to the output, and we need to compute the gradient of the loss
        with respect to the input.
        """
        input, = ctx.saved_tensors
        return grad_output * 1.5 * (5 * input ** 2 - 1)

f(x)的导函数为 f '(x) = 1/2 * (5 * x^3 - 3 * x)

4.8 如何使用自定义的function进行前向计算

# 普通的神经元的串联（复用）
y_pred1 = w2 * (w1 * x + b1)  + b2



# 生成一个自定义的操作对象P3（对输入数据预处理）
P3 = LegendrePolynomial3.apply

# 使用p3对第一级神经元的输出进行预处理，处理后的数据，作为第2级神经元的输入。
y_preprocessed = P2(w1 * x + b1)
y_pred2 = w2 * y_preprocess + b2

备注：

（1）对于y_pred1：

前一级的输出（w1*wx + b1) 直接作为后一级的输入x，这是一种未对输入数据进行预加工的串联模型。

（2）对于y_pred2

y_pred2与y_pred1类似，是两级处理的串联，但y_pred2对上一级y_pred1的输出的数据，并没有直接作为自身的输入，而是对它进行了预加工。

P3=LegendrePolynomial3.apply的作用是生成一个新的预加工对象P3.

P3拥有自定义的类LegendrePolynomial3的前向运算函数forward(ctx, input)

P3拥有自定义的类LegendrePolynomial3的后向运算函数backward(ctx, grad_output):

4.9 如何使用自定义的function进行反向求导（梯度）计算

（1）定义损失函数

#定义平方和损失函数
loss = (y_pred - y).pow(2).sum()

（2）自动链式求导

   # Use autograd to compute the backward pass.
    loss.backward()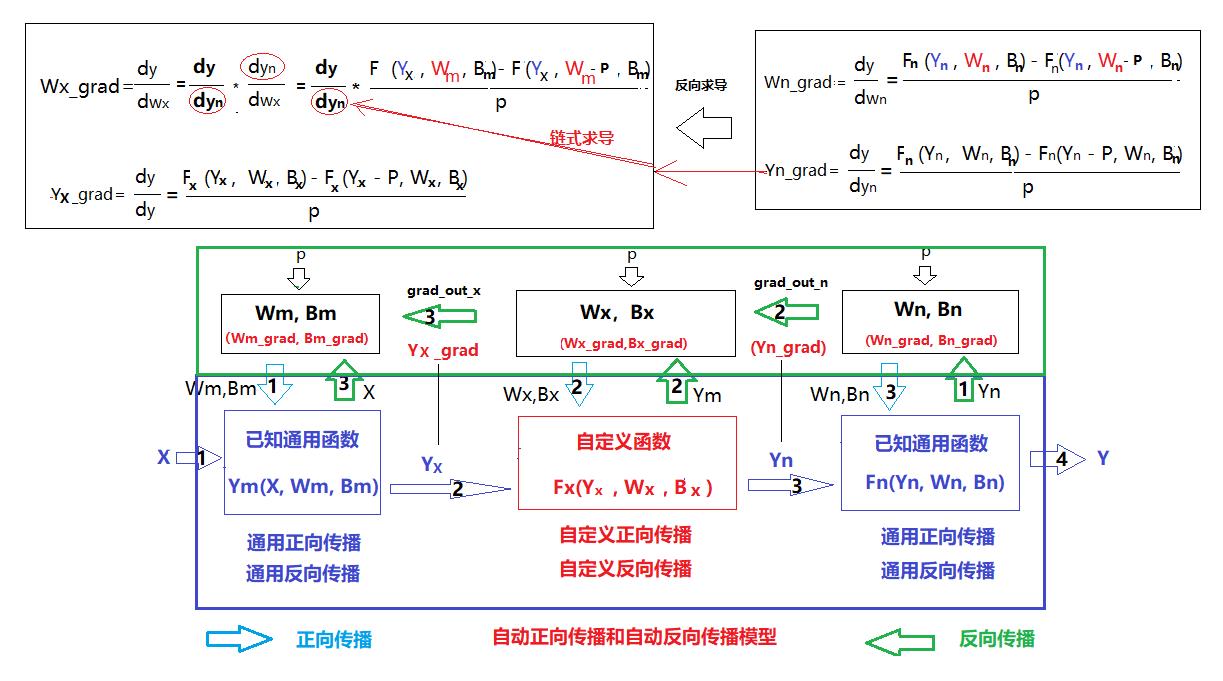

loss.backward()的作用是进行自动链式求导。

（1）非自定义函数的求导

在链式求导的过程中，若果遇到的是非自定义函数的处理环节，则使用系统默认的求导方式求导，包括使用已知函数的导函数的方式求导和使用通用的数值计算的方法求导。

（2）自定义函数的求导

在链式求导的过程中，遇到自定函数的处理环节是，会自动调用自定义的backward(ctx, grad_output)函数进行求导。

第5章代码示例与解读

5.1 自定义操作函数：继承autograd.Function


class LegendrePolynomial3(torch.autograd.Function):
    """
    We can implement our own custom autograd Functions by subclassing
    torch.autograd.Function and implementing the forward and backward passes
    which operate on Tensors.
    """

    @staticmethod
    def forward(ctx, input):
        """
        In the forward pass we receive a Tensor containing the input and return
        a Tensor containing the output. ctx is a context object that can be used
        to stash information for backward computation. You can cache arbitrary
        objects for use in the backward pass using the ctx.save_for_backward method.
        """
        ctx.save_for_backward(input)
        return 0.5 * (5 * input ** 3 - 3 * input)

    @staticmethod
    def backward(ctx, grad_output):
        """
        In the backward pass we receive a Tensor containing the gradient of the loss
        with respect to the output, and we need to compute the gradient of the loss
        with respect to the input.
        """
        input, = ctx.saved_tensors
        return grad_output * 1.5 * (5 * input ** 2 - 1)

5.2 准备样本数据

#准备样本数据
dtype = torch.float
device = torch.device("cpu")
# device = torch.device("cuda:0")  # Uncomment this to run on GPU

# Create Tensors to hold input and outputs.
# By default, requires_grad=False, which indicates that we do not need to
# compute gradients with respect to these Tensors during the backward pass.
x = torch.linspace(-math.pi, math.pi, 2000, device=device, dtype=dtype)
y = torch.sin(x)  #输入样本是[-Pi, +Pi]之间的正弦函数

5.3 构建拟合函数

#构建前向预测函数
# Create random Tensors for weights. For this example, we need
# 4 weights: y = a + b * P3(c + d * x), these weights need to be initialized
# not too far from the correct result to ensure convergence.
# Setting requires_grad=True indicates that we want to compute gradients with
# respect to these Tensors during the backward pass.
b2 = torch.full((), 0.0, device=device, dtype=dtype, requires_grad=True)
w2 = torch.full((), -1.0, device=device, dtype=dtype, requires_grad=True)
b1 = torch.full((), 0.0, device=device, dtype=dtype, requires_grad=True)
w1 = torch.full((), 0.3, device=device, dtype=dtype, requires_grad=True)

P3 = LegendrePolynomial3.apply
y_pred = b2 + w2 * P3(b1 + w1 * x)

5.3 构建loss函数

# Compute and print loss
size = x.size()[0]
loss = ((y_pred - y).pow(2).sum())/size
print("initial loss=", loss)

initial loss= tensor(0.2310, grad_fn=<DivBackward0>)

5.4 训练模型：梯度下降法迭代式

learning_rate = 5e-6

for t in range(4000):
    # To apply our Function, we use Function.apply method. We alias this as 'P3'.
    P3 = LegendrePolynomial3.apply

    # Forward pass: compute predicted y using operations; we compute
    # P3 using our custom autograd operation.
    
    # 用下列前向计算函数拟合正弦函数
    y_pred = b2 + w2 * P3(b1 + w1 * x)

    # Compute and print loss
    size = x.size()[0]
    loss = ((y_pred - y).pow(2).sum())/size
    
    if t % 1000 == 999:
        print(t,":", loss.item())

    # Use autograd to compute the backward pass.
    loss.backward()

    # Update weights using gradient descent
    # 梯度下降法求函数loss函数的最小值
    with torch.no_grad():
        b2 -= learning_rate * b2.grad
        w2 -= learning_rate * w2.grad
        b1 -= learning_rate * b1.grad
        w1 -= learning_rate * w1.grad

        # Manually zero the gradients after updating weights
        b2.grad = None
        w2.grad = None
        b1.grad = None
        w1.grad = None

print(f'Result: y = {b2.item()} + {w2.item()} * P3({b1.item()} + {w1.item()} x)')

999 : 0.19282658398151398
1999 : 0.1754167526960373
2999 : 0.1662026047706604
3999 : 0.16083794832229614
Result: y = 3.075185245338119e-11 + -1.0044142007827759 * P3(-1.2000908600207083e-10 + 0.2654314637184143 x)

5.6 拟合效果评估：图形法

print(b1)
print(b1.data)
print(b1.item())

multiple = 2.2
y_sample_data = y
y_pred_data = b2.item() + w2.item() * P3 (b1.item() + w1.item() * x) 
y_pred_multiple = y_pred_data * multiple

#样本图形
plt.scatter(x, y_sample_data, color="black", linewidth = 1)

#拟合图形
plt.scatter(x, y_pred_data, color="red" , linewidth = 1)

#修正的图形
plt.scatter(x, y_pred_multiple, color="blue" , linewidth = 1)

tensor(-1.2001e-10, requires_grad=True)
tensor(-1.2001e-10)
-1.2000908600207083e-10

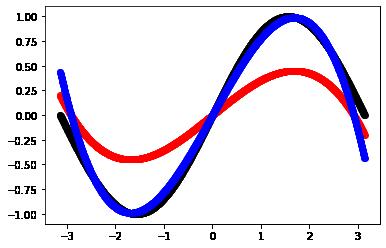
从上图可以看出，拟合图形（红色）与样本数据（黑色）是相似的，但幅度上相差较大。

因此通过修正，在拟合图形的基础之上，在乘以一个倍数2（蓝色），这时候，修正后的图形与样本数据的图形，基本重合。

作者主页(文火冰糖的硅基工坊)：文火冰糖（王文兵）的博客_文火冰糖的硅基工坊_CSDN博客

本文网址：https://blog.csdn.net/HiWangWenBing/article/details/120300699

以上是关于[Pytorch系列-22]：Pytorch基础 - Autograd库 Autograd.Function与反向自动求导机制的主要内容，如果未能解决你的问题，请参考以下文章

[Pytorch系列-18]：Pytorch基础 - 张量的范数

[Pytorch系列-20]：Pytorch基础 - Varialbe变量的手工求导和自动链式求导

[Pytorch系列-21]：Pytorch基础 - 反向链式求导的全过程拆解

[Pytorch系列-19]：Pytorch基础 - Variable变量的使用方法与 Tensor变量的比较

[PyTroch系列-16]：PyTorch基础 - 张量的操作 - 变形

[PyTroch系列-13]：PyTorch基础 - 张量的操作 - 筛选过滤

[Pytorch系列-22]：Pytorch基础 - Autograd库 Autograd.Function与反向自动求导机制

第1章 Autograd库简介

1.1 Autograd库的简介与作用

1.2 Autograd库在Pytorch架构中的位置

第2章 Autograd对张量tensor的改进

2.1 相关参考：

2.2 核心要点