[Pytorch系列-20]：Pytorch基础 - Varialbe变量的手工求导和自动链式求导

Posted 文火冰糖的硅基工坊

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了[Pytorch系列-20]：Pytorch基础 - Varialbe变量的手工求导和自动链式求导相关的知识，希望对你有一定的参考价值。

作者主页(文火冰糖的硅基工坊)：文火冰糖（王文兵）的博客_文火冰糖的硅基工坊_CSDN博客

本文网址：https://blog.csdn.net/HiWangWenBing/article/details/120251332

目录

第1章 Varialbe变量基础

第2章 Tensor自变量的手工求导

2.1 一元函数在某点(x_i)处对一元Tensor变量求导

2.2  一元函数在序列(x_1，x_2......x_n)处对一元tensor变量求导

第3章 Varialbe因变量的手工求导

3.1 一元函数y对一元Varaible变量x在某一点处的一阶导数

3.2 一元函数y对一元Varaible变量x在一连串点处的一阶导数序列

3.3 二元函数对一元Varaible变量在某一点处的一阶偏导数

3.3 二元函数对一元Varaible变量在一连串点处的一阶偏导数序列

第4章 Varialbe变量的自动求导

4.1 一元函数y对一元Varaible变量在某一点(x)处的一阶导数

4.2 多元函数y对一元Varaible变量在某一点(x1, x2, .....xn) 处的一阶偏导数

第5章 Varialbe变量的自动求导的几个注意点

5.1 默认情况下梯度自动累加，不是当前值

5.2 梯度清零的方法：variable.grad.data.zero_()

5.3 pytorch动态图带来的问题

第6章 自动求导的应用：梯度下降迭代

6.1 梯度下降迭代

6.2 自动求导、梯度下降迭代的关键点

6.3 可视化迭代过程

6.4 可视化原函数

第1章 Varialbe变量基础

[Pytorch系列-19]：Pytorch基础 - Variable变量的使用方法与 Tensor变量的比较_文火冰糖（王文兵）的博客-CSDN博客

第2章 Tensor自变量的手工求导

这种方式，必须预先人工根据导数的公式，写出原函数的导函数。

并通过导函数计算导数，这种方法，虽然说是求导，实际上就是普通的函数计算。、

这种情形下，其实并不一定需要Varialbe变量，普通的Tensor变量也是可以的。

2.1 一元函数在某点(x_i)处对一元Tensor变量求导

# 一元函数在某点(x_i)处对一元Tensor变量求导
# Tensor张量与手工求导函数
print("自变量：张量tensor       => 自变量值")
x_tensor = torch.Tensor([0])  
print("x_tensor =", x_tensor)

print("\\n因变量：一元原函数     => 原函数值")
y_tensor = x_tensor ** 2 + 1  
print("y_tensor =",y_tensor)

print("\\n因变量：手工求导前     => 导函数值 ")
print("x_tensor.grad =", x_tensor.grad)

print("\\n对原函数的所有变量分别手工求偏导(通过手工定义的导函数)")
y_tensor_grad_x  = 2 * x_tensor

print("\\n因变量：手工求导后     => 导函数值")
print("y_tensor_grad_x =", y_tensor_grad_x)
print("x_tensor.grad =", x_tensor.grad)
自变量：张量tensor       => 自变量值
x_tensor = tensor([0.])

因变量：一元原函数     => 原函数值
y_tensor = tensor([1.])

因变量：手工求导前     => 导函数值 
x_tensor.grad = None

对原函数的所有变量分别手工求偏导(通过手工定义的导函数)

因变量：手工求导后     => 导函数值
y_tensor_grad_x = tensor([0.])
x_tensor.grad = None

这里可以看出：

  • Varialbe是一种tensor
  • tensor也是一种Varialbe
  • 普通的tensor，梯度是None

2.2  一元函数在序列(x_1，x_2......x_n)处对一元tensor变量求导

# 一元函数在n个点序列(x_1，x_2......x_n)处对一元Tensor变量求导
# Tensor张量与手工求导函数
print("自变量：张量tensor       => 自变量值序列")
x_tensor = torch.Tensor([-3, -2,-1,0, 1, 2, 3])  
print("x_tensor =", x_tensor)

print("\\n因变量：一元原函数     => 原函数值序列")
y_tensor = x_tensor ** 2 + 1  
print("y_tensor =",y_tensor)

print("\\n因变量：手工求导前     => 导函数值序列 ")
print("x_tensor.grad =", x_tensor.grad)

print("\\n对原函数的所有变量分别手工求偏导(通过手工定义的导函数)")
y_tensor_grad_x  = 2 * x_tensor  #一次可以获得多个点处的导数值

print("\\n因变量：手工求导后     => 导函数值序列 ")
print("y_tensor_grad_x =", y_tensor_grad_x)
print("x_tensor.grad =", x_tensor.grad)
自变量：张量tensor       => 自变量值序列
x_tensor = tensor([-3., -2., -1.,  0.,  1.,  2.,  3.])

因变量：一元原函数     => 原函数值序列
y_tensor = tensor([10.,  5.,  2.,  1.,  2.,  5., 10.])

因变量：手工求导前     => 导函数值序列 
x_tensor.grad = None

对原函数的所有变量分别手工求偏导(通过手工定义的导函数)

因变量：手工求导后     => 导函数值序列 
y_tensor_grad_x = tensor([-6., -4., -2.,  0.,  2.,  4.,  6.])
x_tensor.grad = None

第3章 Varialbe因变量的手工求导

在这一章节，演示Varialbe变量的手工求导，看看Varialbe变量与Tensor变量的相同地方。

从总体上看，在手工求导方面，其实是相同的，就是不同的tensor运算。

3.1 一元函数y对一元Varaible变量x在某一点处的一阶导数

# Tensor张量与手工求导函数
# 一元函数在n个点(x)处对一元Variable变量求导
print("自变量：张量tensor       => 自变量值")
x_variable = Variable(torch.Tensor([1]), requires_grad = True)
print("x_variable =", x_variable)

print("\\n因变量：一元原函数     => 函数值")
y_variable = x_variable ** 2 + 1  
print("y_variable =", y_variable)

print("\\n因变量：手工求导前     => 导函数值")
print("x_variable.grad =", x_variable.grad)

print("\\n对原函数的所有变量分别手工求偏导(通过手工定义的导函数)")
y_variable_grad_x  = 2 * x_variable

print("\\n因变量：手工求导后     => 导函数值 ")
print("y_variable_grad_x =", y_variable_grad_x)
print("x_variable.grad =", x_variable.grad)
自变量：张量tensor       => 自变量值
x_variable = tensor([1.], requires_grad=True)

因变量：一元原函数     => 函数值
y_variable = tensor([2.], grad_fn=<AddBackward0>)

因变量：手工求导前     => 导函数值
x_variable.grad = None

对原函数的所有变量分别手工求偏导(通过手工定义的导函数)

因变量：手工求导后     => 导函数值 
y_variable_grad_x = tensor([2.], grad_fn=<MulBackward0>)
x_variable.grad = None

备注：

  • 没有自动求导时，即使Varialbe变量，其梯度也是为None
  • Varialbe变量本身是tensor

3.2 一元函数y对一元Varaible变量x在一连串点处的一阶导数序列

# Tensor张量与手工求导函数
# 一元函数在n个点序列(x_1，x_2......x_n)处对一元Variable变量求导
print("自变量：张量tensor       => 自变量值")
x_variable = Variable(torch.Tensor([-3, -2,-1,0, 1, 2, 3]), requires_grad = True)
print("x_variable =", x_variable)

print("\\n因变量：一元原函数     => 函数值")
y_variable = x_variable ** 2 + 1  
print("y_variable =", y_variable)

print("\\n因变量：手工求导前     => 导函数值")
print("x_variable.grad =", x_variable.grad)

print("\\n对原函数的所有变量分别手工求偏导(通过手工定义的导函数)")
y_variable_grad_x  = 2 * x_variable

print("\\n因变量：手工求导后     => 导函数值 ")
print("y_variable_grad_x =", y_variable_grad_x)
print("x_variable.grad =", x_variable.grad)
自变量：张量tensor       => 自变量值
x_variable = tensor([-3., -2., -1.,  0.,  1.,  2.,  3.], requires_grad=True)

因变量：一元原函数     => 函数值
y_variable = tensor([10.,  5.,  2.,  1.,  2.,  5., 10.], grad_fn=<AddBackward0>)

因变量：手工求导前     => 导函数值
x_variable.grad = None

对原函数的所有变量分别手工求偏导(通过手工定义的导函数)

因变量：手工求导后     => 导函数值 
y_variable_grad_x = tensor([-6., -4., -2.,  0.,  2.,  4.,  6.], grad_fn=<MulBackward0>)
x_variable.grad = None

备注：

  • 自动求导前，x_variable变量的梯度为None

3.3 二元函数对一元Varaible变量在某一点处的一阶偏导数

二元函数的求导，实际上是对每个变量分别求偏导。

# Variable变量与手工导
# 二元函数在点(x1，x2)处对一元Variable变量分别求偏导
print("自变量：张量tensor => 自变量值")
x_variable1 =  Variable(torch.Tensor([0]), requires_grad = True)
x_variable2 =  Variable(torch.Tensor([0]), requires_grad = True)
print("x_variable1 =", x_variable1)
print("x_variable2 =", x_variable2)

print("\\n因变量：二元源函数     => 函数值")
y_variable = x_variable1**2 + x_variable2**2 + 1
print("y_variable =", y_variable)

print("\\n因变量：手动求导前     => 导数值")
print("x_variable1.grad =", x_variable1.grad)
print("x_variable2.grad =", x_variable2.grad)


print("\\n对原函数的所有变量分别手工求偏导")
y_variable_grad_x1  = 2 * x_variable1
y_variable_grad_x2  = 2 * x_variable2

print("\\n因变量：手动求导后     => 导数值 ")
#获取导数值
print("对x1变量求偏导")
print("x_variable1 =", x_variable1) 
print("x_variable1.grad =", x_variable1.grad)  #获取x1处的偏导数
print("y_variable_grad_x1 =", y_variable_grad_x1)

print("\\n对x2变量求偏导")
print("x_variable2 =", x_variable2) 
print("x_variable2.grad =", x_variable2.grad)  #获取x1处的偏导数
print("y_variable_grad_x2 =", y_variable_grad_x2)
自变量：张量tensor => 自变量值
x_variable1 = tensor([0.], requires_grad=True)
x_variable2 = tensor([0.], requires_grad=True)

因变量：二元源函数     => 函数值
y_variable = tensor([1.], grad_fn=<AddBackward0>)

因变量：手动求导前     => 导数值
x_variable1.grad = None
x_variable2.grad = None

对原函数的所有变量分别手工求偏导

因变量：手动求导后     => 导数值 
对x1变量求偏导
x_variable1 = tensor([0.], requires_grad=True)
x_variable1.grad = None
y_variable_grad_x1 = tensor([0.], grad_fn=<MulBackward0>)

对x2变量求偏导
x_variable2 = tensor([0.], requires_grad=True)
x_variable2.grad = None
y_variable_grad_x2 = tensor([0.], grad_fn=<MulBackward0>)

3.3 二元函数对一元Varaible变量在一连串点处的一阶偏导数序列

一连串点处的求导，是对每个点进行单独求导。

# Variable变量与手工求导
# 二元函数在点序列[(x1_1，x2_1),(x1_2，x2_2),...(x1_n，x2_n)] 处对一元Variable变量分别求偏导
print("自变量：张量tensor => 自变量值")
x_variable1 =  Variable(torch.Tensor([-3, -2,-1,0, 1, 2, 3]), requires_grad = True)
x_variable2 =  Variable(torch.Tensor([-3, -2,-1,0, 1, 2, 3]), requires_grad = True)
print("x_variable1 =", x_variable1)
print("x_variable2 =", x_variable2)

print("\\n因变量：二元源函数     => 函数值")
y_variable = x_variable1**2 + x_variable2**2 + 1
print("y_variable =", y_variable)

print("\\n因变量：手动求导前     => 导数值")
print("x_variable1.grad =", x_variable1.grad)
print("x_variable2.grad =", x_variable2.grad)

print("\\n对原函数的所有变量分别手工求偏导(通过手工定义的导函数)")
y_variable_grad_x1  = 2 * x_variable1
y_variable_grad_x2  = 2 * x_variable2

print("\\n因变量：手动求导后     => 导数值 ")
#获取导数值
print("对x1变量求偏导")
print("x_variable1 =", x_variable1) 
print("x_variable1.grad =", x_variable1.grad)  #获取x1处的偏导数
print("y_variable_grad_x1 =", y_variable_grad_x1)

print("\\n对x2变量求偏导")
print("x_variable2 =", x_variable2) 
print("x_variable2.grad =", x_variable2.grad)  #获取x1处的偏导数
print("y_variable_grad_x2 =", y_variable_grad_x2)
自变量：张量tensor => 自变量值
x_variable1 = tensor([-3., -2., -1.,  0.,  1.,  2.,  3.], requires_grad=True)
x_variable2 = tensor([-3., -2., -1.,  0.,  1.,  2.,  3.], requires_grad=True)

因变量：二元源函数     => 函数值
y_variable = tensor([19.,  9.,  3.,  1.,  3.,  9., 19.], grad_fn=<AddBackward0>)

因变量：手动求导前     => 导数值
x_variable1.grad = None
x_variable2.grad = None

对原函数的所有变量分别手工求偏导(通过手工定义的导函数)

因变量：手动求导后     => 导数值 
对x1变量求偏导
x_variable1 = tensor([-3., -2., -1.,  0.,  1.,  2.,  3.], requires_grad=True)
x_variable1.grad = None
y_variable_grad_x1 = tensor([-6., -4., -2.,  0.,  2.,  4.,  6.], grad_fn=<MulBackward0>)

对x2变量求偏导
x_variable2 = tensor([-3., -2., -1.,  0.,  1.,  2.,  3.], requires_grad=True)
x_variable2.grad = None
y_variable_grad_x2 = tensor([-6., -4., -2.,  0.,  2.,  4.,  6.], grad_fn=<MulBackward0>)

第4章 Varialbe变量的自动求导

在引入Variable后，在forward时，自动生成了计算图，

backward就不需要我们手工计算了，pytorch将根据计算图自动计算梯度。

自动求导不支持一连串数值点的的自动求导，只支持单个节点。

但自动求导支持多元函数（多元参数）的自动一次性求所有参数的偏导。

4.1 一元函数y对一元Varaible变量在某一点(x)处的一阶导数

# Variable变量与自动求导
# 自动求导只能在某一个点,如一元点(x）处一次自动求导，不能对一个点序列进行多次的连续自动求导
print("自变量：张量tensor => 自变量值")
x_variable =  Variable(torch.Tensor([0]), requires_grad = True)
print("x_variable =", x_variable)

print("\\n因变量：一元原函数     => 函数值")
y_variable = x_variable ** 2 + 1
print("y_variable =", y_variable)

print("\\n因变量：自动求导前     => 导数值")
print("x_variable =", x_variable)
print("x_variable.grad =", x_variable.grad)

print("\\n对原函数的所有变量分别自动求偏导（通过系统提供的backward（）成员函数）")
y_variable.backward()  

print("\\n因变量：自动求导后     => 导数值 ")
print("x_variable =", x_variable)
print("x_variable.grad =", x_variable.grad)
自变量：张量tensor => 自变量值
x_variable = tensor([0.], requires_grad=True)

因变量：一元原函数     => 函数值
y_variable = tensor([1.], grad_fn=<AddBackward0>)

因变量：自动求导前     => 导数值
x_variable = tensor([0.], requires_grad=True)
x_variable.grad = None

对原函数的所有变量分别自动求偏导（通过系统提供的backward（）成员函数）

因变量：自动求导后     => 导数值 
x_variable = tensor([0.], requires_grad=True)
x_variable.grad = tensor([0.])

备注：

  • 通过y_variable.backward()  实现对函数y_variable的所有自变量一次性求偏导数
  • backward() 反向链式求导，具体求导算法由深度学习框架实现。
  • backward() 是任意函数变量y的成员函数，这里是y_variable = x_variable ** 2 + 1
  • backward() 执行后，会自动更新函数对应的所有自变量（x1,x2....xn)在当前值处的偏导数，并存放到自变量对应的grad成员中，这里是x_variable

4.2 多元函数y对一元Varaible变量在某一点(x1, x2, .....xn) 处的一阶偏导数

# 二元函数自动求导
# 自动求导只能在某一个点,如二元点(x1,x2）处一次自动求导，不能对一个点序列进行多次的连续自动求导
print("自变量：张量tensor => 自变量值")
x_variable1 =  Variable(torch.Tensor([-1]), requires_grad = True)
x_variable2 =  Variable(torch.Tensor([1]), requires_grad = True)
print("x_variable1 =", x_variable1)
print("x_variable2 =", x_variable2)

print("\\n因变量：二元原函数     => 函数值")
y_variable = x_variable1**2 +  x_variable2**2 + 1
print("y_variable =", y_variable)

print("\\n因变量：自动求导前     => 导数值")
print("x_variable1 =", x_variable1)
print("x_variable1.grad =", x_variable1.grad)
print("x_variable2 =", x_variable2)
print("x_variable2.grad =", x_variable2.grad)

print("\\n对原函数的所有变量分别自动求偏导（通过系统提供的backward（）成员函数）")
y_variable.backward()  

print("\\n因变量：自动求导后     => 导数值 ")
#获取导数值
print("x_variable1 =", x_variable1)
print("x_variable1.grad =", x_variable1.grad)
print("x_variable2 =", x_variable2)
print("x_variable2.grad =", x_variable2.grad)

自变量：张量tensor => 自变量值
x_variable1 = tensor([-1.], requires_grad=True)
x_variable2 = tensor([1.], requires_grad=True)

因变量：二元原函数     => 函数值
y_variable = tensor([3.], grad_fn=<AddBackward0>)

因变量：自动求导前     => 导数值
x_variable1 = tensor([-1.], requires_grad=True)
x_variable1.grad = None
x_variable2 = tensor([1.], requires_grad=True)
x_variable2.grad = None

对原函数的所有变量分别自动求偏导（通过系统提供的backward（）成员函数）

因变量：自动求导后     => 导数值 
x_variable1 = tensor([-1.], requires_grad=True)
x_variable1.grad = tensor([-2.])
x_variable2 = tensor([1.], requires_grad=True)
x_variable2.grad = tensor([2.])
  • 通过y_variable.backward()  实现对函数y_variable的所有自变量一次性求偏导数
  • backward() 反向链式求导，具体求导算法由深度学习框架实现。
  • backward() 是任意函数变量y的成员函数，这里是y_variable = x_variable ** 2 + 1
  • backward() 执行后，会自动更新函数对应的所有自变量（x1,x2....xn)在当前值处的偏导数，并存放到自变量对应的grad成员中，这里是x_variable1、x_variable2

第5章 Varialbe变量的自动求导的几个注意点

5.1 默认情况下梯度自动累加，不是当前值

# 梯度自动累加：即使点的位置没有变化，每次计算出来的梯度值是累加的。
x_variable =  Variable(torch.Tensor([1]), requires_grad = True)
print("x_variable =", x_variable)
print("x_variable.grad = ", x_variable.grad)
y_variable = x_variable ** 2 + 1
print("y_variable=", y_variable)

# 自动求导
count = 5
while(count):
    print("\\n", count)

    y_variable.backward(retain_graph=True)  
    
    y_variable = x_variable ** 2 + 1
    print("x_variable=", x_variable)
    print("y_variable=", y_variable)
    print("x_variable.grad = ", x_variable.grad)
    
    count = count - 1
x_variable = tensor([1.], requires_grad=True)
x_variable.grad =  None
y_variable= tensor([2.], grad_fn=<AddBackward0>)

 5
x_variable= tensor([1.], requires_grad=True)
y_variable= tensor([2.], grad_fn=<AddBackward0>)
x_variable.grad =  tensor([2.])

 4
x_variable= tensor([1.], requires_grad=True)
y_variable= tensor([2.], grad_fn=<AddBackward0>)
x_variable.grad =  tensor([4.])

 3
x_variable= tensor([1.], requires_grad=True)
y_variable= tensor([2.], grad_fn=<AddBackward0>)
x_variable.grad =  tensor([6.])

 2
x_variable= tensor([1.], requires_grad=True)
y_variable= tensor([2.], grad_fn=<AddBackward0>)
x_variable.grad =  tensor([8.])

 1
x_variable= tensor([1.], requires_grad=True)
y_variable= tensor([2.], grad_fn=<AddBackward0>)
x_variable.grad =  tensor([10.])

备注：

  • 在上述5次迭代中，自变量y_variable的数值并没有变，x_variable = 1
  • 在上述5次迭代中，自变量y_variable的数值并没有变，y_variable = 2
  • 点（1,2）处的导数理论值为：2
  • (x=1, y=2)点处的导数（梯度），在每次自动求导后，点（1,2）处的导数却一直在变化：2-》4-》6-》8-》10
  • 原因：这是由于自动求导后，梯度是自动、默认累加的。因为点（1,2）并没有变化，其理论的导数值为2，因此自动累加的步长为2. 起始值为2,。

5.2 梯度清零的方法：variable.grad.data.zero_()

# 梯度自动累加 
x_variable =  Variable(torch.Tensor([1]), requires_grad = True)
print("x_variable =", x_variable)
print("x_variable.grad = ", x_variable.grad)
y_variable = x_variable ** 2 + 1
print("y_variable=", y_variable)

# 自动求导
count = 5
while(count):
    print("\\n", count)

    y_variable.backward(retain_graph=True)  
    
    y_variable = x_variable ** 2 + 1
    print("x_variable=", x_variable)
    print("y_variable=", y_variable)
    print("x_variable.grad = ", x_variable.grad)
    
    count = count - 1
    
    #清除x_variable以前的梯度值
    x_variable.grad.data.zero_()
x_variable = tensor([1.], requires_grad=True)
x_variable.grad =  None
y_variable= tensor([2.], grad_fn=<AddBackward0>)

 5
x_variable= tensor([1.], requires_grad=True)
y_variable= tensor([2.], grad_fn=<AddBackward0>)
x_variable.grad =  tensor([2.])

 4
x_variable= tensor([1.], requires_grad=True)
y_variable= tensor([2.], grad_fn=<AddBackward0>)
x_variable.grad =  tensor([2.])

 3
x_variable= tensor([1.], requires_grad=True)
y_variable= tensor([2.], grad_fn=<AddBackward0>)
x_variable.grad =  tensor([2.])

 2
x_variable= tensor([1.], requires_grad=True)
y_variable= tensor([2.], grad_fn=<AddBackward0>)
x_variable.grad =  tensor([2.])

 1
x_variable= tensor([1.], requires_grad=True)
y_variable= tensor([2.], grad_fn=<AddBackward0>)
x_variable.grad =  tensor([2.])

备注：

  • 梯度清零后，在点的坐标值没有变化的情况下，每次自动求导后得到的梯度值是一致的，不变化的。

5.3 pytorch动态图带来的问题

上图中，y_variable.backward(retain_graph=True) 中的retain_graph=True作用是是？

设置静态图！

y_variable.backward(retain_graph=True)  的作用是设置y_variable的数据流图为静态，因为默认情况下Pytorch是动态图，每次运算完后，自动释放y_variable，如果不设置导致下次计算梯度时，导致y_variable未定义。

解决上述问题的方法有两个

（1）y_variable.backward(retain_graph=True)

（2）每次迭代时，重选定义计算图：y_variable = x_variable ** 2 + 1

如下图所示：

# 梯度自动累加 
x_variable =  Variable(torch.Tensor([1]), requires_grad = True)
print("x_variable =", x_variable)
print("x_variable.grad = ", x_variable.grad)
y_variable = x_variable ** 2 + 1
print("y_variable=", y_variable)

# 自动求导
count = 5
while(count):
    print("\\n", count)

    y_variable = x_variable ** 2 + 1
    y_variable.backward()  
    
    y_variable = x_variable ** 2 + 1
    print("x_variable=", x_variable)
    print("y_variable=", y_variable)
    print("x_variable.grad = ", x_variable.grad)
    
    count = count - 1
    
    #清除x_variable以前的梯度值
    x_variable.grad.data.zero_()

第6章 自动求导的应用：梯度下降迭代

6.1 梯度下降迭代

print("定义迭代的自变量参数以及初始值")
x1_variable =  Variable(torch.Tensor([2]), requires_grad = True)
x2_variable =  Variable(torch.Tensor([2]), requires_grad = True)
print("x1_variable =", x1_variable)
print("x2_variable =", x2_variable)

# 定义原函数
def loss_fun(x1, x2):
    y = x1**2 + x2**2 + 1
    return (y)

# 获取y初始值
y_variable = loss_fun (x1_variable, x2_variable)
print("y_variable   =", y_variable)

#定义学习率
learnning_rate = 0.1

#定义迭代次数
iterations = 30

#定义存放迭代过程数据的列表
x1_data = []
x2_data = []
y_data  = []

# 保存初始值：需转换成numpy，便于matlab可视化
x1_data.append(x1_variable.data.numpy())
x2_data.append(x2_variable.data.numpy())
y_data.append(y_variable.data.numpy())
print("\\n初始点：", x1_data[0], x2_data[0], y_data[0])


while(iterations):    
    # 对任意函数在当前位置求导数
    y_variable.backward()
    
    # 梯度下降迭代
    x1_variable.data = x1_variable.data - learnning_rate * x1_variable.grad
    x2_variable.data = x2_variable.data - learnning_rate * x2_variable.grad
    
    #计算当前最新的y值
    y_variable = loss_fun (x1_variable, x2_variable)
    
    #保存数据
    x1_data.append(x1_variable.data.numpy())
    x2_data.append(x2_variable.data.numpy())
    y_data.append(y_variable.data.numpy())
    
    #下次迭代做准备
    iterations = iterations -1
    x1_variable.grad.data.zero_()
    x2_variable.grad.data.zero_()
    
print("\\n迭代后的数据:")
print("x1_variable =", x1_variable.data.numpy())
print("x2_variable =", x2_variable.data.numpy())
print("y_variable   =", y_variable.data.numpy())

定义迭代的自变量参数以及初始值
x1_variable = tensor([2.], requires_grad=True)
x2_variable = tensor([2.], requires_grad=True)
y_variable   = tensor([9.], grad_fn=<AddBackward0>)

初始点： [2.] [2.] [9.]

迭代后的数据:
x1_variable = [0.00247588]
x2_variable = [0.00247588]
y_variable   = [1.0000123]

备注：

（1） 函数 y = x1**2 + x2**2 + 1

  • 其理论极小值为1
  • 位于（x1=0, x2=0）处。

（2）自动求导，梯度下降过程

  • 起始点坐标（x=2, y=2)
  • 学习率=0.1
  • 迭代次数=30
  • 迭代后坐标:  x1=0.00247588,  x2_variable=0.00247588
  • 迭代后的最小值：y_variable = 1.0000123

6.2 自动求导、梯度下降迭代的关键点

  • 每次迭代后要复位每个变量的梯度：

    x1_variable.grad.data.zero_()
    x2_variable.grad.data.zero_()

  • 迭代时，设置数据流图为静态图： y_variable.backward(retain_graph=True)  或 重选定义数据流图：y_variable = loss_fun (x1_variable, x2_variable)

在上述代码中，由于每次需要重选计算y的值，采用了第二种方案，重选定义数据流图。

6.3 可视化迭代过程

fig = plt.figure()
ax1 = plt.axes(projection='3d')        #使用matplotlib.pyplot创建坐标系
ax1.scatter3D(x1_data, x2_data, y_data, cmap='Blues')  #绘制三维散点图
plt.show()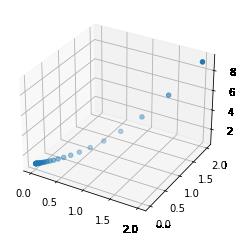

6.4 可视化原函数

# 可视化原函数的图形
x1_sample = np.arange(-10, 10, 1)
x2_sample = np.arange(-10, 10, 1)    #X,Y的范围

x1_grid, x2_grid = np.meshgrid(x1_sample,x2_sample)      #空间的点序列转换成网格点

y_grid = loss_fun(x1_grid,x2_grid)                 #生成z轴的网格数据

figure = plt.figure()
ax1 = plt.axes(projection='3d')             #创建三维坐标系

ax1.plot_surface(x1_grid, x2_grid, y_grid ,rstride=1,cstride=1,cmap='rainbow')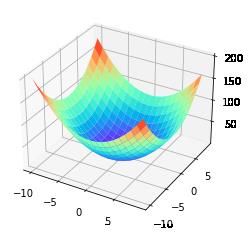

作者主页(文火冰糖的硅基工坊)：文火冰糖（王文兵）的博客_文火冰糖的硅基工坊_CSDN博客

本文网址：https://blog.csdn.net/HiWangWenBing/article/details/120251332

以上是关于[Pytorch系列-20]：Pytorch基础 - Varialbe变量的手工求导和自动链式求导的主要内容，如果未能解决你的问题，请参考以下文章

[Pytorch系列-18]：Pytorch基础 - 张量的范数

[Pytorch系列-22]：Pytorch基础 - Autograd库 Autograd.Function与反向自动求导机制

[Pytorch系列-21]：Pytorch基础 - 反向链式求导的全过程拆解

[Pytorch系列-19]：Pytorch基础 - Variable变量的使用方法与 Tensor变量的比较

[PyTroch系列-16]：PyTorch基础 - 张量的操作 - 变形

[PyTroch系列-13]：PyTorch基础 - 张量的操作 - 筛选过滤