机器学习笔记:梯度消失
Posted UQI-LIUWJ
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了机器学习笔记:梯度消失相关的知识,希望对你有一定的参考价值。
1 梯度消失
1.1 直观理解
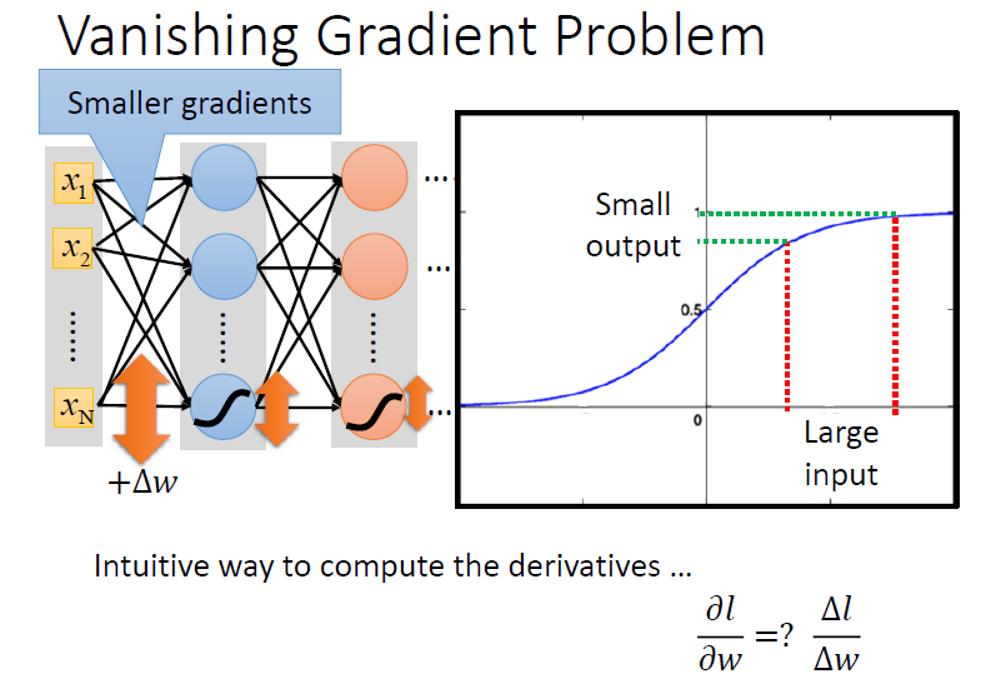
以sigmoid激活函数为例,如果我们使用sigmoid作为激活函数的话,很大的一个input的变化,经过了sigmoid之后的output变化会小很多。
这样经过很多层sigmoid之后,最后的输出变化会很小很小。
那么进行反向传播的时候,最后的损失函数传递到约远离输出的地方,值越小,那这些远离输出地方的参数更新得也就越慢
1.2 从反向传播的式子理解
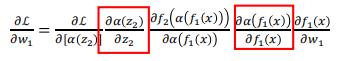
红框框住的是激活函数的导数,tanh和sigmoid的导数均小于1,这会导致训练深模型的时候出问题。
1.2.1 SVD分解
李宏毅线性代数笔记13:SVD分解_UQI-LIUWJ的博客-CSDN博客
令A表示激活函数,那么Ax就是经过激活函数之后的x
我们需要比较||Ax||和||x||
根据SVD,我们有: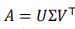 其中U和V是正交矩阵,奇异值σ1>σ2>...>σn>0
其中U和V是正交矩阵,奇异值σ1>σ2>...>σn>0
在李宏毅线性代数11: 正交(Orthogonality)_UQI-LIUWJ的博客-CSDN博客 中,我们说过,正交矩阵是norm-preserving的,所以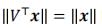
我们令||x||=c,假设A是满秩的,我们有:
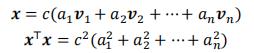 (正交基的线性组合)
(正交基的线性组合)
而 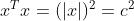
所以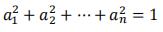
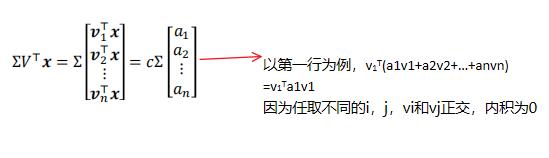
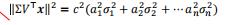
而我们之前有了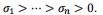 和
和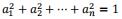
所以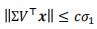 ,即
,即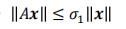
等号成立当且仅当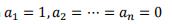 ,即
,即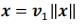
如果我们有很多个最大奇异值小于1的矩阵,那么最终的乘积会很小很小 ,这就导致了梯度消失
而tanh和sigmoid正满足这一特征,所以最终会导致梯度下降
2 几种梯度消失的解决方法
- 不同的激活函数,使得梯度=1
- 使用类似于Adam这样的优化函数,自适应地放缩梯度
- RNN中的LSTM等
3 梯度爆炸
在前面,我们有: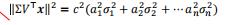
所以从另一个角度讲,也有 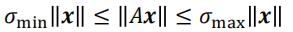
如果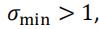 那么多个A相乘得到的结果将会很大很大,这就导致了梯度爆炸
那么多个A相乘得到的结果将会很大很大,这就导致了梯度爆炸
以上是关于机器学习笔记:梯度消失的主要内容,如果未能解决你的问题,请参考以下文章
ng机器学习视频笔记(十五) ——大数据机器学习(随机梯度下降与map reduce)
神经网络和深度学习笔记 - 第五章 深度神经网络学习过程中的梯度消失问题
