因果推断笔记——自整理因果推断理论解读
Posted 悟乙己
tags:
篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了因果推断笔记——自整理因果推断理论解读相关的知识，希望对你有一定的参考价值。
之前有整理过一篇：因果推断笔记—— 相关理论：Rubin Potential、Pearl、倾向性得分、与机器学习异同（二）
不过，那时候刚刚开始学，只能慢慢理解，所以这边通过一轮的学习再次整理一下手里的笔记。
文章目录
- 1 因果推断能做些啥
- 2 Causal Inference识别过程
- 3 Estimation的茫茫多方法
- 3.1 几种Estimation的套路
- 3.2 随机试验 (RCTs)
- 3.3 重加权方法之一：倾向得分 Propensity score and IPW(逆倾向加权)
- 3.4 重加权方法二：混杂因子平衡
- 3.5 匹配方法：很常见
- 3.6 Double Machine Learning (DML) / 回归
- 3.7 「元学习方法」（Meta-learning methods）
- 3.8 Doubly Robust Methods - DRM
- 3.9 工具变量(IV)
- 3.10 构造特殊对照组方法一：双重差分 - difference-in-difference -DID
- 3.12 构造特殊对照组方法二：合成控制SCM——Synthetic Control Method
- 3.13 断点回归模型
1 因果推断能做些啥
1.1 因果推断三个层次
《Theoretical Impediments to Machine Learning With Seven Sparks from the Causal Revolution》这篇论文说到了因果推断的三层。
原论文：
http://arxiv.org/abs/1801.04016
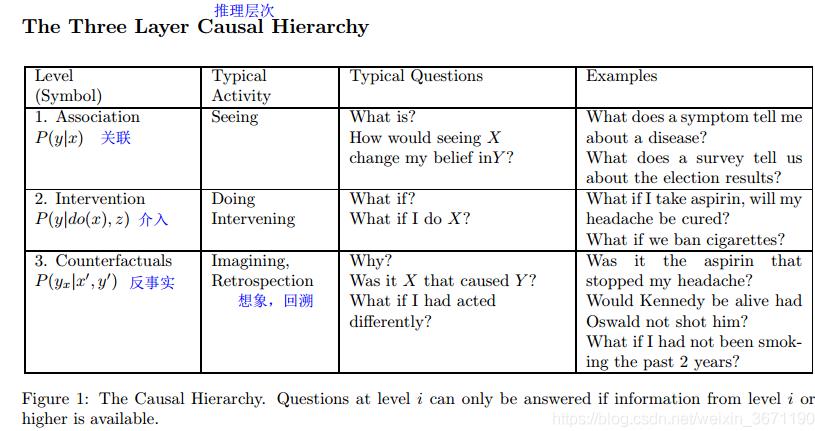
- 第一层是关联：纯粹的统计关系，X条件下Y会怎么样，也就是现在机器学习中常用的方式，尽可能通过深层次的网络去拟合X和Y的关系
观察一个购买牙膏的顾客，那么他/她购买牙线的可能性更大;这种关联可以使用条件期望直接从观察到的数据推断得出 - 第二层是干预：新的冲击下，两者的关联关系 ；这个层次的一个典型问题是：如果我们将价格翻倍会怎样？这些问题无法单独从销售数据中得到解答，因为它们涉及客户响应新的定价的行为的变化。
- 第三层是反事实推断：相当于对结果来考虑原因，相当于如果我们希望Y变化，那么我们需要对X做出什么样的改变？（下面贴原文，其实蛮费解的。。）
个人观点：因果推断可以补充机器学习方法过程中没有解释清楚的问题，一般ML都是解释X-> Y，但是没有说明白 Y-> X。
本节参考：
1.2 从因果效应开始说
1.2.1 TE/ATE/ATT/ATC/CATE 各类处理效应
因果推断就是推测某个试验(treatment)针对某个结果(outcome)的效应(effect)，所有的核心都是围绕：
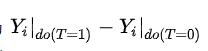
某些干预do(T=1)发生前、后的差异，这样就可以发现干预的重要性。
针对某个人的因果效应，称为ITE (Individual treatment effect)。
Fundamental Problem(Counterfactual)导致个体效应ITE无法识别，所以计算总体平均水平ATE：
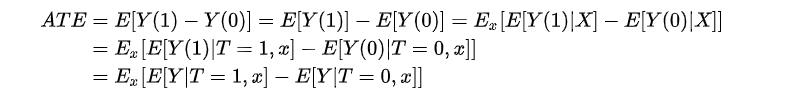
但是为了得到一致且无偏估计ATE (consistent & unbiased)那么就需要保证三个假定。
当然这里还有几种延伸效应：
在「干预组/实验组」层面，干预效果被称为「干预组的平均干预效果」（Average Treatment Effect on the Treated group, ATT），定义为：
类似地，对照组的平均干预效果被称为 「ATC」。
简单理解就是按某些规律进行分组之后的ATE，也就是“条件平均处理效应”(Conditional Average Treatment Effect，CATE)
一种异质处理效应的研究方法是将研究数据进行分组 (如按照男、女性别，或者区域进行划分) ，比较平均处理效果在子组内的效应差异。
每个子组的平均处理效应被称为“条件平均处理效应”(Conditional Average Treatment Effect，CATE) ，也就是说，每个子组的平均处理效应被称为条件平均处理效应，以子组内的分类方式为条件。
1.2.2 三个假定之 最难实现：无混淆性（Unconfoundedness ）
这里表达这个假定的名词有蛮多，一开始还一脸懵，怎么关于ATE的假定这么多，后面才发现每个假定都有N种外号：叫可忽略假设（Ignorability），也可以是CIA假定
也就是干预T 要与 outcome Y独立，基本不可能。。
所以可能看到后面很多的方法都是围绕这个，Identification阶段，后门调整、前门调整、RCT随机实验等。
还有经济学里的内生性问题，也是不满足该假定的。
CIA假定大多会引起两种问题：
- 「伪效应」（spurious effect）
- 选择偏差（selection bias），混杂因子会影响单元的干预选择，从而导致选择偏差的出现
举个例子，吃药（T） -> 头疼（Y），这里[年龄]就是一个混杂因子（W）：
- 伪效应，不同年纪吃药的剂量不一样，年轻还可以不吃（W -> T），年纪大了说不定本来就有头疼的毛病（W -> Y），那么这里如果计算ATE的话，这个ATE就不是单纯 吃药影响的，还夹带私活（W的存在）
- 选择偏差，在一些实验论证、计算因果效应CATE时候，会看到采集到头疼的样本，都是年纪大的，那么自然结果就因为年龄这个混杂因子W产生了偏差。
所以，针对选择偏差：
- 一般纯随机实验RCT就可以很好解决问题；
- Matching的方法是帮你找到最合适的实验-对照样本，不至于有偏
- 分层方法，也称为「子分类」（subclassification）或「区组」（blocking），是混杂因子调整的代表性方法。分层方法的核心思想是将整个组划分为同质性的亚组（区组）来调整干预组与对照组之间的偏差。
1.2.3 三个假定之二：正值假设（Positivity）
正值假设表示为公式即：
如果对于某些X的值，干预分配是确定的，则对于这些值来说，至少有一项干预所导致的结果是无法被观测的，这样我们也就无法去估计干预的因果效应。在上面的例子中，假定有两种干预：
药物 A 和药物 B，如果年龄大于 60 岁的患者总是给予药物 A，则我们就无法（也没有意义）去研究药物 B 在这些患者上的干预效果。
所以这里需要知道的是，一些实验干预，一定要有实验样本；
而且干预、混杂因子越多，所需的样本也越多
（至少多少样本 才是合适的，这个还要看具体情况而定）
另外：Unconfoundedness 和 Positivity看起来是相互制约的tradeoff的假设
1.2.4 三个假定之三：一致性假设（Consistency）
也可以叫：「稳定单元干预值假设」（Stable Unit Treatment Value Assumption, SUTVA）。
任意单元的潜在结果都不会因其他单元的干预发生改变而改变，且对于每个单元，其所接受的每种干预不存在不同的形式或版本，不会导致不同的潜在结果。
简单举个例子，T为是否养猫，Y为是否开心，不希望养了一只加菲T=1, 结果Y=1；养了一只美短T=1, 结果Y=0。说明T定义不好，这常在设计实验时容易出错。也叫No multiple version of Treatment
本节参考：
1.3 数据类型：实验数据 、 观测数据
来看一个腾讯看点分享的【2-1观测数据因果推断应用-启动重置体验分析】文章中，比较明确的将实验、观测数据进行拆分，并在各自数据状态下，适用不同的方法。
那么也就是说，如果有实验数据那就更科学，如果没有那就需要造实验参考组 或者 直接使用观测数据的方法。
2 Causal Inference识别过程
2.1 causal 的过程：Identification + Estimation
主要有两个步骤：
- Identification：我们感兴趣的是Causal Estimand (如ATE)，但是没法直接计算（因为我们只能计算统计量），需要转化为statistical Estimand (统计量)，这个过程叫Identification
- Estimation：根据statistical Estimand，利用data进行估计的数值，这个过程叫Estimation
那么这里Identification其实就是检验 + 确定这些个变量（T,X,W,Y）之间关系的过程，Identification过程再解释一下就是，修复假定，让ATE可以无偏估计的过程，这里需要确定的
E
（
Y
(
1
)
−
Y
(
0
)
）
E（Y(1) - Y(0)）
E（Y(1)−Y(0)）最终公式的过程，比如：
- 如果是RCT，随机实验的公式就是：
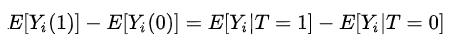
- 如果有混杂因子就需要后门调整、前门调整，也就是需要：
- 如果有混杂因子需要前门调整，就需要：
确认完成之后才是Estimation估计的过程，也就是，上面是把消除偏差的公式确认好之后，如何用数字计算的过程。
两个步骤整体就是在做：确认ATE无偏性下的公式（Identification），然后用数据计算出具体的数字（Estimation）
2.2 识别因果模式（Identification）的几种方式
为了得到无偏的ATE，在修复CIA、消除混淆因子影响过程中，比较重要的就是确认(W,T,Y)变量之间的关系，因为有些变量蛮难人为判定是否有因果关系的可能性，或者是混淆因子，以下是比较重要鉴定关系的方法：
- backdoor adjustment
- frontdoor adjustment
- Pearl’s do-calculus，之前介绍backdoor、frontdoor adjustment都是很直观直接可以从causal graph中判断identifiable。同时也存在以上两种方法不能Identity的情况。这里我们介绍一个complete 方法，只要是identifiable的都可以通过do-calculus识别
（具体前门准则、后门准则可参考之前的笔记：因果推断笔记—— 相关理论：Rubin Potential、Pearl、倾向性得分、与机器学习异同（二））
3 Estimation的茫茫多方法
这边单独成章，因为Estimation就是因果推断的核心，茫茫多的方法都是可以解决，而且解决方式各有千秋。
3.1 几种Estimation的套路
3.1.1 potential outcome model （虚拟事实模型 ）
potential outcome model （虚拟事实模型 ），也叫做Rubin Causal Model（RCM），希望估计出每个unit或者整体平均意义下的potential outcome，进而得到干预效果treatment effect(eg. ITE/ATE).
所以准确地估计出potential outcome是该框架的关键，由于混杂因子confounder的存在，观察到的数据不用直接用来近似potential outcome，需要有进一步的处理。
核心思想：寻找合适的对照组
3.1.2 因果图 causal graph model
有向图描述变量之间的因果关系。通过计算因果图中的条件分布，获得变量之间的因果关系。有向图指导我们使用这些条件分布来消除估计偏差，其核心也是估计检验分布、消除其他变量带来的偏差。
3.1.3 两个框架之间的联系
目的都是为了计算存在混淆变量时，干预变量时对结果的影响，都需要对因果关系作假设，以及控制带来偏差的变量；
不同点在于：
Rubin框架估计的因果效应主要是干预前后的期望差值
而Pearl框架下，我们估计的是干预前后的分布差异
Rubin框架解决的问题是因果效应的估计和统计推断
Pearl框架更偏向于因果关系的识别。
3.2 随机试验 (RCTs)
从CIA假设出发，因为有选择偏差，随机试验可以非常好的修复这一问题。
随机试验特点如下：
- 试验完全由随机决定 （T无causal parents）
- 此时treatment组和control组是可比的，因为其他因素在两个组分布均匀
- 此时可以通过条件期望计算因果效应
- 存在其他未观测confounding时，只要进行随机试验，就可以计算因果效应
Identification过程，如果是RCT，随机实验的公式就是：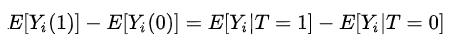
是否需要设定实验组、对照组，需要；
数据类型：横截面、时序、面板都行？？
当然，RCT很难实现，那么之后的【3.5 匹配的方法】可以非常好的，从观测数据中找到有价值的，实验组、对照组，然后继续进行实验。
3.3 重加权方法之一：倾向得分 Propensity score and IPW(逆倾向加权)
3.3.1 普通倾向得分 Propensity score
这里可以承接PSM
也是为了解决CIA假定，主要是打断X-> T的关系，就是CIA假定后面带来的选择偏差，同时，如果检测出有后门路径，那么IPW就是一个好办法，克服的主要方式就是逆倾向加权Inverse Probability Weighting (IPW)
其为每个样本分配一个权重r：
Identification过程 + estimation过程，就是：
计算过程，需要：
- 先构建
X->T的模型,e(x)
- 然后将e(x)带入
X->Y的模型中作为权重加权
研究表明，无论在大规模样本还是小规模样本中，倾向评分都能够平衡协变量所带来的选择偏差。
我们可以进一步将倾向评分与匹配、分层、回归等方法相结合，以消除协变量的影响。
当然，这里倾向得分还可以继续升级，普通的倾向得分主要问题有两个：
- IPW 估计器的正确性高度依赖于倾向评分估计的正确性，倾向评分的轻微错误会导致 ATE 的较大偏差
- IPW 估计器的另一个缺陷是当估计的倾向评分较小时，估计器可能会不稳定，如果任意一项干预分配的可能性较小，则用于估计倾向评分的逻辑回归模型可能会在尾部附近不稳定，从而导致 IPW 估计器的不稳定。
3.3.2 解决问题一：「双重稳健估计器」（DR） —— 加强 IPW（AIPW）
解决问题一：
- IPW 估计器的正确性高度依赖于倾向评分估计的正确性，倾向评分的轻微错误会导致 ATE 的较大偏差
为了解决这一问题，研究人员提出了「双重稳健估计器」（DR），也被称为加强 IPW（AIPW）。DR 估计器将倾向评分加权与结果回归相结合，可以保证即使部分评分或回归不正确（不能同时不正确），估计器仍具有鲁棒性。DR 估计器的具体公式如下：
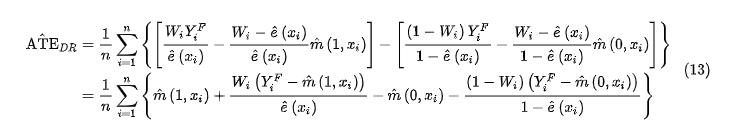只要倾向评分或模型能够正确地解释结果中混杂因子与变量之间的关系，DR 估计器就可以给出稳定且无偏的结果。
3.3.3 解决问题一：「协变量平衡倾向评分」（CBPS）
解决问题一：
- IPW 估计器的正确性高度依赖于倾向评分估计的正确性，倾向评分的轻微错误会导致 ATE 的较大偏差
另一种改善 IPW 估计器的方法是提升倾向评分估计的正确性。在 IPW 估计器中，倾向评分同时作为干预概率与协变量的平衡分数而出现，为了利用倾向评分的这一双重特性，研究人员提出了「协变量平衡倾向评分」（CBPS），其通过解决如下问题来估计倾向评分：
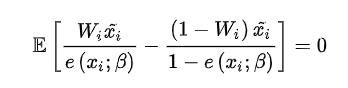
CBPS 的一种扩展是「协变量平衡广义倾向评分」（CBGPS），其能够处理「连续值」的干预。对于连续值干预来说，很难直接去最小化干预组与对照组之间的协变量分布距离，CBGPS 通过弱化平衡分数的定义来解决这一问题。基于原始定义，干预分配需要条件独立于背景变量，而 CBGPS 则选择将加权后的干预分配与协变量之间的相关性最小化（相比独立来说要求变低了）。
3.3.4 解决问题二：「修整」（trimming）与「重叠权重」（overlap weight）
解决问题二：
- IPW 估计器的另一个缺陷是当估计的倾向评分较小时，估计器可能会不稳定，如果任意一项干预分配的可能性较小，则用于估计倾向评分的逻辑回归模型可能会在尾部附近不稳定，从而导致 IPW 估计器的不稳定。
为了解决这个问题，一种常规的解决方式是进行「修整」（trimming），其可以视为一种正则化方法，通过预定义一个阈值，去除倾向评分小于该阈值的样本来提升估计器的稳定性。
然而，研究表明这种方法对修整的阈值高度敏感，同时较小的倾向评分结合修整的过程可能会导致 IPW 估计器中出现不同的非高斯渐近分布。
基于这些问题，研究者们提出了一种「双向鲁棒性 IPW 估计」方法（two-way robustness IPW estimation)，这种方法将子采样与基于局部多项式回归的修整偏差校正器相结合，对于较小的倾向评分与较大的修整阈值均具有鲁棒性。
另一种克服小倾向评分下 IPW 不稳定性的替代性方案是重新设计样本权重，研究者们提出了一种「重叠权重」（overlap weight），其中每个单元的权重与该单元分配到对立组的概率成比例。重叠权重的大小被限制在区间 [公式] 以内，因此它对较小的倾向评分并不敏感。研究表明在所有的平衡权重中，重叠权重具有最小的渐近方差。
本节参考：
基于潜在结果框架的因果推断入门
3.4 重加权方法二：混杂因子平衡
这个方法很少见，有的观察变量都是混杂因子，有些变量可能是只影响结果的「调整变量」（adjustment variables），有些则可能是「无关变量」（irrelevant variables）。下图给出了关于混杂因子与调整变量的区别说明（这里并没有考虑到仅影响干预分配的工具变量以及介于干预与结果之间的中介变量）：
为了区分混杂因子与调整变量的不同影响，同时消除无关变量，研究者们提出了一种「数据驱动的可变性分解」算法（Data-Driven Variable Decomposition），调整后的结果通过下式给出：
所有的观察变量对
Y
∗
Y*
Y∗进行回归分析。该分析的目标函数是
Y
∗
Y*
Y∗ 与所有观察变量的线性回归函数的
l
2
l2
l2损失，以及用于区分混杂因子、调整变量与无关变量的稀疏正则项（注意这里本质上还是人工区分）。
然而，在实践中通常缺少关于观察变量的先验知识，同时数据通常是高维且包含噪声的。为了解决这一问题，研究者们又提出了「差分混杂因子平衡」（DCB）算法来从高维数据中选择并区分混杂因子，然后通过对样本与混杂因子同时进行重加权来平衡分布。
3.5 匹配方法：很常见
匹配的方法还是从选择偏差，CIA假定出发，进行修复，可以非常好的跟上RCT的实验思路。
Matching是一个非常经典发展历程也很长，且在很多领域比如政治经济社会医学等非常核心的方法，其思想淳朴但是底层逻辑稳固。
一个完整的问题建模基本从两个角度入手，一个是样本角度，一个是目标角度，matching完美从样本角度入手，使研究者正式treatment exposure和样本稀疏性问题（实干家）！
基于匹配的方法提供了一种估计反事实结果的方式，同时还能够减少混杂因子带来的偏差。一般来说，通过匹配方法给出第i个单元的潜在结果为：
对匹配样本的分析实际上是一种 RCT 的模仿：在 RCT 中，理想情况下干预组与对照组中协变量的分布是类似的，因此我们可以直接比较两个组之间的结果。匹配方法也是基于这样的思想来减少或消除混杂因子的影响。
核心要义，就是为每个实验组（T=1）样本，找到一个相近的对照组（T=0）
那么这里找、匹配的方法就是非常多了：
- 第一种：最给力+科学的 当然是，利用PS倾向性得分，直接用欧式距离进行计算，那么这里，PS + Matching联合的模型，PSM，就是更好的结合体，详情可见：
因果推断笔记——python 倾向性匹配PSM实现示例（三） - 第二种：利用一些用户属性信息，找到T=1下，用户属性比较接近的T=0的人群
在定义了相似度度量方式后，下一步就是找出相似的邻居。
现有的匹配算法可以被分为四类：最近邻匹配、卡钳匹配、分层匹配与核匹配。
上图对经典的距离度量与匹配算法进行了总结。
最常用的匹配算法是「最近邻匹配」（NNM），具体的步骤是基于相似度得分（例如倾向评分）选择对照组和干预组中最接近的单元进行匹配，干预组单元可以和一个对照组单元进行匹配，称为成对匹配或 1-1 匹配；也可以匹配到两个对照组，称为 1-2 匹配，以此类推。
邻居数量的选择是一个权衡，高数量的邻居可能会导致干预效果估计器的高偏差与低方差，而低数量的邻居会导致低偏差与高方差。
实际上最佳的结构应该是完全匹配的方式，即一个干预组可能对应多个对照组，而一个对照组可能对应一个或多个干预组。
此外，NNM 存在多种变体，如可重置的 NNM（可重复匹配）与不重置的 NNM。
3.6 Double Machine Learning (DML) / 回归
上面matching提到了从样本角度入手分析问题（causal graph上既focus on T），而从目标角度则是regression（causal graph上既focus on Y），（adjusting for all other causes of the outcome Y）限于篇幅太长，regression下次有机会再说。
regression进行估计存在一个问题是，对其他变量W估计有偏，则估计T的ATE存在偏差。
DML则是在进行HTE (Heterogenous Treatment Effect)研究中，通过残差估计矩(服从Neyman orthogonality)，即使W估计有偏，依旧可以得到无偏ATE估计！
训练的过程：
直观角度上，这里对回归比较熟悉的朋友可以知道，线性回归是拟合Y在特征空间X的最佳投影（既误差最小化），所以残差是垂直样本空间X的，既最大限度消除了（独立）X的相关性！如下图所示。
3.7 「元学习方法」（Meta-learning methods）
我们之前一直以ATE为例，实际观测数据中我们经常估计conditional ATE (CATE)，有些研究可能只关注treatment或者control组的ATE，分别叫ATT和ATC（有些情况下ATE无法估计）
该系列方法默认假定unconfoundedness（CIA假定） & positivity（正值假设）
而且，该方法是需要设立实验组treatment与对照组control的。
3.7.1 Conditional Outcome Modeling （COM） / S-learner
基于之前讨论我们得到ATE的识别为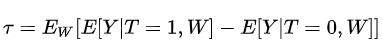
右边式子只包含statistical quantities，是statistical estimand。estimation需要我们用data估计estimate。最直接的办法就是我们可以先使用statistical model或者ML model估计conditional expectation，之后进行样本估计。
这里的估计，在实践看来其实就是利用模型的预测值
存在问题：当数据纬度变大时，容易产生估计偏差 (estimate biased towards 0！），这个很直观，假设数据有100维，T只是其中1维，模型训练时容易忽略这个维度，导致计算出来ATE -> 0，进而引出Grouped COM。
简单来看就是：
C A T E = ( Y . p r e d ∣ T = 1 , W , X ) − ( Y . p r e d ∣ T = 0 , W , X ) CATE = (Y.pred|T=1,W,X) - (Y.pred|T=0,W,X) CATE=(Y.pred∣T=1,W,X)−(Y.pred∣T=0,W,X)
这里的y.pred就是模型的预测值。
3.7.2 Grouped COM (GCOM) / T-Learner
GCOM引入为了解决COM中estimate biased towards to 0的问题，为了加强模型对T的权重，我们在估计 u u u时，分别对treatment组和control组使用不同的模型，其他流程与COM一样，也常叫T-Learner。
存在问题：每个estimator只使用部分数据，尤其当样本不足或者treatment、control样本量差别较大时，模型variance较大（对数据利用效率低），我们需要提升数据利用率！进而引出接下来2个model TARNet和X-Learner。
简单来看，这里会构建两个模型，treatment / control 两个：
C A T E = ( Y . p r e d 1 ∣ T = 1 , W , X ) − ( Y . p r e d 2 ∣ T = 0 , W , X ) CATE = (Y.pred1 |T=1,W,X) - (Y.pred2|T=0,W,X) CATE=(Y.pred1∣T=1,W,X)−(Y.pred2∣T=0,W,X)
这里的 y . p r e d 1 y.pred1 y.pred1就是模型1treatment的预测值, y . p r e d 2 y.pred2 y.pred2就是模型2control的预测值。
3.7.3 X-Learner
充分利用数据估计每个group的estimator，对于数据倾斜很严重的估计有很好的弥补作用。X-learner估计步骤如下：
简单来看，这里同样会构建两个模型，treatment / control 两个：
C A T E = [ ( Y . t r u e 1 ∣ T = 1 , W , X ) − ( Y . p r e d 1 ∣ T = 1 , W , X ) ] − [ ( Y . t r u e 2 ∣ T = 0 , W , X ) − ( Y . p r e d 2 ∣ T = 0 , W , X ) ] CATE = [(Y.true1 |T=1,W,X) - (Y.pred1|T=1,W,X)]-[(Y.true2 |T=0,W,X) - (Y.pred2|T=0,W,X)] CATE=[(Y.true1∣T=1,W,X)−(Y.pred1∣T=1,W,X)]−[(Y.true2∣T=0,W,X)−(Y.pred2∣T=0,W,X)]
这里的 y . p r e d 1 y.pred1 y.pred1就是模型1treatment的预测值与实际值，, y . p r e d 2 y.pred2 y.pred2就是模型2control的预测值与实际值。
3.8 Doubly Robust Methods - DRM
简单回顾一下刚介绍的方法，COM是预估Conditional Expectation u ( t , w ) u(t,w) u(t,w) ，IPW是预估propensity score e ( W ) e(W) e(W)。结合之前介绍的propensity score theorem，很自然可以同时预估2个量，并把 e ( W ) e(W) 因果推断笔记——工具变量内生性以及DeepIV