因果推断笔记——工具变量内生性以及DeepIV

Posted 2021-12-11 悟乙己

文章目录

• 1 理论介绍
• • 1.1 Instrumental variable解释
  • 1.2 因果推断中：内生性的一个有意思的例子
  • 1.2 与代理变量（proxy variable）的对比
  • 1.3 中介变量/mediation
  • 1.4 连玉君老师的简易解读
• 2 econML实现 DeepIV

---

同系列可参考：
因果推断笔记——因果图建模之微软开源的dowhy（一）
因果推断笔记—— 相关理论：Rubin Potential、Pearl、倾向性得分、与机器学习异同（二）
因果推断笔记——python 倾向性匹配PSM实现示例（三）
因果推断笔记——双重差分理论、假设、实践（四）
因果推断笔记——因果图建模之微软开源的EconML（五）
因果推断笔记——工具变量、内生性以及DeepIV（六）

---

1 理论介绍

参考：【统计】Instrumental Variables

exogenous - 外生性
endogenous - 内生性

1.1 Instrumental variable解释

线性模型前面的系数表征了自变量对于因变量的因果关系，一个线性模型要能使用 OLS 估计系数需要满足 exogeneity 的要求。现在假设其中某一个变量不满足该要求，即

这时，我们引入 instrumental variable 方法来解决内生性问题。

1.2 因果推断中：内生性的一个有意思的例子

考虑研究航空公司票价（prince，p）和销量（sales，y）的影响，即当其他条件不变时，如果增加票价，销量会如何变化；这是在研究一个 causal effect。

最好的方法就是随机化地做实验，比如随机对一些顾客，提高或者降低面向他们的票价；
但是这样的实验不仅会对航空公司造成实际的经济损失（损失了潜在的客户或者减少了盈利），而且还客户还因为不公平的对待而对航空公司不满。

因此，我们希望从历史数据里面来挖掘票价（P）和销量（Y）之间的因果关系：

• Confounders：一个直接的方法就是把 Y 对 P 做回归，但是这样往往得出错误的结论。比如可能存在另外的因素，节假日（X），它不仅影响票价（P）也同时影响销量（Y），在节假日的时候航空公司定价高（P 大），同时人们出行需求也大，因此销量也高（Y 大）；这是在历史数据里面做回归，得出的结论就会使 Y 和 P 成正相关，这显然是错误的。
• Unobservable variables：有一种方法是把可以观察到的影响因素也放到回归方程里面，根据前面几个 post 的内容，如果能够把所有的因素都包含进来，那么也能够得出正确的结论。但是，有可能会有一些观察不到的作用因素（E），比如在某个地区召开某个会议，它会同时使得票价（P）和销量（Y）都变大。
• Instrumental variable（IV）：因此，最有效的办法就是找到一个 IV，使得它只影响票价（当然，它也可以通过 P 来影响 Y，但是不能直接影响 Y），而和其他因素（X、E）不相关。
  在这里，我们找到 『燃油价格』这个因素来做为 IV，它上升时，航空公司基于成本考虑会上调票价 ，但是该因素和其他因素（比如是否节假日、是否在某个地区有会议）无关。需要注意的是，IV 的选取基本上基于人为的先验知识。

1.2 与代理变量（proxy variable）的对比

第一项的要求应该两个是等价的，即额外选择的这个变量不能成为解释变量进入原来的方程中。最主要的区别在第二个要求上，proxy variable 要求找到的变量能够解释所有 q 和其他 解释变量的关联（即，q 剔除掉 z 的影响之后，r 和其他解释变量无关）；而 instrumental variable 则希望找到一个和其他变量都没啥关系，但是只和 [公式] 有一点关联的变量。

论坛 (StackExchange)上说：instrumental variable 的目的是想找因果关系，减小 estimation error 产生的影响，对于它来说，$Xk$ 能观察到，但是可能有偏差，因此要找一个只影响$Xk$的变量来抵消相应的估计误差；
proxy variable是想想办法把原来的线性模型系数估计处理，其中的变量 q 观察不到，想要找一个和它接近的变量来替换它。

1个IV变量的估计：

用多个 Instrumental variable需要使用2SLS（ two-stage least square）：

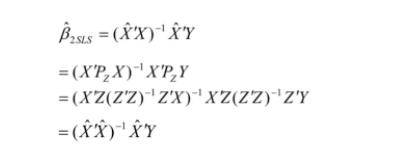
1.3 中介变量/mediation

参考：
因果推理初探（6）——干预工具（下）

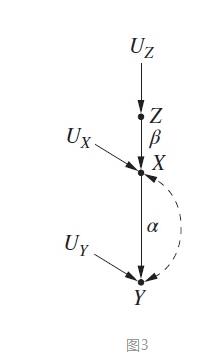
1.4 连玉君老师的简易解读

有哪些有趣的工具变量?

这是一种处理内生性问题的经典方法，或者说被滥用最严重的方法。这种方法相信大家都已经学过，就是找到一个变量和内生解释变量相关，但是和随机扰动项不相关。
在OLS的框架下同时有多个工具变量（IV），这些工具变量被称为two stage least squares (2SLS) estimator。具体的说，这种方法是找到影响内生变量的外生变量，连同其他已有的外生变量一起回归，得到内生变量的估计值，以此作为IV，放到原来的回归方程中进行回归。

工具变量法最大的问题是满足研究条件的工具变量难以找到，而不合乎条件的工具变量只能带来更严重的估计问题。

这里借用连玉君 的讲义

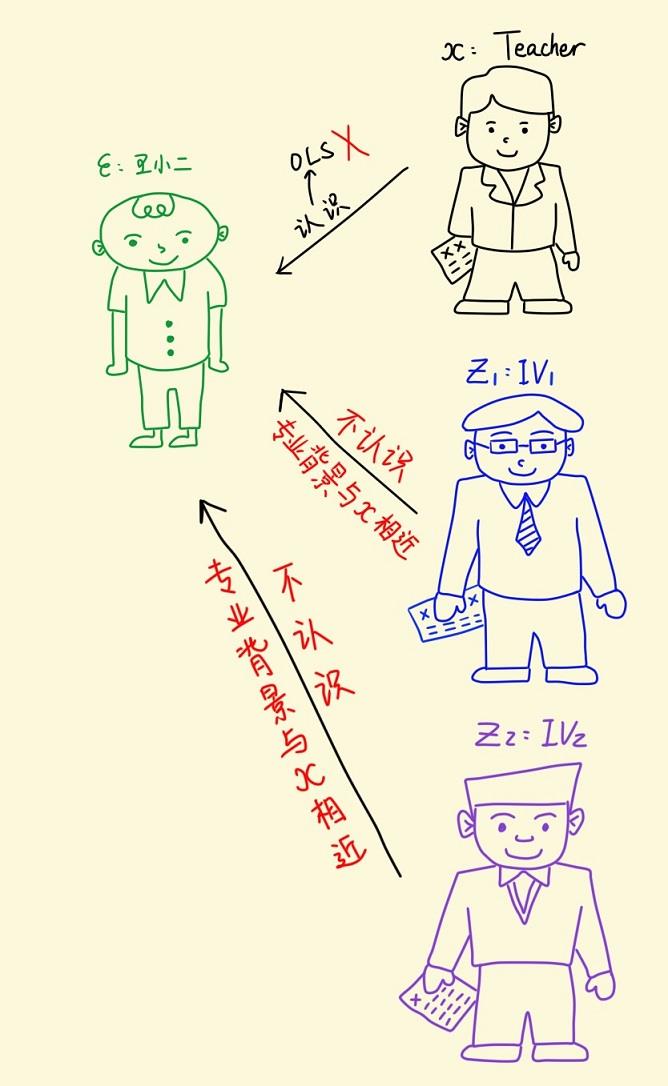
王小二参加研究生复试的面试时，恰好认识其中一位参加面试的老师。假设面试分数 (Y) 由面试老师 (X) 决定，王小二可视为随机误差项u ，认识王小二的那位面试老师可视为内生的解释变量x1 ，如果让这位老师继续参加面试给王小二打分，那么面试分数就很可能偏高。

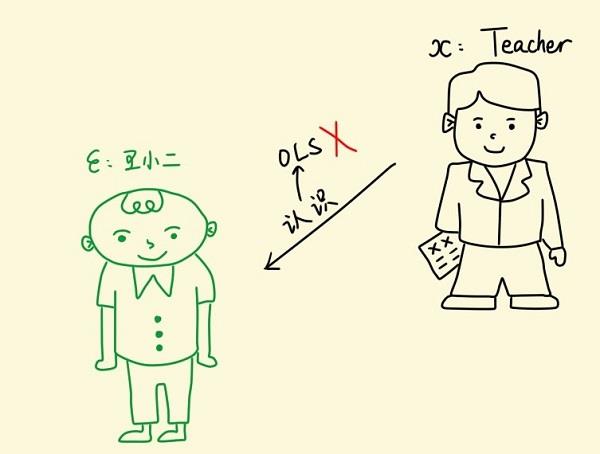
如何解决这个内生性问题呢？不妨再找另一个老师来代替这位跟王小二认识的老师，基本要求是：新找来的老师不能跟王小二认识，并且又跟被替换下的这位老师在专业背景方面有很高的相似度。这个新找来的老师就称为被替换下的老师的工具变量 (Instrumental Variable，简称 IV) 。接下来，让我们一起学习 IV 估计。

如果 “王小二面试” 时找来一个代替老师，那么这位新老师给的面试分数还是有一定的随机性，一个主要的原因是新找来的这位老师可能与被替换的那位老师之间的相关性不够强。为了控制面试得分偏差，我们可以多找几个老师。不妨再找一个老师，这两个老师就称为被替换下来的老师的两个工具变量。

2 econML实现 DeepIV

DeepIV 可以看做把上述 2SLS 方法推广到非线性模型。
论文参考：Deep IV: A Flexible Approach for Counterfactual Prediction
DeepIV 结构可参考：【统计】Instrumental Variables

代码：DeepIV examples

Deep IV 需要设定的变量:

• Covariates, 协变量，which we will denote with X
• Instruments, 工具变量，which we will denote with Z
• Treatments, 干预，which we will denote with T
• Responses, 因变量，which we will denote with Y

主要要求是Z是一组有效的工具，且只能通过T，作用Y，不能直接作用Y。
Deep IV估计器会拟合两个模型：

• treatment model（T|Z,X） 干预模型（工具变量Z -> 干预T）：It estimates the distribution of the treatment T given Z and X, using a mixture density network.
• response model （Y|T,X）响应模型(干预T -> 因变量Y)： It estimates the dependence of the response Y on T and X.

代码：

from econml.iv.nnet import DeepIV
import keras
import numpy as np
import matplotlib.pyplot as plt

%matplotlib inline

n = 5000

# Initialize exogenous variables; normal errors, uniformly distributed covariates and instruments
e = np.random.normal(size=(n,))
x = np.random.uniform(low=0.0, high=10.0, size=(n,))
z = np.random.uniform(low=0.0, high=10.0, size=(n,))

# Initialize treatment variable
t = np.sqrt((x+2) * z) + e

# Show the marginal distribution of t
plt.hist(t)
plt.xlabel("t")
plt.show()

plt.scatter(z[x < 1], t[x < 1], label='low X')
plt.scatter(z[(x > 4.5) * (x < 5.5)], t[(x > 4.5) * (x < 5.5)], label='moderate X')
plt.scatter(z[x > 9], t[x > 9], label='high X')
plt.legend()
plt.xlabel("z")
plt.ylabel("t")
plt.show()

# 构建模型
treatment_model = keras.Sequential([keras.layers.Dense(128, activation='relu', input_shape=(2,)),
                                    keras.layers.Dropout(0.17),
                                    keras.layers.Dense(64, activation='relu'),
                                    keras.layers.Dropout(0.17),
                                    keras.layers.Dense(32, activation='relu'),
                                    keras.layers.Dropout(0.17)])

response_model = keras.Sequential([keras.layers.Dense(128, activation='relu', input_shape=(2,)),
                                   keras.layers.Dropout(0.17),
                                   keras.layers.Dense(64, activation='relu'),
                                   keras.layers.Dropout(0.17),
                                   keras.layers.Dense(32, activation='relu'),
                                   keras.layers.Dropout(0.17),
                                   keras.layers.Dense(1)])

# deepIV模型初始化
keras_fit_options = { "epochs": 30,
                      "validation_split": 0.1,
                      "callbacks": [keras.callbacks.EarlyStopping(patience=2, restore_best_weights=True)]}

deepIvEst = DeepIV(n_components = 10, # number of gaussians in our mixture density network
                   m = lambda z, x : treatment_model(keras.layers.concatenate([z,x])), # treatment model
                   h = lambda t, x : response_model(keras.layers.concatenate([t,x])),  # response model
                   n_samples = 1, # number of samples to use to estimate the response
                   use_upper_bound_loss = False, # whether to use an approximation to the true loss
                   n_gradient_samples = 1, # number of samples to use in second estimate of the response (to make loss estimate unbiased)
                   optimizer='adam', # Keras optimizer to use for training - see https://keras.io/optimizers/ 
                   first_stage_options = keras_fit_options, # options for training treatment model
                   second_stage_options = keras_fit_options) # options for training response model

# 模型fit
deepIvEst.fit(Y=y,T=t,X=x,Z=z)

来看一下预测：

n_test = 500
for i, x in enumerate([1,2,3,5,8,10]):
    t = np.linspace(0,10,num = 100)
    y_true = t*t / 10 - x*t/10
    y_pred = deepIvEst.predict(t, np.full_like(t, x))
    plt.plot(t, y_true, label='true y, x={0}'.format(x),color='C'+str(i))
    plt.plot(t, y_pred, label='pred y, x={0}'.format(x),color='C'+str(i),ls='--')
plt.xlabel('t')
plt.ylabel('y')
plt.legend()
plt.show()

你可以看到，尽管响应面随x变化，但我们的模型能够很好地拟合数据。
在低x的情况下，仪器的功率最小。
在这里，它适合一条直线而不是二次曲线，这表明正则化至少表现得很好。